정렬
👉 정렬: 데이터를 순서대로 나열하는 방법
버블 정렬
첫 번째 자료와 두 번째 자료를, 두 번째 자료와 세 번째 자료를, 세 번째 자료와 네 번째 자료를, ... 이런 식으로 (n-1)번 째 자료와 마지막 자료를 비교하여 교환하면서 정렬하는 방식
작은 숫자, 큰 숫자 순서로 있으면 내버려 두고
큰 숫자, 작은 숫자 순서로 있으면 둘의 위치를 바꾼다
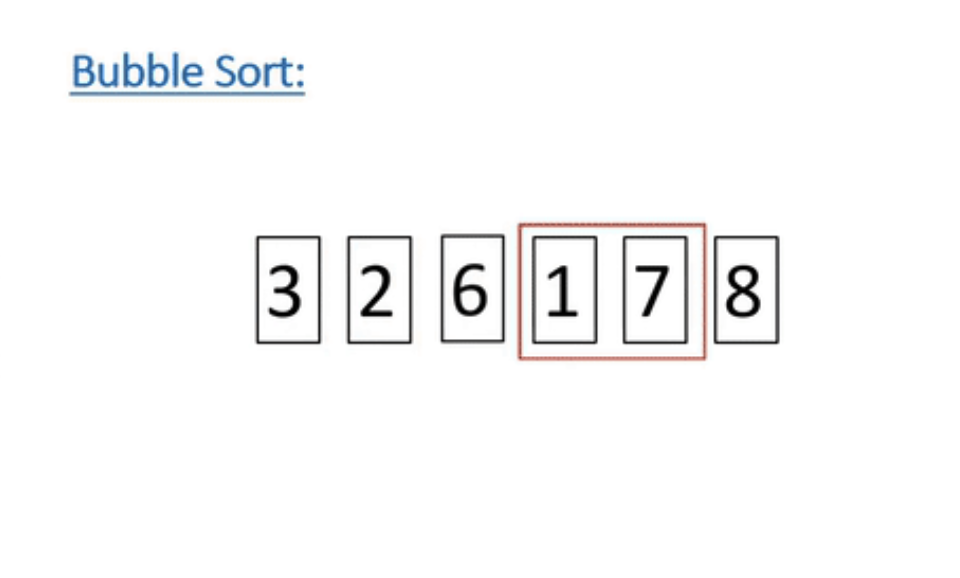
[4, 6, 2, 9, 1] # 정렬되지 않은 배열
1단계 : [4, 6, 2, 9, 1]
4와 6을 비교
4 < 6 이면 그대로 둔다
2단계 : [4, 6, 2, 9, 1]
6과 2를 비교
6 > 2 이므로 둘을 변경
[4, 2, 6, 9, 1]
3단계 : [4, 2, 6, 9, 1]
6과 9를 비교
6 < 9 이면 그대로 둔다
4단계 : [4, 2, 6, 9, 1]
9와 1를 비교
9 > 1 이므로 둘을 변경
[4, 2, 6, 1, 9]
5단계 : [4, 2, 6, 1, 9]
4와 2을 비교
4 > 2 이므로 둘을 변경
[2, 4, 6, 1, 9]
6단계 : [2, 4, 6, 1, 9]
4와 6을 비교
4 < 6 이면 그대로 둔다
7단계 : [2, 4, 6, 1, 9]
6와 1을 비교
6 > 1 이므로 둘을 변경
[2, 4, 1, 6, 9]
8단계 : [2, 4, 1, 6, 9]
2와 4을 비교
2 < 4 이면 그대로 둔다
9단계 : [2, 4, 1, 6, 9]
4와 1을 비교
4 > 1 이므로 둘을 변경
[2, 1, 4, 6, 9]
10단계 : [2, 1, 4, 6, 9]
2와 1을 비교
2 > 1 이므로 둘을 변경
[1, 2, 4, 6, 9] 이를 코드로 나타내려면
- array[j] > array[j + 1] 라면 두 값을 변경
input = [4, 6, 2, 9, 1]
def bubble_sort(array):
n = len(array)
for i in range(n):
for j in range(n - i - 1):
if array[j] > array[j+1]:
array[j], array[j+1] = array[j+1], array[j]
return array
bubble_sort(input)
print(input) # [1, 2, 4, 6, 9] 가 되어야 합니다!
print("정답 = [1, 2, 4, 6, 9] / 현재 풀이 값 = ",bubble_sort([4, 6, 2, 9, 1]))
print("정답 = [-1, 3, 9, 17] / 현재 풀이 값 = ",bubble_sort([3,-1,17,9]))
print("정답 = [-3, 32, 44, 56, 100] / 현재 풀이 값 = ",bubble_sort([100,56,-3,32,44]))❓ Q. 이 함수의 시간 복잡도는?
✅ 만큼 걸린다. 함수 구문 하나하나를 보지 않더라도, 2차 반복문이 나왔고, array 의 길이 만큼 반복한다면
선택 정렬
: 선택해서 정렬한다.
예) 사람들이 일렬로 서 있을 때, 가장 키가 작은 사람을 찾아 맨 앞에 두기. 그 다음, 다시 한 번 더 둘러보면서 두 번째로 작은 사람을 두 번째에 배치.
[4, 6, 2, 9, 1] # 정렬되지 않은 배열
1단계 : [4, 6, 2, 9, 1]
4와 6과 2와 9와 1을 차례차례 비교
그 중 가장 작은 1과 맨 앞 자리인 4를 교체
[1, 6, 2, 9, 4]
그러면, 맨 앞자리를 제외하고 다시 한 번 반복
2단계 : [1, 6, 2, 9, 4]
6과 2와 9와 4를 차례차례 비교
그 중 가장 작은 2와 두번째 앞 자리인 6을 교체
[1, 2, 6, 9, 4]
3단계 : [1, 2, 6, 9, 4]
6과 9와 4를 차례차례 비교
그 중 가장 작은 4와 세번째 앞 자리인 6을 교체
[1, 2, 4, 9, 6]
4단계 : [1, 2, 4, 9, 6]
9와 6을 비교
그 중 가장 작은 6과 네번째 앞 자리인 9을 교체
[1, 2, 4, 6, 9] 이를 코드로 나타내려면

즉, 배열의 크기만큼 반복했다가, 앞에서부터 1개씩 줄어들면서 반복한다
✅ 버블 정렬하고 다른 건 바로 "최솟값"을 찾아 변경하는 것. 따라서, min_index 라는 변수를 통해 각각의 인덱스들과 비교한다. 그리고 내부의 반복문이 끝나면, 최소 값의 인덱스와 i의 값들을 교체한다.
input = [4, 6, 2, 9, 1]
def selection_sort(array):
n = len(array)
for i in range(n-1):
min_index = i
for j in range(n-i):
if array[i+j] < array[min_index]:
min_index = i + j
array[i], array[min_index] = array[min_index], array[i]
return array
selection_sort(input)
print(input) # [1, 2, 4, 6, 9] 가 되어야 합니다!
print("정답 = [1, 2, 4, 6, 9] / 현재 풀이 값 = ",selection_sort([4, 6, 2, 9, 1]))
print("정답 = [-1, 3, 9, 17] / 현재 풀이 값 = ",selection_sort([3,-1,17,9]))
print("정답 = [-3, 32, 44, 56, 100] / 현재 풀이 값 = ",selection_sort([100,56,-3,32,44]))❓ Q. 여기서 퀴즈, 이 함수의 시간 복잡도는?
✅
삽입 정렬
👉 선택 정렬리 전체에서 최솟값을 "선택"하는 것이였다면, 삽입 정렬은 전체에서 하나씩 올바른 위치에 "삽입"하는 방식이다. 선택 정렬은 현재 데이터의 상태와 상관없이 항상 비교하고 위치를 바꾸지만, 삽입 정렬은 필요할 때만 위치를 변경하므로 더 효율적인 방식이다.
예를 들어
이미 키 순으로 정렬된 사람들이 일렬로 쭉 서있을 때 다음 원소가 그 정렬된 사람들 사이를 비집고 들어가면서 삽입하며 정렬하는 방식.
[4, 6, 2, 9, 1] # 정렬되지 않은 배열
1단계 : [4, 6, 2, 9, 1]
4는 현재 정렬되어 있는 부대원
그럼 이제 새로운 신병인 6을 받음
4, 6 이 되는데 4 < 6 이므로 그대로 둔다
[4, 6, 2, 9, 1!
이 과정에서 새로운 부대원인 4, 6은 현재 정렬된 상태.
이처럼, 삽입 정렬은 한 바퀴가 돌 때마다 정렬된 상태가 된다.
2단계 : [4, 6, 2, 9, 1]
4, 6 은 현재 정렬되어 있는 부대원
그럼 이제 새로운 신병인 2를 받음
4, 6, 2 가 되는데 6 > 2 이므로 둘을 변경
4, 2, 6 가 되는데 4 > 2 이므로 둘을 변경
[2, 4, 6, 9, 1]
3단계 : [2, 4, 6, 9, 1]
2, 4, 6 은 현재 정렬되어 있는 부대원
그럼 이제 새로운 신병인 9를 받음
2, 4, 6, 9 가 되는데 6 < 9 이므로 그대로 둔다.
[2, 4, 6, 9, 1]
4단계 : [2, 4, 6, 9, 1]
2, 4, 6, 9 은 현재 정렬되어 있는 부대원
그럼 이제 새로운 신병인 1을 받음
2, 4, 6, 9, 1 가 되는데 9 > 1 이므로 둘을 변경
2, 4, 6, 1, 9 가 되는데 6 > 1 이므로 둘을 변경
2, 4, 1, 6, 9 가 되는데 4 > 1 이므로 둘을 변경
2, 1, 4, 6, 9 가 되는데 2 > 1 이므로 둘을 변경
[1, 2, 4, 6, 9] 이를 코드로 옮기러면

즉, 1만큼 비교했다가 1개씩 늘어나면서 반복한다.
input = [4, 6, 2, 9, 1]
def insertion_sort(array):
n = len(array)
for i in range(1, n):
for j in range(i):
if array[i-j-1] > array[i-j]:
array[i-j-1], array[i-j] = array[i-j], array[i-j-1]
else:
break
insertion_sort(input)
print(input) # [1, 2, 4, 6, 9] 가 되어야 합니다!
print("정답 = [4, 5, 7, 7, 8] / 현재 풀이 값 = ",insertion_sort([5,8,4,7,7]))
print("정답 = [-1, 3, 9, 17] / 현재 풀이 값 = ",insertion_sort([3,-1,17,9]))
print("정답 = [-3, 32, 44, 56, 100] / 현재 풀이 값 = ",insertion_sort([100,56,-3,32,44]))❓ Q. 여기서 퀴즈, 이 함수의 시간 복잡도는?
✅
그러나, 버블 정렬과 선택 정렬과 다른 면이 있다.
버블 정렬과 선택 정렬은 최선이든 최악이든 항상 만큼의 시간이 걸렸지만,
최선의 경우에는 만큼의 시간 복잡도가 걸립니다.
거의 정렬이 된 배열이 들어간다면 break 문에 의해서
더 많은 원소와 비교하지 않고 탈출할 수 있기 때문이다.
병합 정렬 - merge
👉 병합 정렬은 배열의 앞부분과 뒷부분의 두 그룹으로 나누어 각각 정렬한 후 병합하는 작업을 반복하는 알고리즘이다. 예를 들어 A라고 하는 배열이 1,2,3,5로 정렬되어 있고, B라는 배열이 4,6,7,8로 정렬되어 있다면 이 두 집합을 합쳐가면서 정렬하는 방법이다.
- 정렬된 배열을 합치는 것
[1, 2, 3, 5] # 정렬된 배열 A
[4, 6, 7, 8] # 정렬된 배열 B
[] # 두 집합을 합칠 빈 배열 C
↓
1단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
1과 4를 비교
1 < 4 이므로 1을 C 에 넣음
C:[1]
↓
2단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
2와 4를 비교
2 < 4 이므로 2를 C 에 넣음
C:[1, 2]
↓
3단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
3과 4를 비교
3 < 4 이므로 3을 C 에 넣음
C:[1, 2, 3]
↓
3단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
5와 4를 비교
5 > 4 이므로 4을 C 에 넣음
C:[1, 2, 3, 4]
↓
3단계 : [1, 2, 3, 5]
↓
[4, 6, 7, 8]
5와 6을 비교
5 < 6 이므로 5을 C 에 넣음
C:[1, 2, 3, 4, 5]
A 원소 종료
여기서 B에서 안 들어간 원소인
[6, 7, 8] 은
하나씩 C 에 추가한다.
C:[1, 2, 3, 4, 5, 6, 7, 8] ✅ 두 개의 배열을 합치기 위해서는 각 배열의 값들을 하나씩 비교한다. 그리고 더 작은 값을 새로운 배열에 하나씩 추가한다. 한 배열이 끝나면 남은 배열의 모든 값을 새로운 배열에 추가한다. 그리거 위해서서 result라는 새로운 배열을 만든 다음에 다음과 같이 while 문을 이용해 비교 이후에 값을 추가한다.
array_a = [1, 2, 3, 5]
array_b = [4, 6, 7, 8]
def merge(array1, array2):
result=[]
array1_index = 0
array2_index = 0
while array1_index < len(array1) and array2_index < len(array2):
if array1[array1_index] < array2[array2_index]:
result.append(array1[array1_index])
array1_index += 1
else:
result.append(array2[array2_index])
array2_index += 1
if array1_index == len(array1):
while array2_index < len(array2):
result.append(array2[array2_index])
array2_index += 1
if array2_index == len(array2):
while array1_index < len(array1):
result.append(array1[array1_index])
array1_index += 1
return result
print(merge(array_a, array_b)) # [1, 2, 3, 4, 5, 6, 7, 8] 가 되어야 합니다!
print("정답 = [-7, -1, 5, 6, 9, 10, 11, 40] / 현재 풀이 값 = ", merge([-7, -1, 9, 40], [5, 6, 10, 11]))
print("정답 = [-1, 2, 3, 5, 10, 40, 78, 100] / 현재 풀이 값 = ", merge([-1,2,3,5,40], [10,78,100]))
print("정답 = [-1, -1, 0, 1, 6, 9, 10] / 현재 풀이 값 = ", merge([-1,-1,0], [1, 6, 9, 10]))병합 정렬 - mergeSort
👉 분할 정복은 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다. 예를 들어 [5, 3, 2, 1, 6, 8, 7, 4] 이라는 배열이 있다고 하자.
이 배열을 반으로 쪼개면 [5, 3, 2, 1][6, 8, 7, 4] 이 된다.
또 반으로 쪼개면 [5, 3][2, 1] [6, 8][7, 4] 이 되고,
또 반으로 쪼개면[5][3] [2][1] [6][8] [7][4] 이 된다.
이 배열들을 두개씩 병합을 하면 어떻게 될까?
[5][3] 을 병합하면 [3, 5] 로
[2][1] 을 병합하면 [1, 2] 로
[6][8] 을 병합하면 [6, 8] 로
[7][4] 을 병합하면 [4, 7] 로
그러면 다시
[3, 5] 과 [1, 2]을 병합하면 [1, 2, 3, 5] 로
[6, 8] 와 [4, 7]을 병합하면 [4, 6, 7, 8] 로
그리고 다시
[1, 2, 3, 5] 과 [4, 6, 7, 8] 를 병합하면 [1, 2, 3, 4, 5, 6, 7, 8] 이 된다.
이를 분할 정복(Divide and Conquer)라고 한다
✅ 이렇게 동일한 형태로 반복되는 경우는 재귀적인 코드에 해당한다.
자기 자신을 포함하는 형식으로 함수를 이용해서 정의해보면,
MergeSort(시작점, 끝점) 이라고 할 수 있다.
그러면
MergeSort**(0, N)** = Merge(MergeSort**(0, N/2)** + MergeSort**(N/2, N)**)
라고 할 수 있습니다.
즉, 0부터 N까지 정렬한 걸 보기 위해서는
아까 봤던 [1, 2, 3, 5] 와 [4, 6, 7, 8] 을 합치면 정렬된 배열이 나온 것 처럼
0부터 N/2 까지 정렬한 것과 N/2부터 N까지 정렬한 걸 **합치면 된다.** 라는 개념입니다.🔥재귀 함수의 필수 조건(탈출 조건): 문자열의 길이가 1보다 작거나 같을 때
array = [5, 3, 2, 1, 6, 8, 7, 4]
def merge_sort(array):
if len(array) <=1:
return array
mid = len(array) //2
left_array = array[:mid]
right_array =array[mid:]
return merge(merge_sort(left_array),merge_sort(right_array))
def merge(array1, array2):
result = []
array1_index = 0
array2_index = 0
while array1_index < len(array1) and array2_index < len(array2):
if array1[array1_index] < array2[array2_index]:
result.append(array1[array1_index])
array1_index += 1
else:
result.append(array2[array2_index])
array2_index += 1
if array1_index == len(array1):
while array2_index < len(array2):
result.append(array2[array2_index])
array2_index += 1
if array2_index == len(array2):
while array1_index < len(array1):
result.append(array1[array1_index])
array1_index += 1
return result
print(merge_sort(array)) # [1, 2, 3, 4, 5, 6, 7, 8] 가 되어야 합니다!
print("정답 = [-7, -1, 5, 6, 9, 10, 11, 40] / 현재 풀이 값 = ", merge_sort([-7, -1, 9, 40, 5, 6, 10, 11]))
print("정답 = [-1, 2, 3, 5, 10, 40, 78, 100] / 현재 풀이 값 = ", merge_sort([-1, 2, 3, 5, 40, 10, 78, 100]))
print("정답 = [-1, -1, 0, 1, 6, 9, 10] / 현재 풀이 값 = ", merge_sort([-1, -1, 0, 1, 6, 9, 10]))✅ merge 함수 시간 복잡도
👉 while 문이 len(array1) 과 len(array2)의 길이 만큼 반복하고 있다.
즉, 최대 len(array1) + len(array2) 만큼의 연산량이 필요한데, 이의 최댓값은 O(N)이다.
왜냐면 array1과 array2 는 결국 array 를 반으로 잘라서 넣은 길이이기 때문이다.
따라서 merge 함수의 시간 복잡도는 O(N)이다.
✅ merge_sort 함수 시간 복잡도
👉 merge_sort 는 대입 연산과 비교 연산 몇 번밖에 나오지 않으므로 상수의 시간 복잡도를 가진다.
✅ 위의 케이스에서 봤듯이,
[1, 2, 3, 4, 5, 6, 7, 8] 을 정렬하기 위해
[1, 2, 3, 5] 과 [4, 6, 7, 8] 을 병합했다.
[1, 2, 3, 5] 과 [4, 6, 7, 8] 을 정렬하기 위해
[3, 5] [1, 2] 과 [6, 8] [4,7] 을 병합했다.
[3, 5] [1, 2] 과 [6, 8] [4,7] 을 정렬하기 위해
[5] [3] [2] [1] [6] [8] [7] [4] 를 병합했다.
이를 얼마나 시간이 걸리는지에 대한 관점으로 보면,
T(N) 을 N 의 길이를 정렬하기 위해 걸리는 시간이라고 하자.
**1단계**
[1, 2, 3, 4, 5, 6, 7, 8] 을 정렬하기 위해
[1, 2, 3, 5] 과 [4, 6, 7, 8] 을 병합했다.
즉, 크기 N 인 배열을 정렬하기 위해
크기 N/2 인 부분 배열 2개를 비교한다.
그러면 N/2 * 2 = N 번 비교하게 된다.
**2단계**
[1, 2, 3, 5] 과 [4, 6, 7, 8] 을 정렬하기 위해
[3, 5] [1, 2] 과 [6, 8] [4,7] 을 병합했다.
즉, 크기 N/2 인 부분 배열 2개를 정렬하기 위해
크기 N/4 인 부분 배열 4개를 비교한다.
그러면 N/4 * 4 = N 번 비교하게 된다.
**3단계**
[3, 5] [1, 2] 과 [6, 8] [4,7] 을 정렬하기 위해
[5] [3] [2] [1] [6] [8] [7] [4] 를 병합했다.
즉, 크기 N/4 인 부분 배열 4개를 정렬하기 위해
크기 N/8 인 부분 배열 8개를 비교한다.
그러면 N/8 * 2 = N 번 비교하게 된다.
즉 모든 단계에서 N 만큼 비교를 한다.
그러면 총 몇 단계인지만 알면 시간 복잡도를 구할 수 있다.
크기가 → → → → .... →
이 되는 순간이 있을텐테,이는 !로 표기할 수 있다.
바로 번 반복하게 되면 1이 된다.
이걸 수식으로 나타내면
N만큼의 연산을 logN 번 반복한다고 해서
시간 복잡도는 총 이 된다.
스택
📖 한쪽 끝으로만 자료를 넣고 뺄 수 있는 자료 구조. Last in, First out
스택의 구현
push(data): 맨 앞에 데이터 넣기
pop(): 맨 앞 데이터 뽑기
peek(): 맨 앞 데이터 보기
sEmpty(): 스택이 비었는지 안 비었는지 여부 반환해주기
스택은 데이터 넣고 뽑는 걸 자주하는 자료 구조.
링크드 리스트와 유사하게 구현할 수 있다 push - 맨 앞에 데이터 넣기
def push(self, value):
new_head = Node(value)
new_head.next = self.head
self.head = new_headpop - 맨 앞 데이터 뽑기
def pop(self):
if self.is_empty():
return "Stacj is empty"
delete_head = self.head
self.head = self.head.next
return delete_headpeek - 맨 앞 데이터 보기
def peek(self):
if self.is_empty():
return "Stack is empty!"
return self.head.datais_empty - 비어있는지 아닌지, head가 None인지 아닌지 여부를 반환
def is_empty(self):
return self.head is None예제)
top_heights = [6, 9, 5, 7, 4]
def get_receiver_top_orders(heights):
answer = [0] * len(heights)
while heights:
height = heights.pop()
for idx in range(len(heights) - 1, -1, -1):
if heights[idx] > height:
answer[len(heights)] = idx + 1
break
return answer
print(get_receiver_top_orders(top_heights)) # [0, 0, 2, 2, 4] 가 반환되어야 한다!
print("정답 = [0, 0, 2, 2, 4] / 현재 풀이 값 = ",get_receiver_top_orders([6,9,5,7,4]))
print("정답 = [0, 0, 0, 3, 3, 3, 6] / 현재 풀이 값 = ",get_receiver_top_orders([3,9,9,3,5,7,2]))
print("정답 = [0, 0, 2, 0, 0, 5, 6] / 현재 풀이 값 = ",get_receiver_top_orders([1,5,3,6,7,6,5]))큐
📖 한쪽 끝으로 자료를 넣고, 반대쪽에서는 자료를 뺄 수 있는 선형구조.First in, First out
👉 큐라는 자료 구조에서 제공하는 기능enqueue(data) : 맨 뒤에 데이터 추가하기
dequeue() : 맨 앞의 데이터 뽑기
peek() : 맨 앞의 데이터 보기
isEmpty(): 큐가 비었는지 안 비었는지 여부 반환해주기
스택과 다르게 큐는 끝과 시작의 노드를 전부 가지고 있어야 하므로,
self.head 와 self.tail 을 가지고 시작한다.
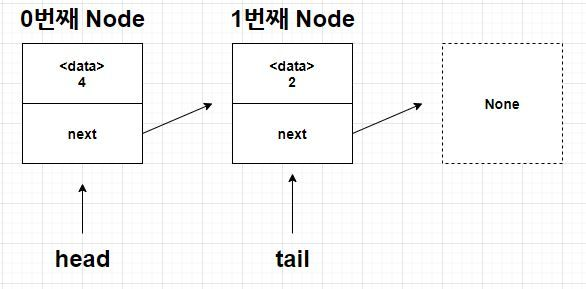
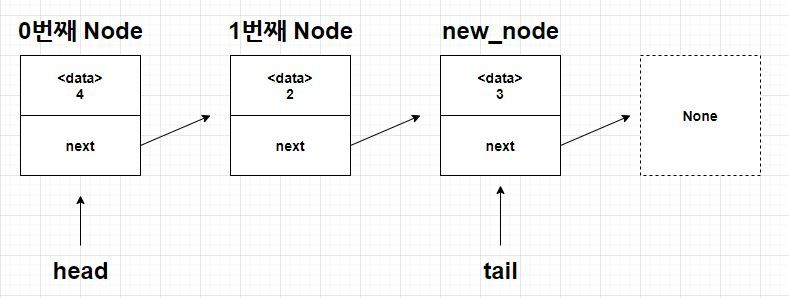
new_node = node(value) # [3] 을 만들고,
self.tail.next = new_node # 여기서 문제가 생긴다.
(self.tail 은 None 인데 next 를 하니까)
그래서, 빈 경우에는 예외적으로 처리를 해줘야 한다.
[3] 은 head 이자 tail 이 되도록 설정해줘야 한다.
class Node:
def __init__(self, data):
self.data = data
self.next = None
class Queue:
def __init__(self):
self.head = None
self.tail = None
def enqueue(self, value):
new_node = Node(value)
if self.is_empty(): # 만약 비어있다면,
self.head = new_node # head 에 new_node를
self.tail = new_node # tail 에 new_node를 넣어준다.
return
self.tail.next = new_node
self.tail = new_node
def dequeue(self):
if self.is_empty():
return "Queue is empty!" # 만약 비어있다면 에러!
delete_head = self.head # 제거할 node 를 변수에 잡습니다.
self.head = self.head.next # 그리고 head 를 현재 head 의 다음 걸로 잡으면 됩니다.
return delete_head.data # 그리고 제거할 node 반환
def peek(self):
if self.is_empty():
return "Queue is empty!"
return self.head.data
def is_empty(self):
return self.list.head is None해쉬 테이블
📖 컴퓨팅에서 키를 값에 매핑할 수 있는 구조인, 연관 배열 추가에 사용되는 자료 구조이다. 해시 테이블은 해시 함수를 사용하여 색인(index)을 버킷(bucket)이나 슬롯(slot)의 배열로 계산한다. 데이터를 다루는 기법 중에 하나로 데이터의 검색과 저장이 아주 빠르게 진행된다.
📖 해쉬 함수(Hash Function)는 임의의 길이를 갖는 메시지를 입력하여 고정된 길이의 해쉬값을 출력하는 함수이다
ex) 파이썬에서는 hash(object)로 해쉬함수 제공
>>> hash("fast")
-146084012848775433
>>> hash("slow")
7051061338400740146- 딕셔너리 함수
- put(key, value): key에 value 저장하기
- get(key): key에 해당하는 value 가져오기
put
def put(self, key, value):
index = hash(key) % len(self.items)
self.items[index] = valueget
def get(self, key):
index = hash(key) % len(self.items)
return self.items[index]🔥 만약 해쉬의 값이 같으면,혹은 해쉬 값을 배열의 길이로 나눴더니 똑같은 숫자가 되면 충돌(collision)이 발생한다 . 같은 어레이의 인덱스로 매핑이 되어서 데이터를 덮어 써버리는 것을 충돌이 발생했다고 한다.
✅ 충돌을 해결하는 첫번째 방법은 바로 링크드 리스트를 사용하는 방식이다.
이 방식을 연결지어서 해결한다고 해서 체이닝(Chaining) 이라고 한다.
두 번째 방식은 배열의 다음 남는 공간에 넣는 것이다. 이를 개방 주소법(Open Addressing)이라고 한다.
- 체이닝 방법
class LinkedDict:
def __init__(self):
self.items = []
for i in range(8):
self.items.append(LinkedTuple())
def put(self, key, value):
index = hash(key) % len(self.items)
self.items[index].add(key, value)
# 만약, 입력된 key가 "fast" 인데 index 값이 2가 나왔다.
# 현재 self.items[2] 가 [("slow", "느린")] 이었다!
# 그렇다면 새로 넣는 key, value 값을 뒤에 붙여주자!
# self.items[2] == [("slow", "느린") -> ("fast", "빠른")] 이렇게!
def get(self, key):
index = hash(key) % len(self.items)
return self.items[index].get(key)
# 만약, 입력된 key가 "fast" 인데 index 값이 2가 나왔다.
# 현재 self.items[2] 가 [("slow", "느린") -> ("fast", "빠른")] 이었다!
# 그렇다면 그 리스트를 돌면서 key 가 일치하는 튜플을 찾아준다.
# ("fast", "빠른") 이 일치하므로 "빠른" 이란 값을 돌려주자!👨🏫 해쉬 테이블(Hash Table)은 "키" 와 "데이터"를 저장함으로써 즉각적으로 데이터를 받아오고 업데이트하고 싶을 때 사용하는 자료구조이다.
해쉬 함수(Hash Function)는 임의의 길이를 갖는 메시지를 입력하여 고정된 길이의 해쉬값을 출력하는 함수이다. 해쉬 테이블의 내부 구현은 키를 해쉬 함수를 통해 임의의 값으로 변경한 뒤 배열의 인덱스로 변환하여 해당하는 값에 데이터를 저장한다.
그렇기 때문에 즉각적으로 데이터를 찾고, 추가할 수 있다.
만약, 해쉬 값 혹은 인덱스가 중복되어 충돌이 일어난다면
체이닝과 개방 주소법 방법으로 해결한다.
예제)
all_students = ["나연", "정연", "모모", "사나", "지효", "미나", "다현", "채영", "쯔위"]
present_students = ["정연", "모모", "채영", "쯔위", "사나", "나연", "미나", "다현"]
def get_absent_student(all_array, present_array):
dict = {}
for key in all_array:
dict[key] = True # 아무 값이나 넣어도 상관 없습니다! 여기서는 키가 중요한거니까요
for key in present_array: # dict에서 key 를 하나씩 없앱니다
del dict[key]
for key in dict.keys(): # key 중에 하나를 바로 반환합니다! 한 명 밖에 없으니 이렇게 해도 괜찮습니다.
return key
print(get_absent_student(all_students, present_students))
print("정답 = 예지 / 현재 풀이 값 = ",get_absent_student(["류진","예지","채령","리아","유나"],["리아","류진","채령","유나"]))
print("정답 = RM / 현재 풀이 값 = ",get_absent_student(["정국","진","뷔","슈가","지민","RM"],["뷔","정국","지민","진","슈가"]))
