파이썬 자료구조 4

원·2022년 9월 20일
TIL자료구조
0

TIL

목록 보기
11/46

트리

📖 뿌리와 가지로 구성되어 거꾸로 세워놓은 나무처럼 보이는 계층형 비선형 자료 구조

👉 큐(Queue), 스택(Stack)은 자료구조에서 선형구조라고 한다. 선형 구조란 자료를 구성하고 있는 데이터들을 순차적으로 나열한 형태를 의미한다. 트리는 비선형 구조로 비선형 구조는 선형 구조와 다르게 데이터가 계층적 혹은 망으로 구성되어있다

선형 구조는 자료를 저장하고 꺼내는 것에 초점이 맞춰져 있고, 비선형 구조는 표현에 초점이 맞춰져 있다

  • 트리

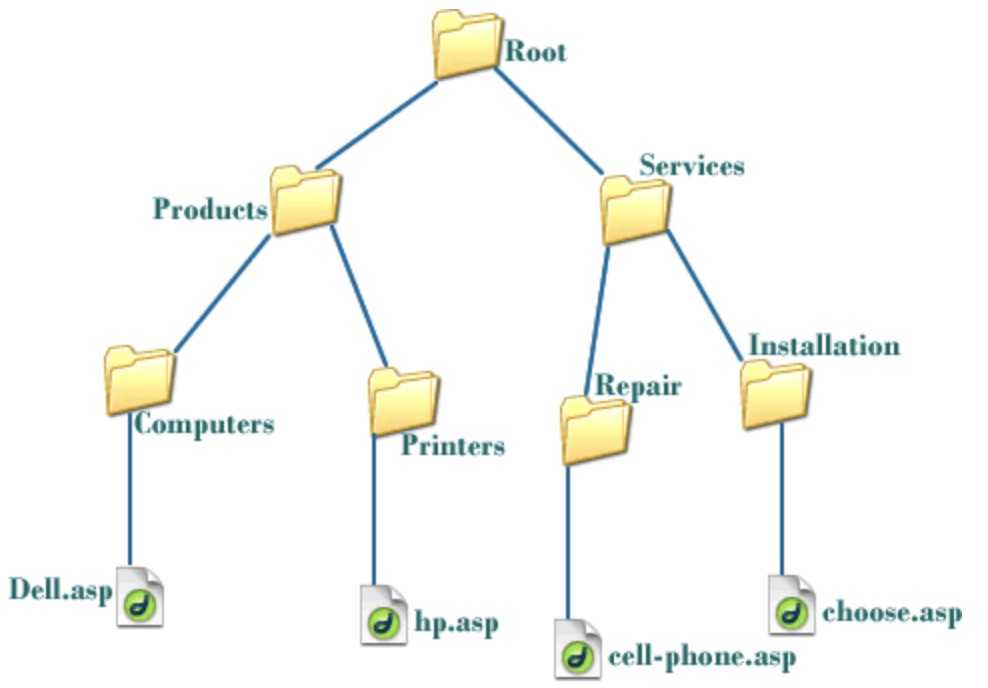
👉 트리는 계층형 구조이다
Node: 트리에서 데이터를 저장하는 기본 요소
Root Node: 트리 맨 위에 있는 노드
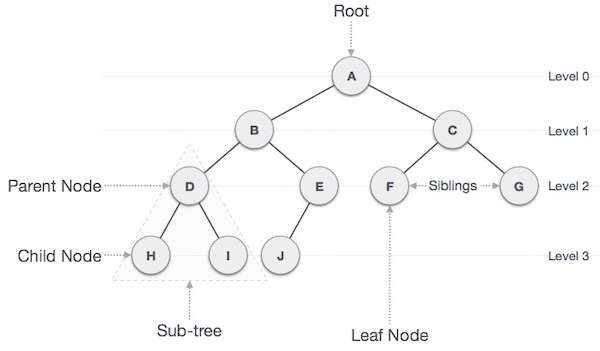
Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
Parent Node: 어떤 노드의 상위 레벨에 연결된 노드
Child Node: 어떤 노드의 하위 레벨에 연결된 노드
Leaf Node(Terminal Node): Child Node가 하나도 없는 노드
Sibling: 동일한 Parent Node를 가진 노드
Depth: 트리에서 Node가 가질 수 있는 최대 Level

트리의 종류
: 이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대힙, 최소힙) 등

  • 이진 트리(Binary Tree) 특징
    : 각 노드가 최대 두 개의 자식을 가진다 
      o      Level 0 
    o o o    Level 1
   o  o  o   Level 2 # 이진 트리(X)

      o      Level 0 
    o   o    Level 1
   o o o     Level 2 # 이진 트리(O)
  • 완전 이진 트리(Complete Binary Tree) 특징
    : 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입해야 한다 
      o      Level 0
    o   o    Level 1
     o o     Level 2  # -> 이진 트리 O 완전 이진 트리 X

      o      Level 0
    o   o    Level 1
   o o o     Level 2  # -> 이진 트리 O 완전 이진 트리 O

완전 이진 트리 표현

👉 트리 구조를 표현하는 방법은 1) 직접 클래스를 구현해서 사용하는 방법 2) 배열로 표현하는 방법이 있다. 트리 구조를 배열에 저장하는 것은 완전 이진 트리를 이용해 가능하다. 완전 이진 트리는 왼쪽부터 데이터가 쌓이는데, 이를 순서대로 배열에 쌓으면서 표현 가능하다

트리를 구현할 때는 편의성을 위해 0번째 인덱스는 사용되지 않는다. 
그래서 None 값을 배열에 넣고 시작한다. [None]

      8      Level 0 -> [None, 8] 첫번째 레벨의 8을 넣고,
    6   3    Level 1 -> [None, 8, 6, 3] 다음 레벨인 6, 3을 넣고
   4 2 5     Level 2 -> [None, 8, 6, 3, 4, 2, 5] 다음 레벨인 4, 2, 5를 넣음

1. 현재 인덱스 * 2 -> 왼쪽 자식의 인덱스
2. 현재 인덱스 * 2 + 1 -> 오른쪽 자식의 인덱스
3. 현재 인덱스 // 2 -> 부모의 인덱스
 
1번째 인덱스인 8의 왼쪽 자식은 6, 오른쪽 자식은 3 
그러면 1 * 2 = 2번째 인덱스 6
그러면 1 * 2 + 1 = 3번째 인덱스 3
부모를 찾아보면, 3 // 2 = 1번째 인덱스 8 

[None, 8, 6, 3, 4, 2, 5] 는
8 밑에 6, 3 이 있고, 6, 3 밑에 4, 2, 5가 있는 완전 이진 트리
  • 완전 이진 트리 높이
    : 트리의 높이(Height)는, 루트 노드부터 가장 아래 리프 노드까지의 길이
      o      Level 0  # 루트 노드
    o   o    Level 1
   o o o     Level 2  # 가장 아래 리프 노드

이 트리의 높이는 2 - 0 = 2

즉, 레벨을 k라고 한다면 각 레벨에 최대로 들어갈 수 있는 노드의 개수는
2k2^k 개수

❓ 만약 높이가 h 인데 모든 노드가 꽉 차 있는 완전 이진 트리라면
모든 노드의 개수는 몇개일까?

이를 수식으료 표현하면

1 + 2^1 + 2^2 + 2^3 + 2^4 ..... 2^h

즉, 높이가 h 일 때 최대 노드의 개수는 2(h+1)−12^(h+1) -1개 입니다.

그러면 이 때 최대 노드의 개수가 N이라면, h 는 뭘까?

2(h+1)−1=N2^(h+1) -1 = N
→ h=log2(N+1)−1h = log_2(N+1)-1

즉, 완전 이진 트리 노드의 개수가 N일 때 최대 높이가 log2(N+1)−1log_2(N+1) - 1 이므로 이진 트리의 높이는 최대로 해봤자 O(log(N))O(log(N))

힙

📖 힙은 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)

💡 항상 최대의 값들이 필요한 연산이 있다면 힙 사용
힙은 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있도록 하는 자료구조. 부모 노드의 값이 자식 노드의 값보다 항상 커야 한다. 가장 큰 값은 모든 자식보다 커야 하기 때문에 가장 위로 가는 방식

      8      Level 0
    6   3    Level 1
     2 1     Level 2  # -> 이진 트리 O 완전 이진 트리 X 이므로 힙이 아닙니다!

      8      Level 0
    6   3    Level 1  # -> 이진 트리 O 완전 이진 트리 O 인데 모든 부모 노드의 값이
   4 2 1     Level 2  # 자식 노드보다 크니까 힙이 맞습니다!


      8      Level 0
    6   3    Level 1  # -> 이진 트리 O 완전 이진 트리 O 인데 모든 부모 노드의 값이
   4 2 5     Level 2  # 자식 노드보다 크지 않아서 힙이 아닙니다..!

💡 힙은 최대값을 맨 위로 올릴 수도 있고, 최솟값을 맨 위로 올릴 수도 있다. 최댓값이 맨 위인 힙을 Max 힙, 최솟값이 맨 위인 힙을 Min 힙이라고 한다

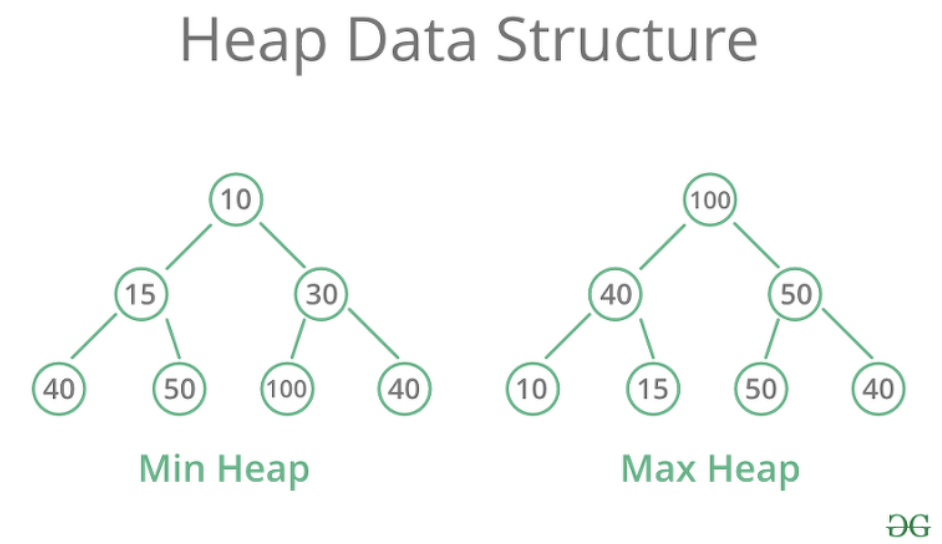
맥스 힙에 원소 추가

👉 힙의 규칙
힙은 항상 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있어야 한다.
따라서, 원소를 추가하거나 삭제할 때도 위의 규칙이 지켜져야 한다.
원소를 추가할 때 다음과 같이 진행한다

  1. 원소를 맨 마지막에 넣는다
  2. 부모 노드와 비교한다. 만약 더 크다면 자리를 바꾼다
  3. 부모 노드보다 작거나 가장 위에 도달하지 않을 때까지 2 과정을 반복한다
 이 맥스 힙에서 9를 추가
      8      Level 0
    6   3    Level 1  
   4 2 1     Level 2 

1. 맨 마지막에 원소를 넣는다

      8      Level 0
    6   3    Level 1  
   4 2 1 9   Level 2 

2-1. 부모 노드와 비교. 3보다 9가 더 크니까 둘의 자리를 변경

      8      Level 0
    6   3    Level 1  
   4 2 1 9   Level 2 

      8      Level 0
    6   9    Level 1  
   4 2 1 3   Level 2 

2-2. 다시 부모 노드와 비교. 8보다 9가 더 크니까 둘의 자리를 변경

      8      Level 0
    6   9    Level 1  
   4 2 1 3   Level 2 

      9      Level 0
    6   8    Level 1  
   4 2 1 3   Level 2 

3. 가장 위에 도달했으므로 멈춘다

      9      Level 0
    6   8    Level 1  
   4 2 1 3   Level 2

예시) 

#맥스 힙에 원소 추가

class MaxHeap:
    def __init__(self):
        self.items = [None]

    def insert(self, value):
        self.items.append(value)
        cur_index = len(self.items)-1

        while cur_index >1: #cur_index가 1이 된다면 정상을 찍은 거라 다른 것가 비교 안 해도 됨
            parent_index = cur_index // 2
            if self.items[parent_index] < self.items[cur_index]:
                self.items[parent_index], self.items[cur_index] = self.items[cur_index], self.items[parent_index]
                cur_index = parent_index
            else:
                break


max_heap = MaxHeap()
max_heap.insert(3)
max_heap.insert(4)
max_heap.insert(2)
max_heap.insert(9)
print(max_heap.items)  # [None, 9, 4, 2, 3] 가 출력되어야 합니다!

✅ 시간 복잡도
완전 이진트리의 최대 높이는 O(log(N))O(log(N))
그러면, 반복하는 최대 횟수도 O(log(N))O(log(N))
맥스 힙의 원소 추가는 O(log(N))O(log(N)) 만큼의 시간 복잡도를 가진다고 분석할 수 있다

맥스 힙에 원소 제거

👉 최대 힙에서 원소를 삭제하는 방법은 최댓값, 루트 노드를 삭제하는 것이다
스택과 같이 맨 위에 원소만 제거할 수 있고, 다른 위치의 노드를 삭제할 수는 없다.

진행 방법
1. 루트 노드와 맨 끝에 원소를 교체한다
2. 맨 뒤에 있는 원소를(원래 루트 노드) 삭제하다
3. 변경된 노드와 자식 노드를 비교한다. 두 자식 중 더 큰 자식과 비교해 자신보다 더 크다면 자리를 바꾼다
4. 자식 노드 둘 보다 부모 노드가 크거나 가장 바닥에 도달하지 않을 때까지 3 과정을 반복한다 

이 맥스 힙에서 원소를 제거 (항상 맨 위의 루트 노드가 제거)
      8      Level 0
    6   7    Level 1  
   2 5 4 3   Level 2 

1. 루트 노드와 맨 끝에 있는 원소를 교체

      8      Level 0
    6   7    Level 1  
   2 5 4 3   Level 2 

      3      Level 0
    7   6    Level 1  
   2 5 4 8   Level 2 

2. 맨 뒤에 있는 원소를 (원래 루트 노드)를 삭제

      3      Level 0
    6   7    Level 1  
   2 5 4 X   Level 2 

3-1. 변경된 노드를 더 큰 자식 노드와 비교해야함 
우선 부모와 왼쪽 자식을 비교 그리고 부모와 오른쪽 자식을 비교
그리고 부모 보다 큰 자식 중, 더 큰 자식과 변경
왼쪽 자식인 6과 오른쪽 자식인 7 중에서 7이 더 크고, 부모인 3보다 크니까 둘의 자리를 변경

      3      Level 0
    6   7    Level 1  
   2 5 4     Level 2 

      7      Level 0
    6   3    Level 1  
   2 5 4     Level 2 

3-2. 다시 자식 노드와 비교 
우선 부모와 왼쪽 자식을 비교
왼쪽 자식인 4는 부모인 3보다 더 크니까 둘의 자리를 변경

      7      Level 0
    6   3    Level 1  
   2 5 4     Level 2 

      7      Level 0
    6   4    Level 1  
   2 5 3     Level 2 


4. 가장 아래 레벨에 도달했으므로 멈춤

      7      Level 0
    6   4    Level 1  
   2 5 3     Level 2 

5. 제거한 원래 루트 노드, 8을 반환

예) 

#맥스 힙의 원소 제거

class MaxHeap:
    def __init__(self):
        self.items = [None]

    def insert(self, value):
        self.items.append(value)
        cur_index = len(self.items) - 1

        while cur_index > 1:  # cur_index 가 1이 되면 정상을 찍은거라 다른 것과 비교 안하셔도 됩니다!
            parent_index = cur_index // 2
            if self.items[parent_index] < self.items[cur_index]:
                self.items[parent_index], self.items[cur_index] = self.items[cur_index], self.items[parent_index]
                cur_index = parent_index
            else:
                break

    def delete(self):
        self.items[1], self.items[-1] = self.items[-1], self.items[1]
        prev_max = self.items.pop()
        cur_index  = 1
        while cur_index <= len(self.items)-1:
            l_child_index = cur_index * 2
            r_child_index = cur_index * 2 + 1
            max_index = cur_index

            if l_child_index <= len(self.items) -1 and self.items[l_child_index] > self.items[max_index]:
                max_index = l_child_index
            if r_child_index <= len(self.items) -1 and self.items[r_child_index] > self.items[max_index]:
                max_index = r_child_index
            if max_index == cur_index:
                break
            self.items[cur_index], self.items[max_index] = self.items[max_index], self.items[cur_index]
            cur_index = max_index
        return prev_max


max_heap = MaxHeap()
max_heap.insert(8)
max_heap.insert(6)
max_heap.insert(7)
max_heap.insert(2)
max_heap.insert(5)
max_heap.insert(4)
print(max_heap.items)  # [None, 8, 6, 7, 2, 5, 4]
print(max_heap.delete())  # 8 을 반환해야 합니다!
print(max_heap.items)  # [None, 7, 6, 4, 2, 5]

그래프

  • 연결 관계

👉 그래프에서 사용되는 용어들
노드(Node): 연결 관계를 가진 각 데이터를 의미합니다. 정점(Vertex)이라고도 합니다.
간선(Edge): 노드 간의 관계를 표시한 선.
인접 노드(Adjacent Node): 간선으로 직접 연결된 노드(또는 정점)

🧐 그래프 종류

  • 유방향 그래프(Directed Graph): 방향이 있는 간선을 가진다. 간선은 단방향 관계를 나타내며, 각 간선은 한 방향으로만 진행할 수 있다
  • 무방향 그래프(Undirected Graph): 방향이 없는 간선을 가진다

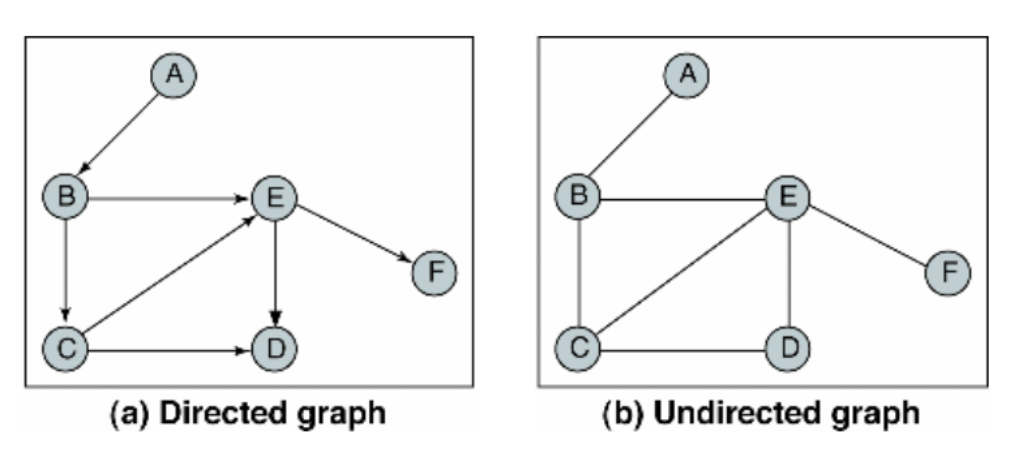
👉 그래프 개념을 컴퓨터에서 표현하는 방법
1) 인접 행렬(Adjacency Matrix): 2차원 배열로 그래프의 연결 관계를 표현
2) 인접 리스트(Adjacnecy List): 링크드 리스트로 그래프의 연결 관계를 표현

          2 - 3
          ⎜       
      0 - 1

1. 이를 인접 행렬, 2차원 배열로 나타내면 다음과 같습니다!
  0  1  2  3
0 X  O  X  X
1 O  X  O  X
2 X  O  X  O
3 X  X  O  X

이걸 배열로 표현하면 다음과 같습니다!
graph = [
    [False, True, False, False],
    [True, False, True, False],
    [False, True, False, True],
    [False, False, True, False]
]

2. 이번에는 인접 리스트로 표현해보겠습니다!
인접 리스트는 모든 노드에 연결된 노드에 대한 정보를 차례대로 다음과 같이 저장합니다.

0 -> 1
1 -> 0 -> 2
2 -> 1 -> 3
3 -> 2

이를 딕셔너리로 표현하면 다음과 같습니다!
graph = {
    0: [1],
    1: [0, 2]
    2: [1, 3]
    3: [2]
}

👉 인접 행렬로 표현하면 즉각적으로 0과 1이 연결되었는지 여부를 바로 알 수 있다. 그러나 모든 조합의 연결 여부를 저장해야 하기 때문에 O(노드2)O(노드^2) 만큼의 공간을 사용해야 한다
👉 인접 리스트로 표현하면 즉각적으로 연결되었는지 알 수 없고, 각 리스트를 돌아봐야 한다. 따라서 연결되었는지 여부를 알기 위해서 최대 O(간선)O(간선) 만큼의 시간을 사용해야 한다

DFS

📖 자료의 검색, 트리나 그래프를 탐색하는 방법. 한 노드를 시작으로 인접한 다른 노드를 재귀적으로 탐색해가고 끝까지 탐색하면 다시 위로 와서 다음을 탐색하여 검색한다

DFS 와 BFS 는 그 탐색하는 순서에서 차이가 있다
DFS 는 끝까지 파고드는 것이고, BFS 는 갈라진 모든 경우의 수를 탐색해보고 오는 것

👉 DFS는 끝까지 파고드는 것이라, 그래프의 치대 깊이 만큼 공간을 요구한다. 따라서 공간을 적게 쓴다. 그러나 최단 경로를 탐색하기 쉽지 않다

👉 BFS는 모든 분기되는 수를 다 보고 올 수 있기 때문에 최단 경로를 쉽게 찾을 수 있다. 그러나, 모든 분기되는 수를 다 저장하다보니 공간을 많이 써야하고, 모든 걸 다 보고 오다보니 시간이 더 오래 걸릴 수 있다

DFS 구현

DFS 는 탐색하는 원소를 최대한 깊게 따라가야 한다
이걸 다시 말하면 인접한 노드 중 방문하지 않은 모든 노드들을 저장해두고,
가장 마지막에 넣은 노드들만 꺼내서 탐색하면 된다. (스택 이용)

  1. 루트 노드부터 시작한다
  2. 현재 방문한 노드를 visited 에 추가한다
  3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드에 방문한다
  4. 2부터 반복한다
# 인접 리스트 방식
graph = {
    1: [2, 5, 9],
    2: [1, 3],
    3: [2, 4],
    4: [3],
    5: [1, 6, 8],
    6: [5, 7],
    7: [6],
    8: [5],
    9: [1, 10],
    10: [9]
}
visited = []


def dfs_recursion(adjacent_graph, cur_node, visited_array):
    visited_array.append(cur_node)
    for adjacent_node in adjacent_graph[cur_node]:
        if adjacent_node not in visited_array:
            dfs_recursion(adjacent_graph, adjacent_node, visited_array)
    return


dfs_recursion(graph, 1, visited)  # 1 이 시작노드
print(visited)  # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 이 출력되어야 함

🔥 재귀 함수를 통해서는 무한정 깊어지는 노드가 있는 경우 에러가 발생할 수 있다.
이를 피하기 위새 스택을 이용해 DFS를 구현할 수 있다

  1. 루트 노드를 스택에 넣는다
  2. 현재 스택의 노드를 빼서 visited 에 추가한다
  3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 스택에 추가한다
  4. 2부터 반복한다
  5. 스택이 비면 탐색을 종료한다
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
    1: [2, 5, 9],
    2: [1, 3],
    3: [2, 4],
    4: [3],
    5: [1, 6, 8],
    6: [5, 7],
    7: [6],
    8: [5],
    9: [1, 10],
    10: [9]
}


def dfs_stack(adjacent_graph, start_node):
    stack = [start_node]
    visited = []
    while stack:
        curent_node = stack.pop()
        visited.append(curent_node)
        for adjacent_node in adjacent_graph[curent_node]:
            if adjacent_node not in visited:
                stack.append(adjacent_node)
    return visited


print(dfs_stack(graph, 1))  
# [1, 9, 10, 5, 8, 6, 7, 2, 3, 4]

BFS

📖 한 노드를 시작으로 인접한 모든 정점들을 우선 방문하는 방법. 더 이상 방문하지 않은 정점이 없을 때까지 방문하지 않은 모든 정점들에 대해서도 넓이 우선 검색을 적용한다

BFS 구현

BFS는 현재 인접한 노드 먼저 방문해야하다
이걸 다시 말하면 인접한 노드 중 방문하지 않은 모든 노드들을 저장해두고,
가장 처음에 넣은 노드를 꺼내서 탐색하면 된다 (큐 이용)

  1. 루트 노드를 큐에 넣는다
  2. 현재 큐의 노드를 빼서 visited 에 추가한다
  3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 큐에 추가한다
  4. 2부터 반복한다
  5. 큐가딕 비면 탐색을 종료한다
def bfs_queue(adj_graph, start_node):
    queue = [start_node]
    visited = []

    while queue:
        current_node = queue.pop(0)
        visited.append(current_node)
        for adjacent_node in adj_graph[current_node]:
            if adjacent_node not in visited:
                queue.append(adjacent_node)

    return visited

print(bfs_queue(graph, 1))

Dynamic Programming

피보나치 수열

👉 즉, n번째 피보나치 수를 Fibo(n)라고 표현한다면,
Fibo(1) 은 1이고,
Fibo(2) 도 1

Fibo(3) 부터는 이전 값과 이전 이전 값의 합
즉, Fibo(3) = Fibo(1) + Fibo(2) = 1 + 1 = 2 

Fibo(4) = Fibo(3) + Fibo(2) = 2 + 1 = 3
Fibo(5) = Fibo(4) + Fibo(3) = 3 + 2 = 5
Fibo(6) = Fibo(5) + Fibo(4) = 5 + 3 = 8 .....
Fibo(n) = Fibo(n - 1) + Fibo(n-2) 
input = 20


def fibo_recursion(n):
    if n == 1 or n == 2:
        return 1
    return fibo_recursion(n - 1) + fibo_recursion(n - 2)


print(fibo_recursion(input))  # 6765

👉 계산해야 하는 수가 많아지면 계산 시간이 매우 오래 걸린다

동적 계획법 (Dynamic Programming)

: 복잡한 문제를 간단히 여러 개의 문제로 나누어 푸는 방법

  • 결과를 기록하는 것 메모이제이션(Memoization)
  • 문제를 쪼갤 수 있는 구조 겹치는 부분 문제(Overlapping Subproblem)

동적 계획법 활용해 피보나치 수열 문제 풀기

  1. 메모용 데이터를 만든다. 처음 값인 Fibo(1), Fibo(2) 는 각각 1씩 넣어서 저장해둔다
  2. Fibo(n) 을 구할 때 만약 메모에 그 값이 있다면 바로 반환한다
  3. Fibo(n) 을 처음 구했다면 메모에 그 값을 기록한다
input = 50

# memo 라는 변수에 Fibo(1)과 Fibo(2) 값을 저장해놨습니다!
memo = {
    1: 1,
    2: 1
}


def fibo_dynamic_programming(n, fibo_memo):
    if n in fibo_memo:
        return fibo_memo[n]
    nth_fibo = fibo_dynamic_programming(n-1, fibo_memo) + fibo_dynamic_programming(n-2, fibo_memo)
    fibo_memo[n] = nth_fibo
    return nth_fibo


print(fibo_dynamic_programming(input, memo))
profile
원
이전 포스트

파이썬 자료구조 3

다음 포스트

Django 1

0개의 댓글