머신러닝 기초2

논리 회귀(Logistic regression)

🔰 논리 회귀: 입력값과 범주 사이의 관계를 구하는 것
선형 회귀로 풀 수 없는 문제가 등장함에 따라 문제를 해결하기 위해 특정 변수에 대한 확률값을 선형이 아닌 S커브 형태를 적용한 것. S커브를 함수로 표현해낸 것이 로지스틱 함수(logistic function).
딥러닝에서는 시그모이드 함수(Sigmoid function)이라고 한다

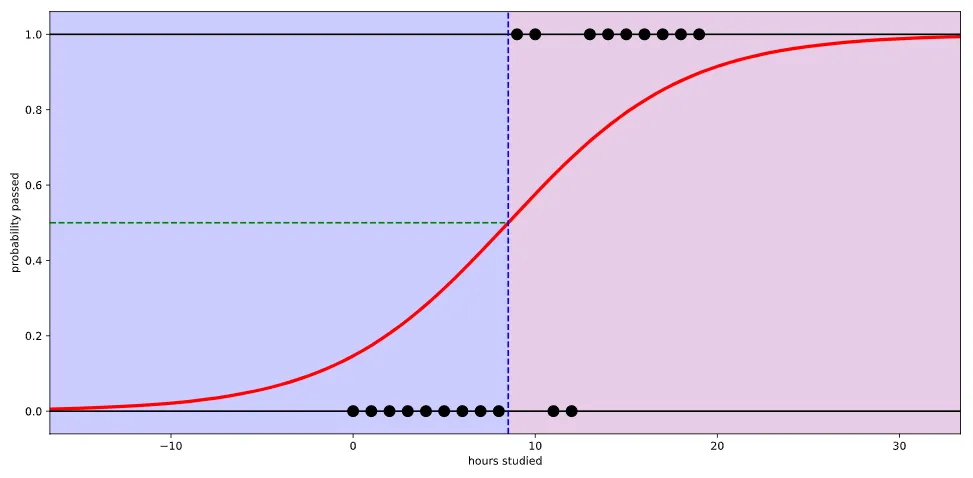
로지스틱 함수는 입력값(x)으로 어떤 값이든 받을 수가 있지만 출력 결과(y)는 항상 0에서 1사이 값이 된다

실질적인 계산은 선형 회귀와 똑같지만 출력에 시그모이드 함수를 붙여 0에서 1사이의 값을 가지도록 한다

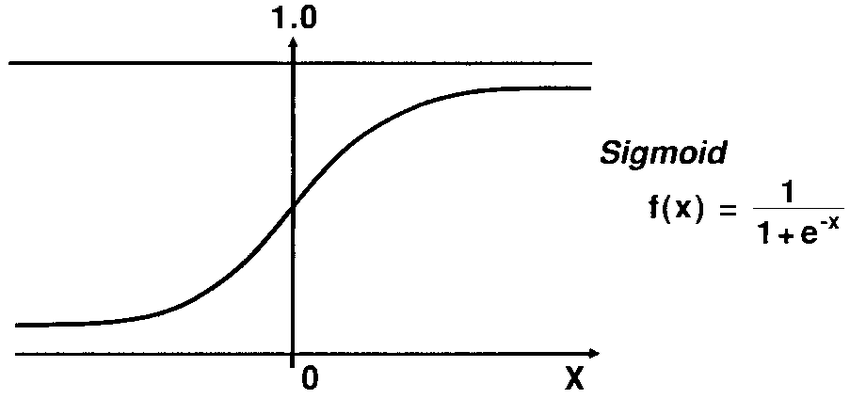
시그모이드 함수
x(입력)가 음수 방향으로 갈 수록 y(출력)가 0에 가까워지고
x(입력)가 양수 방향으로 갈 수록 y(출력)가 1에 가까워진다
즉, 시그모이드 함수를 통과하면 0 에서 1 사이 값이 나온다

선형 회귀에서의 가설 $H(x) = Wx + b$
논리 회귀에서의 가설 $H(x) = \frac{1}{1 + e^{-(Wx + b)}}b$

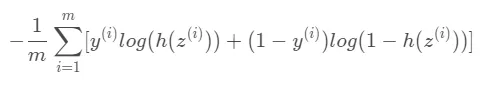
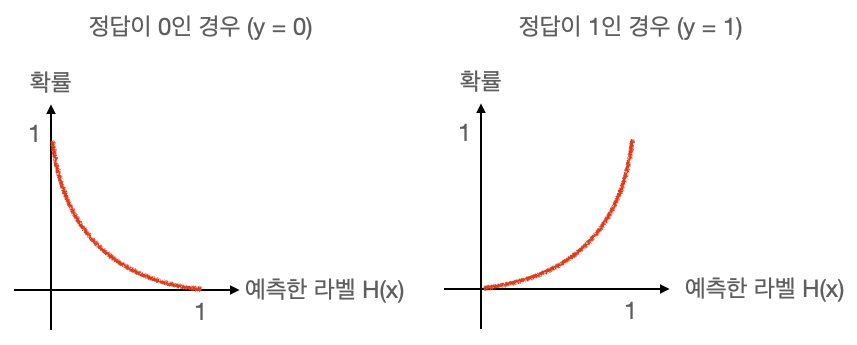
예측한 라벨이 0일 경우 확률이 1(=100%)이 되도록 해야하고, 예측한 라벨이 1일 경우 확률이 0(=0%)이 되도록 만들어야 한다. 반대로 정답 라벨 y가 1일 경우에는, 예측한 라벨 1일 때 확률이 1(=100%)이 되도록 만들어야 한다.

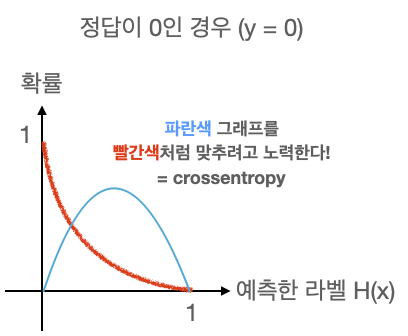
crossentropy는 파란색 그래프를 빨간색 그래프처럼 만들어주기 위해 노력하는 함수.
(선형 회귀를 했을때 정답값을 나타내는 점과 우리가 세운 가설 직선의 거리를 최소화하려고 했던 거리 함수처럼)

다항 논리 회귀 (Multinomial logistic regression)

☑️원핫 인코딩은 다항 분류 (Multi-label classification) 문제를 풀 때 출력값의 형태를 가장 예쁘게 표현할 수 있는 방법. 다항 논리 회귀도 다항 분류에 속하기 때문에 원핫 인코딩 방법을 사용한다.

원핫 인코딩을 만드는 방법은 아래와 같다
1. 클래스(라벨)의 개수만큼 배열을 0으로 채운다
2. 각 클래스의 인덱스 위치를 정한다
3. 각 클래스에 해당하는 인덱스에 1을 넣는다

Softmax 함수와 손실함수

Softmax는 선형 모델에서 나온 결과(Logit)를 모두가 더하면 1이 되도록 만들어주는 함수. 다 더하면 1이 되도록 만드는 이유는 예측의 결과를 확률(=Confidence)로 표현하기 위함. One-hot encoding을 할때에도 라벨의 값을 전부 더하면 1(100%)이 된다.

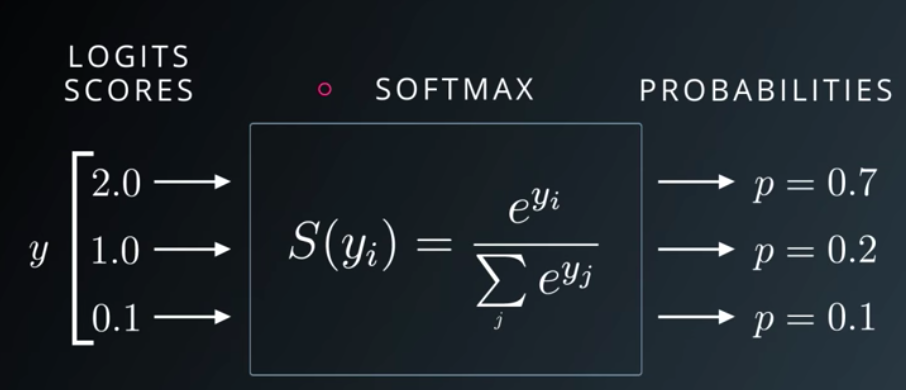
확률 분포의 차이를 계산할 때는 Crossentropy 함수를 쓴다. 항이 여러개가 되었을 뿐 차이는 이진 논리 회귀와 차이는 없다. 데이터셋의 정답 라벨과 우리가 예측한 라벨의 확률 분포 그래프를 구해서 Crossentropy로 두 확률 분포의 차이를 구한 다음 그 차이를 최소화하는 방향으로 학습 시킨다.

머신러닝 모델

Support vector machine(SVM)

강아지와 고양이를 구분하는 문제를 푼다고 가정해 보자면,
구분하는 문제를 푸는 것은 분류 문제(Classification problem)이고 분류 문제를 푸는 모델을 분류기(Classifier)라고 부를 수 있다.

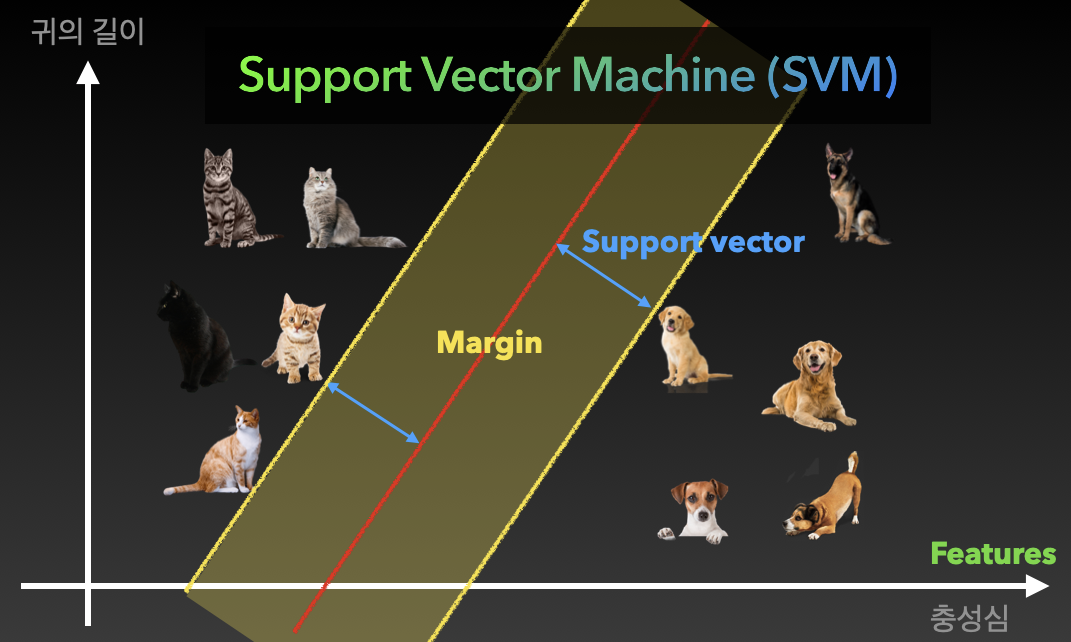
각 그래프의 축을 Feature(특징)라고 부르고 각 고양이, 강아지와 우리가 그린 빨간 벡터를 Support vector라고 부른다. 그리고 그 벡터의 거리를 Margin이라고 한다.
Margin이 넓어지도록 이 모델을 학습시켜 훌륭한 Support vector machine을 만들 수 있다.
🔻예외 상황 발생
만약 충성심이 강한 개냥이가 등장한다면? Feature(특성)의 개수를 늘려서 학습시킨다. 현재는 귀의 길이, 충성심 2개의 특성만 있지만 새로운 특성을 추가시켜 3차원 그래프를 그려 구분할 수 있다

KNN(k-Nearest neighbors)

KNN은 비슷한 특성을 가진 개체끼리 군집화하는 알고리즘. 예를 들어 하얀 고양이가 새로 나타났을 때 일정 거리안에 다른 개체들의 개수(k)를 보고 자신의 위치를 결정하게하는 알고리즘

Decision tree(의사결정 나무)

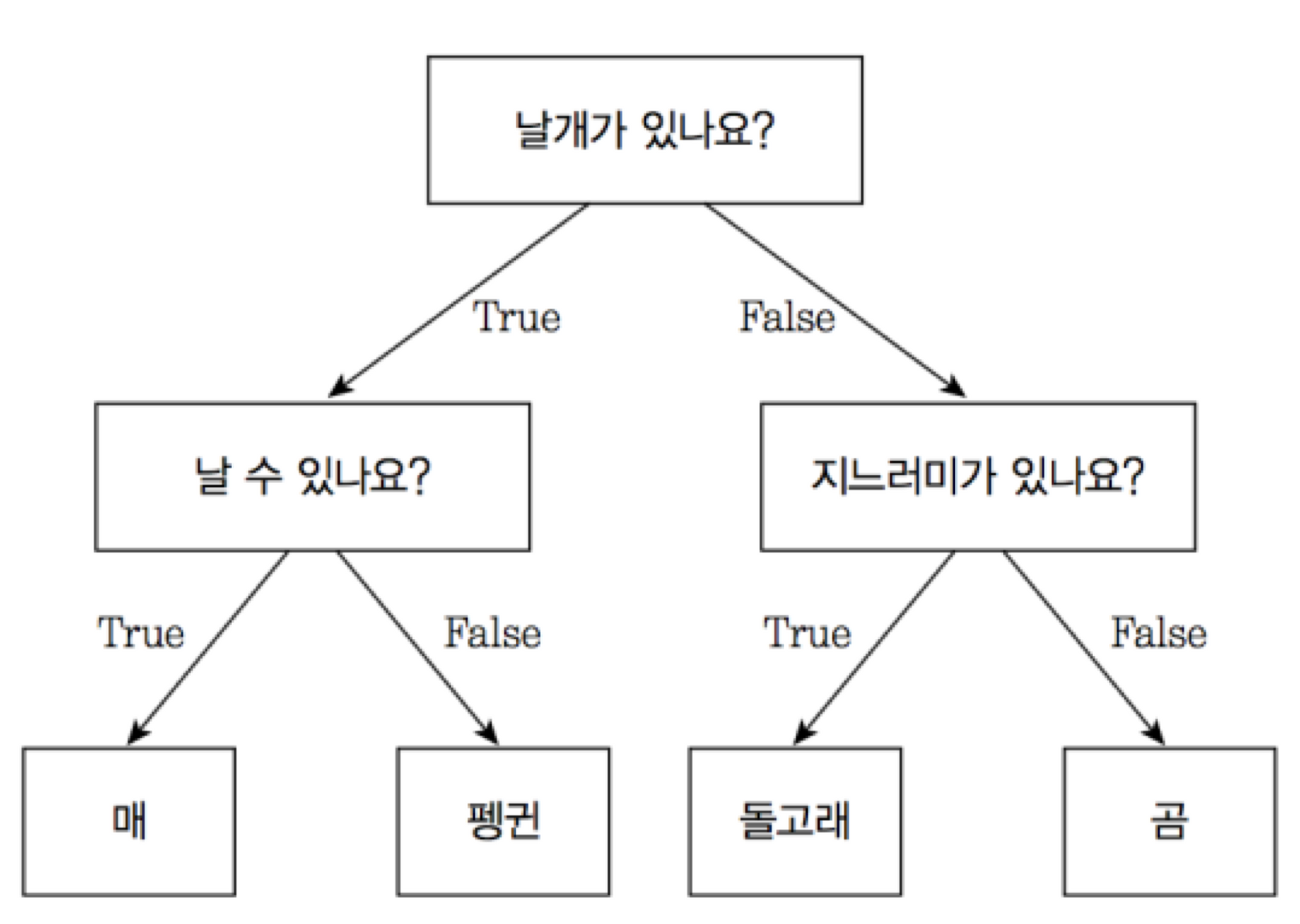
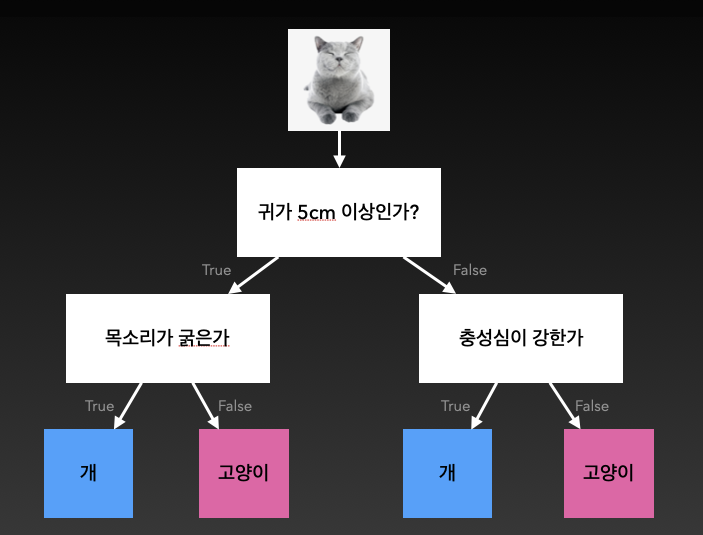
Random forest

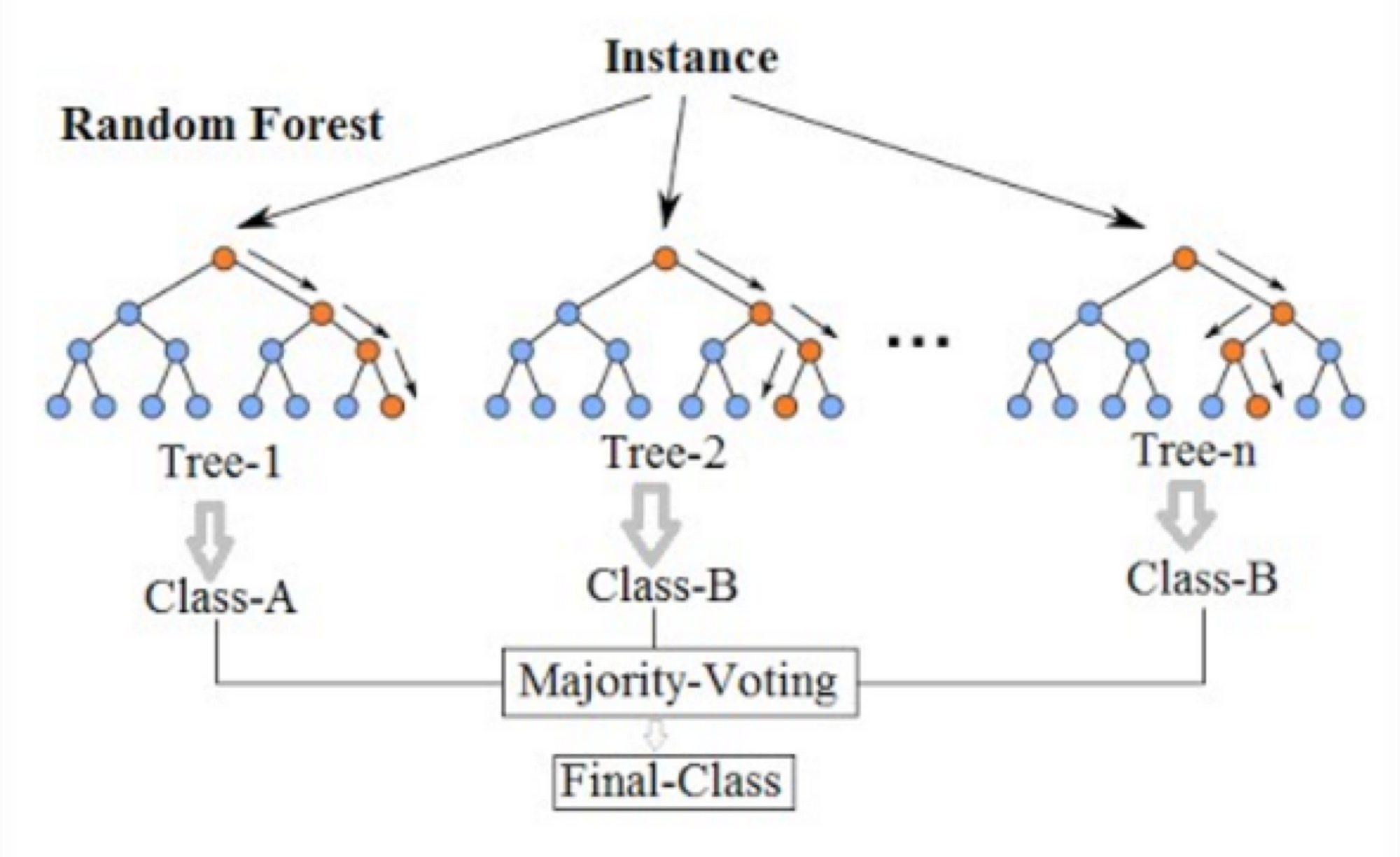
의사결정나무를 여러개 합친 모델. 의사결정나무는 한 사람이 결정하는 것이라고 하면 랜덤 포레스트는 자유민주주의라고 보면 된다. 각각의 의사결정나무들이 결정을 하고 마지막에 투표(Majority voting)을 통해 최종 답을 결정하게 된다

머신러닝 전처리

전처리(Preprocessing)

전처리는 넓은 범위의 데이터 정제 작업을 뜻한다
필요없는 데이터를 지우고 필요한 데이터만을 취하는 것, null 값이 있는 행을 삭제하는 것, 정규화(Normalization), 표준화(Standardization) 등의 많은 작업들을 포함한다

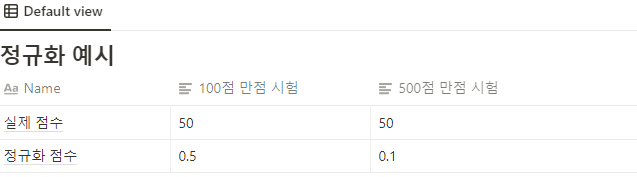
정규화(Normalization)

정규화는 데이터를 0과 1사이의 범위를 가지도록 만든다.
같은 특성의 데이터 중에서 가장 작은 값을 0으로 만들고, 가장 큰 값을 1로 만든다
$X' = \frac{X - X_{최소}}{X_{최대} - X_{최소}}$

표준화 (Standardization)

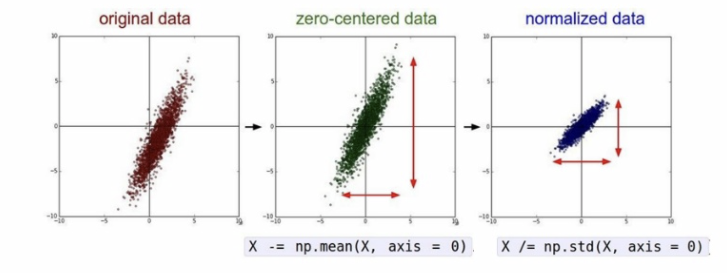
표준화는 데이터의 분포를 정규분포로 바꿔준다.
즉 데이터의 평균이 0이 되도록하고 표준편차가 1이 되도록 만들어준다
$X' = \frac{X - X_{평균}}{X_{표준편차}}$
데이터의 평균을 0으로 만들어주면 데이터의 중심이 0에 맞춰지게(Zero-centered) 된다.
그리고 표준편차를 1로 만들어 주면 데이터가 정규화(Normalized) 된다.
이렇게 표준화를 시키게 되면 일반적으로 학습 속도(최저점 수렴 속도)가 빠르고, Local minima에 빠질 가능성이 적다