머신러닝 기초

머신러닝

• 인공지능 안에 머신러닝이 속하고, 머신러닝 안에 딥러닝이 속한다

머신러닝의 회귀와 분류

• 회귀 (Regression): 출력값이 연속적인 소수점으로 예측하게 하도록 푸는 방법. 입력값과 출력값이 결정된다
• 분류 (Classification): 대학교 시험 전 날 공부한 시간을 가지고 해당 과목의 이수여부(Pass or fail)를 예측하는 문제. 0이면 미이수(Fail), 1이면 이수(Pass) -> 이진 분류(Binary classification)

Q) 대학교 시험 전 날 공부한 시간을 가지고 해당 과목의 성적(A, B, C, D, F)을 예측하는 문제
: 클래스를 5개의 클래스로 나눔 -> 다중 분류(Multi-class classification, Multi-label classification)

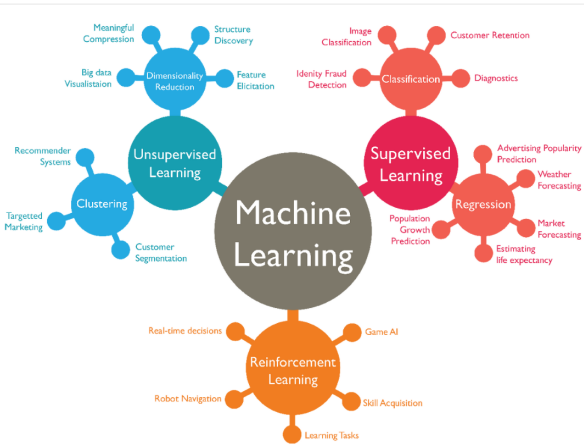
기계학습 방법: 지도학습, 비지도 학습, 강화학습

1) 지도 학습(Supervised learning): 정답을 알려주면서 학습시키는 방법
-> 입력값에 정답을 하나씩 입력해주는 작업을 하게 되는 경우가 있는데 그 과정을 노가다
라벨링(Labeling, 레이블링) 또는 어노테이션(Annotation)이라고 한다
2) 비지도 학습 (Unsupervised learning): 정답을 알려주지 않고 군집화(Clustering) 하는 방법
-> 라벨(Label 또는 Class)이 없는 데이터를 가지고 문제를 풀어야 할 때 큰 힘을 발휘
종류) 군집, 시각화와 차원 축소, 연관 규칙 학습
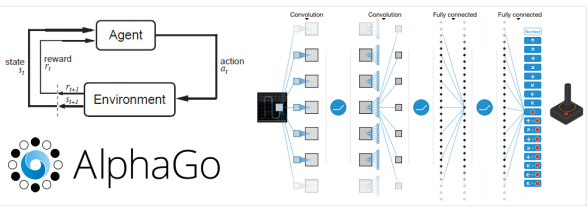
3) 강화 학습(Reinforcement learning): 주어진 데이터없이 실행과 오류를 반복하면서 학습하는 방법 (알파고를 탄생시킨 머신러닝 방법. 행동 심리학에서 나온 이론으로 분류할 수 있는 데이터가 존재하지 않거나, 데이터가 있어도 정답이 따로 정해져 있지 않고, 자신이 한 행동에 대해 보상(Reward)를 받으며
학습하는 것을 의미

선형회귀

(직선= 1차 함수)
$H(x) = Wx + b$
정확한 값을 예측하기 위해서는 임의의 직선(가설)과 점(정답)의 거리가 가까워져야 한다. (=mean squared error)
$Cost = {{1\over N}\sum_{i=1}^{N}{(H(x_i) - y_i) ^ 2}}$
여기서 H(x)는 우리가 가정한 직선이고 y 는 정답 포인트라고 했을 때 H(x)와 y의 거리(또는 차의 절대값)가 최소가 되어야 이 모델이 잘 학습되었다고 말할 수 있다. 임의로 만든 직선 H(x)를 가설(Hypothesis)이라고 하고 Cost를 손실 함수(Cost or Loss function)라고 한다.
-> 점들이 정답값이 되고 선형회귀로 예측한 값이 점선이 되는데 점선과 점이 가까워지도록 학습을 해야한다. Cost function이 작게 나올 수록 정확히 예측했다고 할 수 있다
-> 기게는 w와 b를 계속 바꿔가면서 cost 미니마이즈(최소화되는 방향으로) 학습시킨다

다중 선형 회귀(Multi-variable linear regression)

선형 회귀와 똑같지만 입력 변수가 여러개인 것 (입력값이 2개 이상)
가설 $H(x_1, x_2, ..., x_n) = w_1x_1 + w_2x_2 + ... + w_nx_n + b$인 손실 함수

경사 하강법 (Gradient descent method)

아래는 손실 함수 이미지 예시

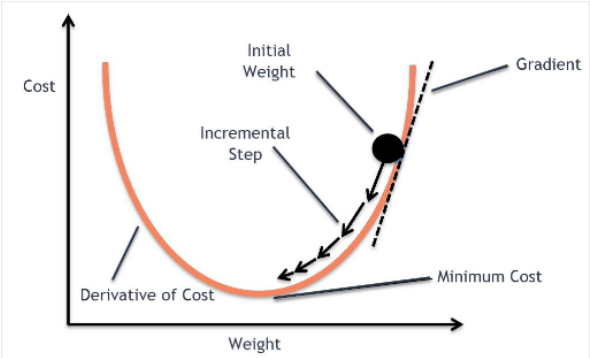
목표는 손실 함수를 최소화(Optimize)하는 것. 손실 함수를 최소화하는 방법은 이 그래프를 따라 점점 아래로 내려가야한다. 컴퓨터는 사람처럼 수식을 풀 수 없기때문에 경사 하강법이라는 방법을 써서 점진적으로 문제를 풀어간다. 처음에 랜덤으로 한 점으로부터 시작하고 좌우로 조금씩 한번씩 움직이면서 이전 값보다 작아지는지를 관찰한다. 한칸씩 전진하는 단위를 Learning rate라고 부르고 그래프의 최소점에 도달하게 되면 학습을 종료한다.

WX + B / cost가 떨어지면 올바른 방향으로 가고 있는 것이고
코스트가 안 떨어지고 반대방향 (위로 간다면) cost가 증가되는 것 (안 좋음)

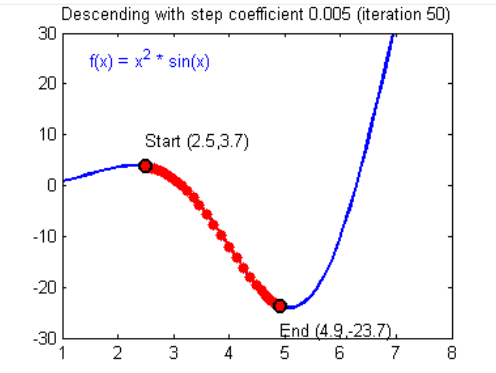
한 칸 한 칸에 전진하는 단위 learning rate (점 사이의 거리)
-> 러닝 레이트가 크면 한번에 많은 점을 움직일 수 있다
-> 러닝 레이트가 작으면 촤소점에 도달하는데 굉장히 오랜 시간이 걸린다
-> 러닝 레이트가 크고 작냐에 따라 학습 시간이 오래 걸리냐 학습 시간이 적게 걸리내
결정된다.

만약 Learning rate가 지나치게 크다면 찾으려는 최소값을 지나치고 검은 점은 계속 진동하다가 최악의 경우에는 발산하게 된다. 이런 상황을 Overshooting이라고 부른다

손실 함수 이미지는 실제로 몇 백 차원이기 때문에 그릴 수도 상상하기도 어렵다
아래는 최대 2차원으로 가정하고 그린 이미지 예시

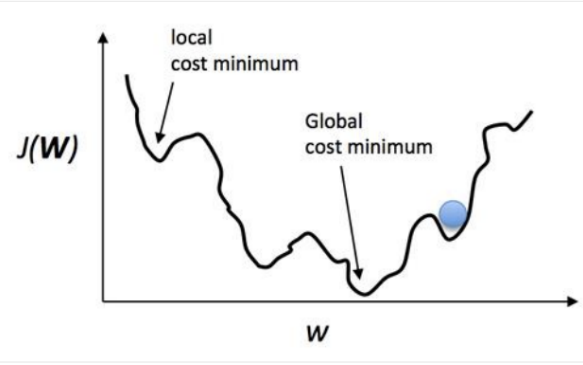
목표는 이 손실 함수의 최소점인 Global cost minimum을 찾는 것. 그런데 한 칸씩 움직이는 스텝(Learning rate)를 잘못 설정할 경우 Local cost minimum에 빠질 가능성이 높다. Cost가 높다는 얘기는 만든 모델의 정확도가 낮다는 말. 따라서 최대한 Global minimum을 찾기 위해 좋은 가설과 좋은 손실 함수를 만들어서 기계가 잘 학습할 수 있도록 만들어야한다

데이터셋

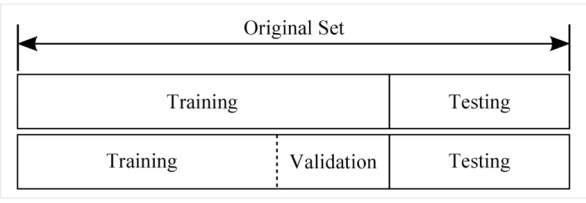
1. Training set (학습 데이터셋, 트레이닝셋) = 교과서
   머신러닝 모델을 학습시키는 용도로 사용합니다. 전체 데이터셋의 약 80% 정도를
   차지

2. Validation set (검증 데이터셋, 밸리데이션셋) = 모의고사
   머신러닝 모델의 성능을 검증하고 튜닝하는 지표의 용도로 사용. 이 데이터는 정답 라벨이 있고, 학습 단계에서 사용하기는 하지만, 모델에게 데이터를 직접 보여주지는 않으므로 모델의 성능에 영향을 미치지는 않는다. 손실 함수, Optimizer 등을 바꾸면서 모델을 검증하는 용도로 사용
   전체 데이터셋의 약 20% 정도 차지

3. Test set (평가 데이터셋, 테스트셋) = 수능
   정답 라벨이 없는 실제 환경에서의 평가 데이터셋. 보통 트레이닝셋은 전체 데이터셋의 80% 정도로 나눠서 사용. 테스트셋은 진짜 모델 검증 때도 쓰지 않은 순수한 데이터셋을 사용

Keras 실습
-sequential: 모델을 정의할 때 쓰는 클래스
-dense:위에서 썼던 가설을 구현할 때 사용
-선형회귀에서는 dense(1)
-hypothesis 가설의 정답값을 이렇게 맞춘다 - fit
-반복학습하는 횟수 epochs