Complexity Analysis

• 복잡도 분석? 알고리즘이 문제를 푸는데 있어서 시간과 공간을 얼마나 차지하는지 나타내는 지표
• 왜 중요한가? Shows how efficient it is.

만약 시간과 공간이 무한정하다면, 모든 경우의 수를 계산하면...알파고도 가능.

Time Complexity

• 가장 큰 숫자와 작은 숫자의 차이를 찾을 때
  • 모든 가능성 시도, n^2
  • 가장 큰수와 작은수를 찾아 시도, 2n
  • Sort를 이용. n = 3. 첫번째꺼, 마지막꺼, 그리고 Subtraction. Constant * 시간복잡도
• Big-O Notation
  • gives an approximation of time complexity
  • Uses general complexity types.

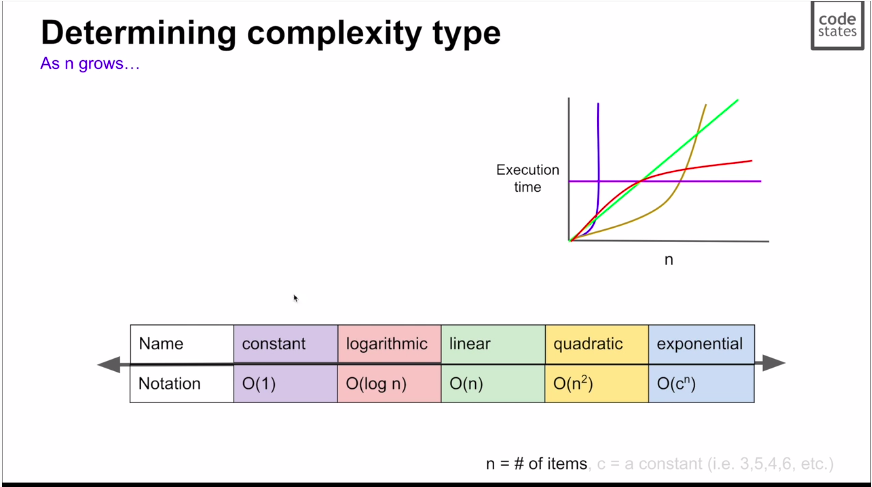
Constant

• O(1): constant, (array lookup, hash table insertion)
• O(log n): logarithmic, Binary Search. 시간복잡도 더 늘어난다 점점 at a decreasing rate
• O(n): linear, linked list. 꾸준하게 늘어난다.
• O(n^2): quadratic, 시간복잡도가 빠르게 는다.
• O(c^n): Exponential, 최악. Recursion, Fibonacci

Data Structure with Time Complexity

• Arrays, Linked Lists, and Trees
• See how time complexity works in these

Stack

• Stack의 대부분 Method들은 마지막에 들어갔다가 나오는 요소만 보기 때문에 O(1)이다. 하지만 탐색을 하거나 무엇의 값에 접근해야 할때는 모든 요소를 뒤져야 해서 O(n)이다.

Queue

• 큐도 스택과 마찬가지로 뒤에 들어가서 앞에 나오는 FIFO 형식이기 때문에 Insert와 Delete같은 Method는 O(1)의 시간복잡도를 가지고 있다. 하지만 탐색 및 접근은 모든 요소를 뒤져야 해 O(n)이다.

Array

• 이어져있는 데이터 타입. 값을 저장할 수 있음.
• Primitive. 이걸가지고 많이 만들 수 있음.
• 연속되는 메모리 블락에 저장되어 있다. This affects efficiency.
• What is the time complexity for looking up the value in a given position?
  • O(1). 룩업과 할당은 이미 index를 알면 바로 실행할 수 있다.
  • 하지만 Insert는 운이 안좋으면 데이타 길이만큼 실행해야 해서 O(n).
  • Remove도 하나를 없애도 나머지도 다 순서를 옮겨야 해서 O(n).
  • Find(value) 도 모든 element를 뒤지면서 찾아야 해 O(n).

Linked List는 Array와 비슷하지만 non-contiguous하기 때문에 Head는 꼭 알아야 한다.

Singly Linked List

• Lookup, Find, Assign: 최악의 경우, 모든 데이터를 봐야 한다. O(n)

• Insert: O(1). 주소만 Pointer에 Reference해주면 된다.
• Remove: 전 순서의 pointer돌려주고 삭제하면 되는데, 전이 뭔지를 몰라서 head로 부터 거슬러 올라가야한다.
  그래서 head삭제는 O(1), 중간은 O(n).

Doubly-Linked Lists

• 나머지는 같고, Remove도 주소를 알고 있기 때문에 O(1)로 바뀐다.

Array: 특정 위치를 찾는 것은 constant, 추가 및 삭제는 linear

Singly-Linked List: 추가는 constant, 탐색과 삭제는 linear

Doubly-Linked Lists: Constant 한 추가와 삭제지만, 노드들이 메모리를 더 잡아 먹는다. Previous에 관한 정보도 담아야해서..

Tree

• 내 값과 Children이라는 Reference를 가지고 있음. Parents 와 Children을 가지고 있다. e) HTML DOM
• Find(): 깊이 우선이던, 넓이 우선이던 모두를 다 탐색해야 한다. 그러므로 O(n). 일반 트리.
  • Binary Search Tree인 경우: Left는 더 작고, Right는 더 크기 때문에 O(log n). 갈수록 시간복잡도가 줄어든다.
  • 하지만 특수한 경우, 한쪽만으로 치우친다면 Linked List와 구조가 같아서 Time Complexity가 O(n)이 된다. Binary Search Tree는 Rebalance를 할 수 있다. Depth의 차이가 1이상 나면 비틀어서 Rebalance한다. 만약 추가할 때 마다 Balance를 비틀어준다면 한쪽으로 치우쳐도 O(log n)이 될 수 있다.
• Binary Search
  • 정렬된 배열과 BST가 있을 때 BST를 사용하고 싶을 경우?
    • 배열은 메모리에서 연속적인 블락을 차지하지만 BST는 구성할 때 Linked List를 쓰기도 하기 때문에 연속적인 메모리를 사용하지 않고 메모리 구석구석에서 연결리스트를 쓴다. 조금더 효율적이다.

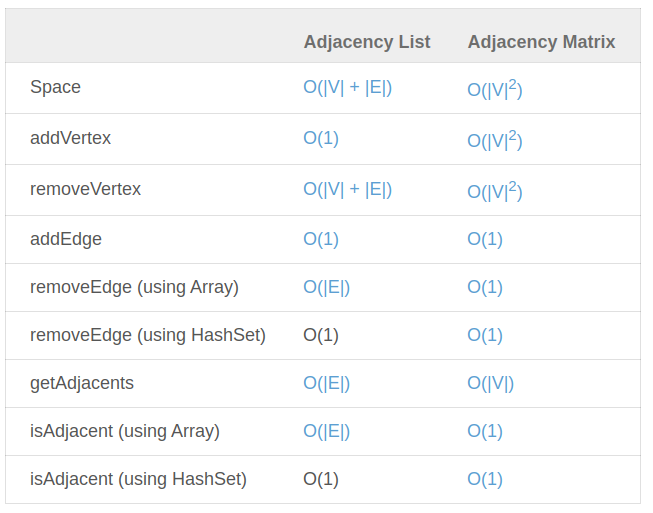
Graph

그래프는 구현하는 방법에 따라 조금씩 미세하게 자이가 난다.

• 인접행렬
  • 인접행렬은 그래프의 연결 관계를 이차원 배열로 나타내는 방식으로, adj[i][j] ,식으로 써 노드 i에서 노드 j로 가는 edge가 있으면 1, 아니면 0으로 정리하면 된다.
    
  • 방향이 없는 무향 그래프라면 방향이 없이 선만 있으면 두 노드가 연결되어 있다는 의미 이기 때문에 인접행렬이 대각 성분을 기준으로 대칭인 성질을 가진다. 위 표의 0을 기준으로 1이 대칭이 된다는 말이다.
    
  • 인접 행렬의 장점은 구현이 쉽다는 점이다. 단점은 모든 노드를 확인 해야 하기 때문에 한 노드에 연결된 모든 노드를 찾아보고 싶은 경우 시간 복잡도가 늘어난다.
• 인접리스트
  • 인접 리스트는 그래프의 연결 관계를 linkedlist로 만들어 보여주는 것이다. 그러기 위해선 vertex를 value로, node 사이의 edge를 pointer 식으로 구성해 보여준다. 리스트의 헤더는 배열을 이용해 노드 번호를 오름차순으로 정렬하기 때문에 vertex에 대한 접근을 보다 빠르게 할 수 있다.
    
  • 방향이 있는 그래프
    
  • 방향이 없는 그래프
  • 접근은 배열 처럼, adj[1][0]은 2 이다. 순서는 의미가 없다.
  • 장점은 인접 행렬과 달리 연결된 노드에 대한 정보만 저장을 해 edge의 개수에 비례하는 메모리만 차지한다.

Hash Table

• 해시 테이블은 배열과 비슷한 형태로 O(1)의 시간 복잡도를 대부분 가지고 있다. 하지만 상황에 따라 최악의 경우인 O(n)을 겪을 수 있는데...
  1. 같은 키에 너무 많은 요소들이 해시 되어 있으면 이 키를 전부다 뒤져봐야 해서 많은 시간이 걸린다. O(n).
  2. 해시 테이블이 로드밸런스(Load Balance)를 초과한 경우, 더 큰 테이블을 만들어 일일이 다시 추가를 해줘야 한다.
• 하지만 평균적으로 O(1)인 이유는
  1. 같은 키에 너무 많은 요소들이 저장되어 있는 것은 매우 드문 경우이고 좋은 해시 함수를 고르면 로드 밸런스의 초과도 없다.

Summary

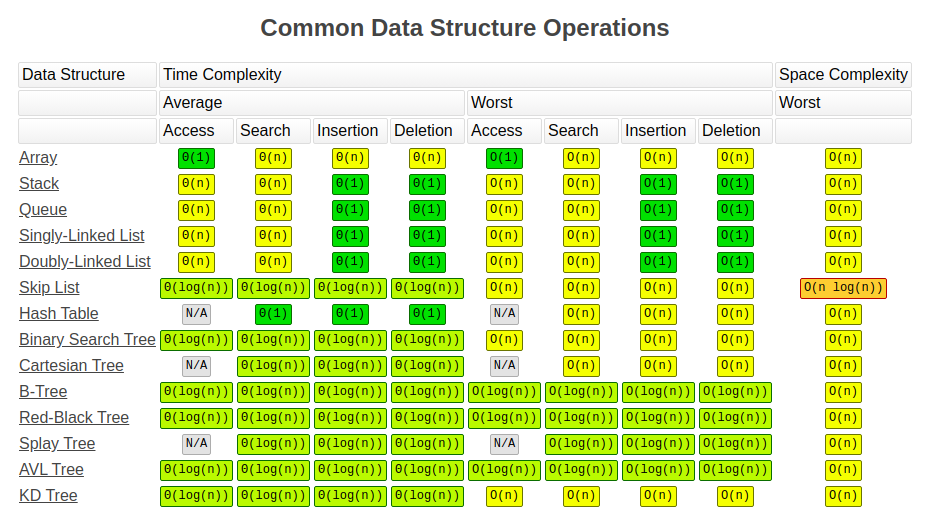
참조 - https://www.bigocheatsheet.com/

https://sarah950716.tistory.com/12

https://adrianmejia.com/data-structures-for-beginners-graphs-time-complexity-tutorial/#Matrix.addVertex

CodeStates