0-1 Knapsack Problem

0-1 Knapsack Problem 이란?

• n개의 물건과 각 물건 i의 무게 wi와 가치 vi가 주어지고, 배낭의 용량은 C일 때, 배낭에 담을 수 있는 물건의 최대 가치를 찾는 문제이다.

• 단, 배낭에 담은 물건의 무게의 합이 C를 초과하지 말아야 하고, 각 물건은 1개씩만 있다.

이런 knapsack Problem을 해결하는 방법은 다음과 같다.

1. 모든 경우은 수를 넣어보는 방법

2. 가격이 높은 보석, 혹은 (가격/무게) 의 값이 제일 높은 보석부터 먼저 골라서 넣는 방법

3. DP -> 다이나믹 프로그래밍을 통해서 푸는 방법

이렇게 3가지가 있는데 여기서는 3번 아이디어로 풀어보도록 하자.

이 방법을 위해서는 최적의 원리가 성립되는지 확인해야 하는데,

이때, 최적의 원리란? "어떤 문제의 입력사례의 최적해가 그 입력사례를 분할한 부분사례에 대한 최적해를 항상 포함하고 있으면, 그 문제에 대하여 최적의 원리가 성립한다." 이다.

과연, 이 문제에서 이 원리가 성립할까? 집합 A를 n개의 아이템들 중에서 최적으로 고른 부분집합이라고 하자.

• 집합 A가 n번째 아이템을 포함하고 있지 않다면, A는 n번째 보석을 뺀 나머지 n-1개의 보석들 중에서 최적으로 고른 부분집합과 같다.

• 집합 A가 n번째 보석을 포함하고 있다면, A에 속한 보석들의 총 가격은 n-1개의 보석들 중에서 최적으로 고른 가격의 합에다가 보석 n의 가격을 더한 것과 같다.

위 얘기를 의사코드로 표현해보자면 다음과 같다.

for i = 1 to n {
	for w = 1 to C { // w는 배낭의 (임시) 용량
		if ( wi > w ) // 물건 i의 무게가 임시 배낭 용량을 초과하면
			K[i,w] = K[i-1,w]
		else // 물건 i를 배낭에 담지 않을 경우와 담을 경우 고려
			K[i,w] = max{K[i-1,w], K[i-1,w-wi]+vi}
	}
}
return K[n,C]

K[i,w]란 i개의 아이템이 있으며 배낭의 무게 한도가 w일때의 최적의 이익을 말한다.
그리고 이때, i번째 아이템의 무게가 배낭의 한도 보다 무거운 경우 i번째 아이템을 뺀 i - 1개의 보석들을 가지고 구한 전 단계의 최적값을 그대로 가져온다.

그게 아니라면 i번째 아이템을 위해 i번째 보석만큼의 무게를 비웠을 때의 최적값의 i번째 보석의 가격을 더한 값 or i - 1개의 보석을 가지고 구한 전 단계의 최적값 중 큰 것을 선택한다.

위 알고리즘을 한 번 수행해보자.

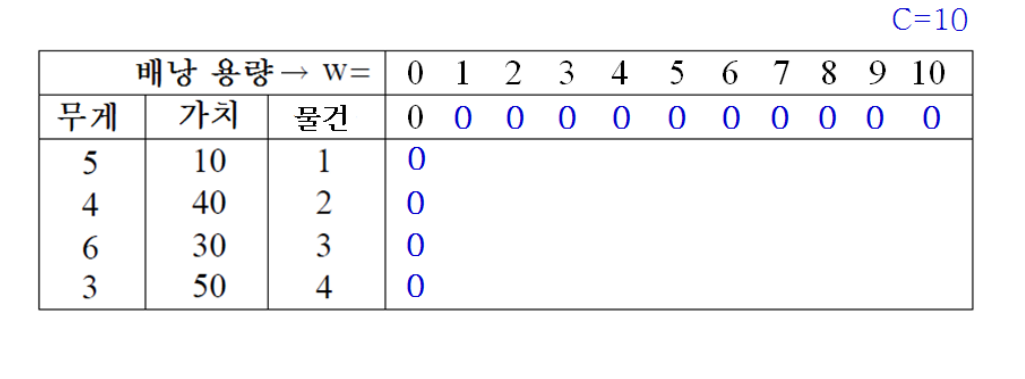
1. 아래와 같이 배열의 0번 행과 0번 열의 각 원소를 0으로 초기화한다.
   

2. 아래의 그림은 물건 1번째 아이템까지 있다는 가정하에 배낭의 무게가 w일때의 최적의 이익을 나타낸 그림이다. w가 0 ~ 4까지는 물건을 담을 수 없으므로 0이지만 w가 5부터는 1번째 아이템을 담을 수 있기때문에 1을 10이 되는 모습을 볼 수 있다.
   

3. 아래의 그림은 물건 2번째 아이템까지 있다는 가정하에 배낭의 무게가 w일때의 최적의 이익을 나타낸 그림이다.
   

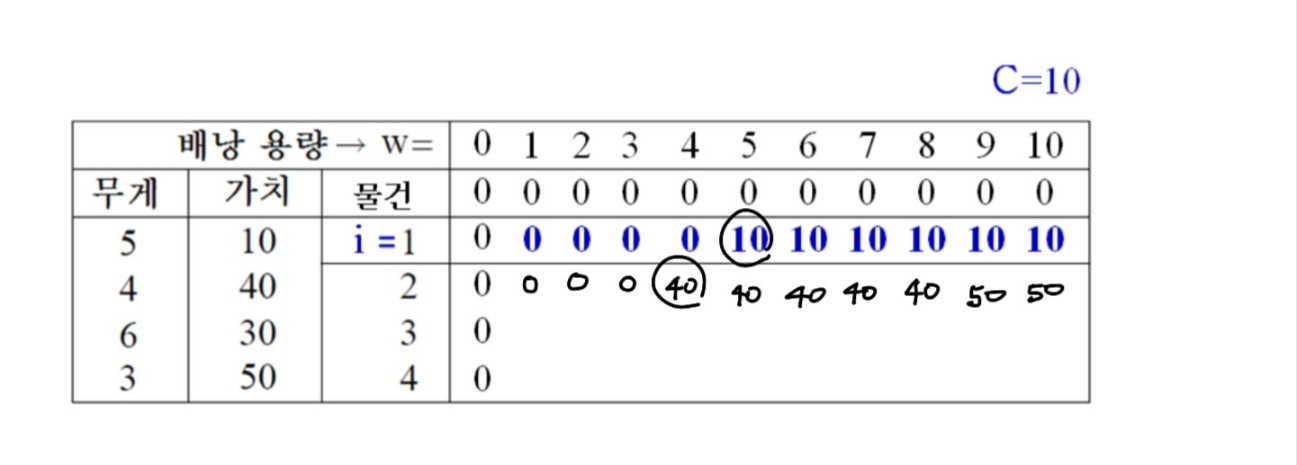
1 ~ 3까지의 경우에는 배낭에 넣을 수 있는 아이템이 없기때문에 0이 된다. 4부터는 아이템의 가치가 40인 물건이 있으므로 40이고 5부터의 경우에는 바로 윗 행의 것과 윗 행에서 아이템의 무게를 뺀 위치에 있는 값에서 + 2번째 아이템을 더한 값과 비교해서 나온 40인 물건을 더한다. 따라서, w가 8인경우까지는 40이 나오고 9부터는 1번째 두번째 아이템을 더 할 수 있기때문에 기존 40과 50을 비교하여 50이 8, 9, 10 열에 들어가게 된다.

4. i = 3, i = 4도 이러한 수행을 마친 결과 다음과 같은 결과가 나온다.

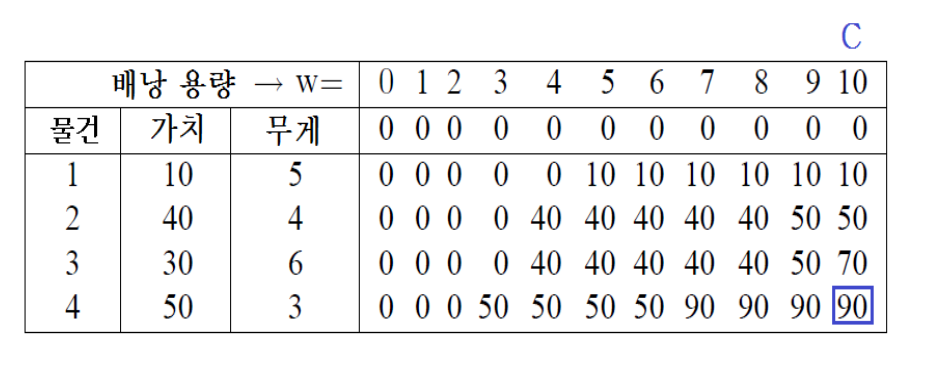
이를 C언어로 바꾸면 다음과 같다.

#include <stdio.h>
#define MAX 100

int k[MAX][MAX]; // 2차원 배열

// 두배열의 0값은 사용하지 않는다 1 ~ 4까지의 인덱스만 사용.
int wt[5] = {0,5,4,6,3}; // 각 보석의 무게
int val[5] = { 0,10,40,30,50 }; // 각 보석의 가치

int max(int a, int b) { // 두 수중에서 최대 값을 return 하는 함수 max
	if (a > b) {
		return a;
	}

	else {
		return b;
	}
}

int main() {
	int w = 10; // 가방의 무게
	int result = 0;
	int save; // 2, 4 가방의 무게

	// k 배열 초기화
	for (int i = 0; i <= 4; i++) {
		k[i][0] = 0;
	}

	for (int j = 0; j <= w; j++) {
		k[0][j] = 0;
	}


	for (int i = 1; i <= 4; i++) {
		for (int j = 1; j <= w; j++) {
			if (wt[i] > j) {
				k[i][j] = k[i - 1][j];
			} // 배낭의 무게한도보다 아이템의 무게가 큰 경우 이전 행에서 같은 배낭의 무게한도에서의 값을 대입

			else {
				k[i][j] = max(k[i - 1][j], k[i - 1][j - wt[i]] + val[i]);
			} // 그게 아닌 경우 같은 배낭 무게 한도에서 이전 행에서 구한 값과 
			// 이전 행에서의 현재 배낭 무게한도에서 현재 아이템의 무게를 뺀열에 해당하는 값과 현재 아이템의 가치를 더한 값을 비교 후 더 큰 값을 대입
		}
	}	


	printf("10kg 가방에 담을 수 있는 최대가치 : %d\n", k[4][w]); 
	// 결국 최대가치는 k[4][10]이 최대가치이다. 왜냐하면 4번째 아이템까지의 아이템을 골라 무게 10이내로 담을 수 있는 최대가치이기 때문에.
	
	// 최대가치의 조합
	printf("가방에 담은 아이템의 조합은 : ");
	for (int i = 4; i > 0 && k[i][10] != 0; i--) {
		if (k[i][w] != k[i - 1][w]) {
			printf("%d ", i);
			w -= wt[i - 1];
		}
	}
	printf("\n");

	return 0;
}