Vertex Covering Problem (정점 커버 문제)

정점 커버 (Vertex Cover) 문제

주어진 그래프 G = (V,E)에서 각 선분의 양 끝점들 중에서 적어도 하나의 끝점을 포함하는 점들의 집합들 중에서 최소크기의 집합을 찾는 문제이다.

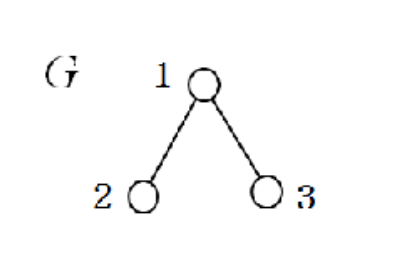
다음 그래프 G에서는 {1,2,3}, {1,2}, {1}, {2,3}이 각각 정점 커버가 될 수 있다.

하지만, {2} 나 {3}은 될 수 없다. 왜냐하면 {2}의 경우에는 선분 (1,3)을 포함할 수 없고 {3}의 경우 선분 (1,2)를 포함할 수 없기 때문이다.

그리고 이 중에서 최소크기의 집합은 {1} 이므로 우리가 찾는 정답은 {1}이다.

이와 같이 설명한 방법은 정점을 선택하는 방법이고, 다른 방법으로는 선분을 선택하는 방법이 있다.

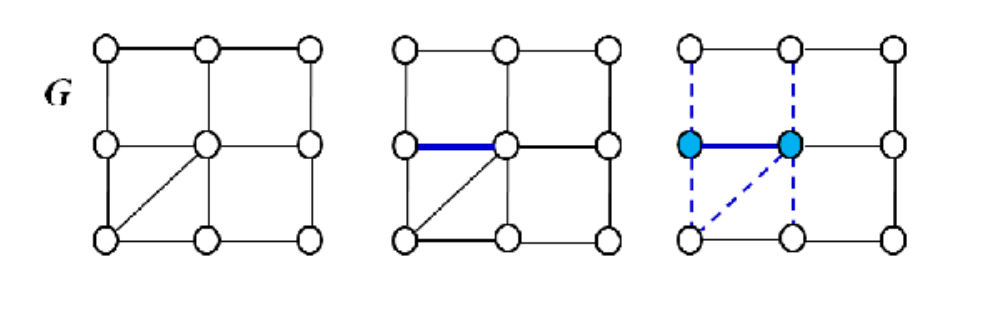
그림처럼 하나의 선분이 선택되는 경우 두 선분의 정점과 인접하는 선분은 정적 커버를 위해 선택되지 않는다.

이러한 방식으로 선분을 선택하다가 더 이상 선분을 추가 할 수 없을 경우 중단한다. 이렇게 선택된 선분의 집합을 극대 매칭이라고 한다.

의사코드는 다음과 같다.

입력: 그래프 G=(V,E)
출력: 정점 커버
1. 입력 그래프에서 극대 매칭 M을 찾는다.
2. return 매칭 M의 선분의 양 끝점들의 집합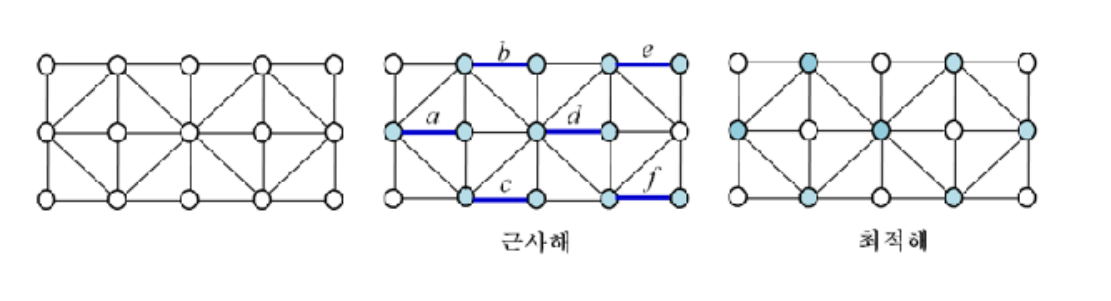

위 그림의 결과를 의사코드로 풀면 다음과 같다 극대매칭으로서 선분 a,b,c,d,e,f가 선택되고 근사해의 값은 12개의 점으로 구성된다.