Chained Matrix Multiplication

연속 행렬 곱셈 (chained Matrix Multiplication) 문제는 연속된 행렬들의 곱셈에 필요한 원소간에 최소 곱셈의 횟수를 찾는 문제이다.

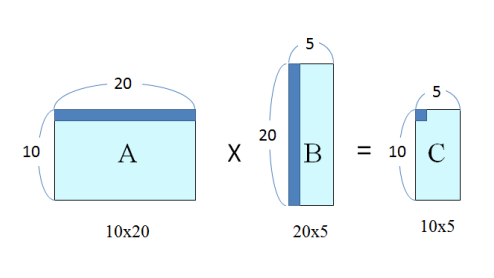
예를 들어, 위와 같이 두 개의 행렬을 곱하는 경우, 10 x 20 행렬 A와 20 x 5 행렬 B를 곱하는데 원소 간의 곱셈 횟수는 10 x 20 x 5 = 1000이다.

또 다른 예시로, 다음과 같이 세 개의 행렬을 곱하는 경우가 있다.

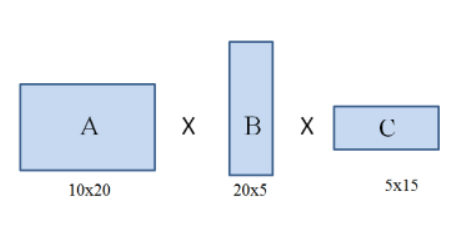
이 경우 A x B x C 의 형태는 (A x B) x C , A x (B x C) 두 가지 형태로 결합이 가능하다.

1. (A x B) x C = AB x C
   (A x B) = 10 x 20 x 5 = 1000 -> AB
   AB x C = 10 x 5 x 15 = 750
   곱셈의 횟수 -> 1750

2. A x (B x C) = A x BC
   (B x C) = 20 x 5 x 15 = 1500 -> BC
   A x BC = 10 x 20 x 15 = 3000
   곱셈의 횟수 -> 4500

그래서 A와 B의 곱을 먼저 진행후 AB와 C의 곱을 진행하는 것이 곱셈의 횟수가 더 적게 나온다는 것을 알 수 있었다.

알고리즘의 의사코드는 다음과 같다.

MatrixChain
입력: 연속된 행렬 A1\*A2\*...\*An,
출력: 입력의 행렬 곱셈에 필요한 원소 간의 최소 곱셈 횟수
for i = 1 to n
  C[i,i] = 0
for L = 1 to n-1 {	//L은 부분문제의 크기를 조절하는 인덱스
  for i = 1 to n-L {
    j = i + L
    C[i,j] = ∞
    for k = i to j-1 {
      temp = C[i,k] + C[k+1,j] + d(i-1)dkdj
      if (temp < C[i,j])
        C[i,j] = temp
    }
  }
}
return C[1,n]

이 의사코드 다음과 예시를 통해 이해해보자.

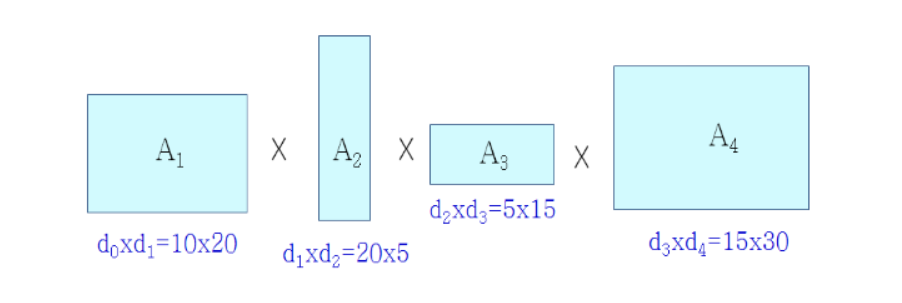
먼저, C[1,1] = C[2,2] = C[3,3] = C[4,4] = 0으로 초기화한다.

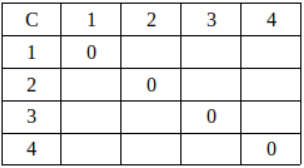
Line 6 : L이 1부터 n-1 = 4-1 = 3까지 변하고, 각각의 L값에 대해, i가 변화, C[i,j]를 계산.
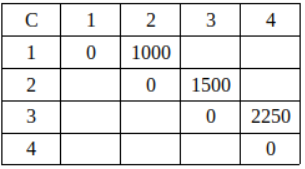
L = 1일 때, i는 1부터 n-L = 4-1 = 3까지 변한다.

• i = 1이면, j = i+L = 1+1 = 2, C[1,2] = ∞,
  temp = C[1,1] + C[2,2] + d0d1d2 = 0 + 0 + (10x20x5) = 1000
  temp = 1000 < C[1,2] = ∞, C[1,2] = 1000

• i = 2이면, j = i+L = 2+1 = 3, C[2,3] = ∞
  temp = C[2,2] + C[3,3] + d1d2d3 = 0 + 0 + (20x5x15) = 1500
  temp = 1500 < C[2,3] = ∞, C[2,3] = 1500

• i = 3이면, j = i+L = 3+1 = 4, C[3,4] = ∞
  temp = C[3,3] + C[4,4] + d2d3d4 = 0 + 0 + (5x15x30) = 2250
  temp = 2250 < C[3,4] = ∞, C[3,4] = 2250

L = 2일 때, i는 1부터 n-L = 4-2 = 2까지 변한다.

• i = 1이면, j = i+L = 1+2 = 3, C[1,3] = ∞

  • k = 1일 때, temp = C[1,1] + C[2,3] + d0d1d3 = 0 + 1500 + (10 x 20 x 15) = 4500
    temp = 4500 < C[1,3] = ∞, C[1,3] = 4500

    A2xA3 = 1500, A1xA2A3 = 3000 + 1500

  • k = 2일 때, temp = C[1,2] + C[3,3] + d0d2d3 = 1000 + 0 + (10x5x15) = 1750
    temp = 1750 < C[1,3] = 4500, C[1,3] 1750

    A1xA2 = 1000, A1A2xA3 = 1000 + 750

• i = 2이면, j = i+L = 2+2 = 4, C[2,4] = ∞

  • k = 2일 때, temp = C[2,2] + C[3,4] + d1d2d4 = 0 + 2250 + (20x5x30) = 5250
    temp = 5250 < C[2,4] = ∞, C[2,4] = 5250

    A3xA4 = 2250, A2xA3A4 = 3000 + 2250

  • k = 3일 때, temp = C[2,3] + C[4,4] + d1d3d4 = 1500 + 0 + (20x15x30) = 10500
    temp = 10500 > C[2,4] = 2250, C[2,4] = 5250

    A2xA3 = 1500, A2A3xA4 = 9000 + 1500

L = 3일 때, i는 1부터 n-L = 4-3 = 1까지 변한다.(i=1일때만 수행)

• i = 1이면, j = i+L = 1+3 = 4, C[1,4] = ∞

  • k = 1일 때, temp = C[1,1] + C[2,4] = d0d1d4 = 0 + 5250 + (10x20x30) = 11250
    temp = 11250 < C[1,4] = ∞, C[1,4] = 11250

    A2xA3xA4 = 5250, A1xA2A3A4 = 6000

  • k = 2일 때, temp = C[1,2] + C[3,4] = d0d2d4 = 1000 + 2250 + (10x5x30) = 4750
    temp = 4750 < C[1,4] = ∞, C[1,4] = 4750

    A1xA2 = 1000, A3xA4 = 2250, (A1A2)x(A3A4) = 1000 + 1500 + 2250 = 4750

  • k = 3일 때, temp = C[1,3] + C[4,4] = d0d3d4 = 1750 + 0 + (10x15x30) = 6250
    temp = 6250 > C[1,4] = 4750, C[1,4] = 4750

    A1xA2 = 1000, A3xA4 = 2250, (A1A2)x(A3A4) = 1750 + 4500 = 6250

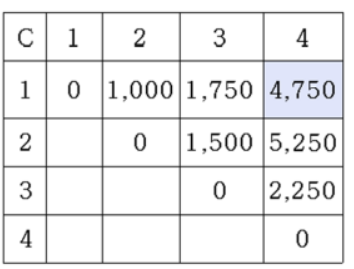
C[1,4]= 4750을 반환한다.

이를 C언어 코드로 나타내면 다음과 같다.

#include <stdio.h>
#define MAX 100

int arr[MAX][MAX];
int INF = 1000000;
int answer[3];

int chainMatrixMulitiply(int num) { // 행렬 곱셈 함수
	int d[MAX];

	d[0] = 10, d[1] = 20, d[2] = 5, d[3] = 15, d[4] = 30; // d0 ~ d4까지의 값

	for (int L = 0; L < num; L++) { 

		for (int i = 1; i <= num - L; i++) {
			int j = i + L;
			
			if (j == i) { // arr[1][1] 과 같은 요소는 모두 0으로 처리
				arr[i][j] = 0;
				continue;
			}

			arr[i][j] = INF; // i j 의 초기값은 무한으로 설정

			for (int k = i; k <= j - 1; k++) { // 기존의 i에서 j까지의 행렬의 곱의 횟수와 (Ai X Ak) + (Ak+1 X Aj) 의 곱의 횟수를 비교하고
				// 더 적은 값을 arr[i][j]에 넣어준다.
				int temp = arr[i][k] + arr[k + 1][j] + d[i - 1] * d[k] * d[j];
				if (arr[i][j] > temp) {
					arr[i][j] = temp;
					answer[0] = i;
					answer[1] = k;
					answer[2] = j; // (Ai X Ak) + (Ak + 1 X Aj)의 행렬 순서를 출력하기 위해 i k j값을 저장한다.
				}
			}
		}
	}

	return arr[1][4];
}

int main() {
	int num = 4; // 총 행렬의 수
	int result = chainMatrixMulitiply(num);

	// 행렬의 결과 출력
	for (int i = 1; i <= num; i++) {
		for (int j = 1; j <= num; j++) {
			printf("%d  ", arr[i][j]);
		}
		printf("\n");
	}

	printf("\n\n");
	
	// 곱의 최적해 출력
	printf("A1 X A2 X A3 X A4 의 최적해 : %d\n\n", result);

	// 행렬의 곱셈 순서 출력
	printf("행렬의 곱셈 순서 : ");
	printf("(");
	for (int i = 1; i <= answer[1]; i++) {
		if (i == answer[1]) {
			printf("A%d", i);
			continue;
		}
		printf("A%d X ", i);
	}
	printf(")");

	printf(" X ");

	printf("(");
	for (int i = answer[1] + 1; i <= answer[2]; i++) {
		if (i == answer[2]) {
			printf("A%d", i);
			continue;
		}

		printf("A%d X ", i);
	}
	printf(")");
	return 0;
}