Floyd-Warshall (플루이드 알고리즘)

모든 쌍 최단 경로 존재여부 찾아내는 WarShall의 알고리즘에서 Floyd가 변형시켜서 모든 쌍의 최단 경로를 찾아내는 알고리즘을 만들어냈다.

Floyd Algorithm의 아이디어

1. 부분문제들을 찾는다.

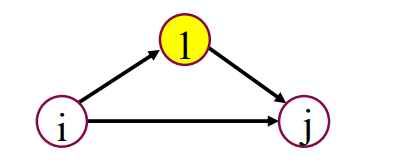
위 그림을 예시로 들었을때, 점 i에서 j까지의 최단 경로를 찾으려면 2가지 경로, 점 i에서 j로 직접가는 경로와 점 1을 경유하는 경로 중에서 짧은 것을 선택하면 된다.

2. 모든 가능한 점들로 고려하면서 모든 쌍의 최단 경로의 거리를 계산한다.

경유 가능한 점들을 점 1로부터 시작하여, 점 1과 2, 그 다음엔 점 1, 2, 3으로 하나씩 추가하여, 마지막에는 점 1∼(n-2)까지의 모든 점을 경유 가능한 점들로 고려하면서, 모든 쌍의 최단경로의 거리를 계산한다.

이 아이디어의 의사코드는 다음과 같다.

입력: 2차원 배열 D, 단 D[i,j]=간선(i,j)의 가중치, 만일 간선 (i,j)이 존재하지 않는다면, 
      D[i,j]= inf, 모든 i에 대하여 D[i,j]=0이다.
출력: 모든 쌍의 최단 경로의 거리를 저장한 2차원 배열 D
1. for k = 1 to n
2. 	for i=1 to n (단 i!=k)
3. 		for j=1 to n (단, j!=k,j!=i)
4. 			D[i,j] = min{D[i,k]+D[k,j],D[i,j]}

수행과정

다음과 같은 예시가 있다.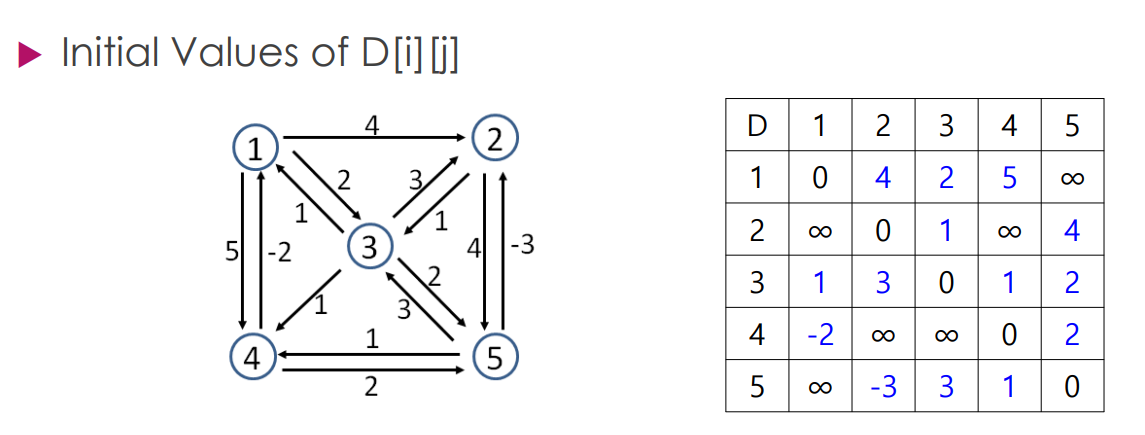

K -> 무조건 지나는 점.
배열 D의 원소들이 K가 1부터 5까지 증가함에 따라서 갱신된다.
즉, i -> 1 -> j 가 기존의 i -> j의 경로보다 더 적은 비용이 드는 경우 갱신

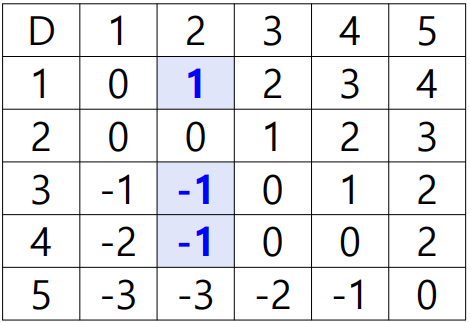
K가 1일 경우를 예시로 들어보면

D[2,3] = min{D[2,3], D[2,1]+D[1,3]} = min{1, ∞+2} = 1
D[2,4] = min{D[2,4], D[2,1]+D[1,4]} = min{∞, ∞+5} = ∞
D[2,5] = min{D[2,5], D[2,1]+D[1,5]} = min{4, ∞+∞} = 4
D[3,2] = min{D[3,2], D[3,1]+D[1,2]} = min{3, 1+4} = 3
D[3,4] = min{D[3,4], D[3,1]+D[1,4]} = min{1, 1+5} = 1
D[3,5] = min{D[3,5], D[3,1]+D[1,5]} = min{2, 1+∞} = 2
D[4,2] = min{D[4,2], D[4,1]+D[1,2]} = min{∞, -2+4} = 2
D[4,3] = min{D[4,3], D[4,1]+D[1,3]} = min{∞, -2+2} = 0
D[4,5] = min{D[4,5], D[4,1]+D[1,5]} = min{2, -2+∞} = 2
D[5,2] = min{D[5,2], D[5,1]+D[1,2]} = min{-3, ∞+4} = -3
D[5,3] = min{D[5,3], D[5,1]+D[1,3]} = min{3, ∞+2} = 3
D[5,4] = min{D[5,4], D[5,1]+D[1,4]} = min{1, ∞+5} = 1

그래서 최종적으로는 다음과 같은 형태가 된다.

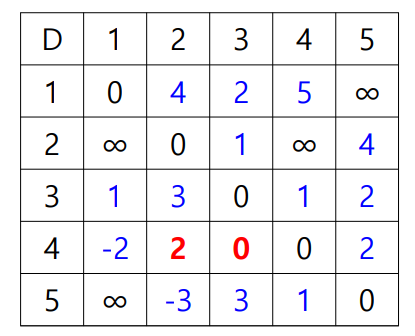
이와 같은 형식으로 K가 5까지 진행하면, 최종적으로 다음과 같은 형태가 된다.

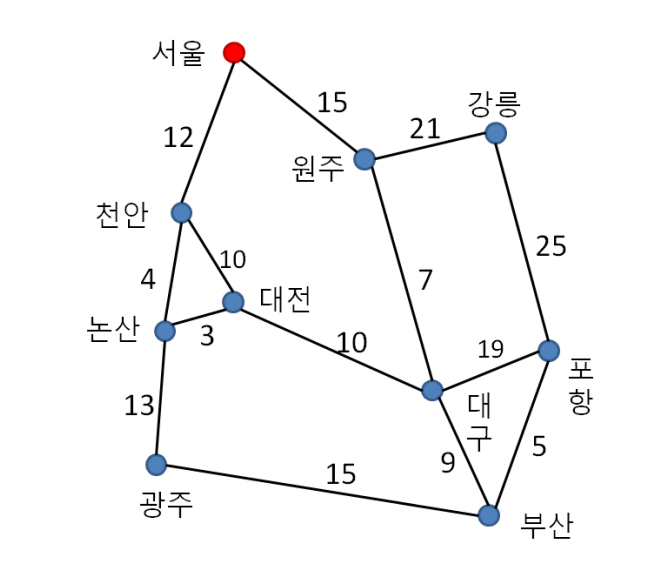
다음과 각 지역에 대한 최소거리를 플루이드와 다익스트라를 비교한 결과를 C언어로 다음과 같이 나타내보았다.

#include <stdio.h>
#define MAX 100
#define LOCAL_COUNT 10

int INF = 100000000;

int map[MAX][MAX] = {
	{0,12,15,INF,INF,INF,INF,INF,INF,INF}, // 서울
	{12,0,INF,INF,4,INF,10,INF,INF,INF}, // 천안
	{15,INF,0,21,INF,INF,INF,7,INF,INF}, // 원주
	{INF,INF,21,0,INF,INF,INF,INF,INF,25}, // 강릉
	{INF,4,INF,INF,0,13,3,INF,INF,INF}, // 논산
	{INF,INF,INF,INF,13,0,INF,INF,15,INF}, // 광주
	{INF,10,INF,INF,3,INF,0,10,INF,INF}, // 대전
	{INF,INF,7,INF,INF,INF,10,0,9,19}, // 대구
	{INF,INF,INF,INF,INF,15,INF,9,0,5}, // 부산
	{INF,INF,INF,25,INF,15,19,INF,5,0} }; // 포항

int visited[10]; // 방문 여부
char local[10][MAX] = { "서울", "천안", "원주", "강릉", "논산", "광주", "대전", "대구", "부산", "포항" }; // 지역

int dijkstra_d[10]; // 다익스트라의 최단거리 배열
int floyd_d[MAX][MAX]; // 플루이드의 최단거리 배열

int getSmallIndex() { // 현재 방문하지 않은 정점중 가장 짧은 거리에 있는 정점을 고르는 함수
	int min = INF;
	int index = 0;

	for (int i = 0; i < LOCAL_COUNT; i++) {
		if (dijkstra_d[i] < min && !visited[i]) {
			min = dijkstra_d[i];
			index = i;
		}
	}

	return index;
}
void init() { // 다익스트라 관련 배열 초기화
	for (int i = 0; i < LOCAL_COUNT; i++) {
		dijkstra_d[i] = 0;
		visited[i] = 0;
	}
}

void dijkstra(int start) {
	// 시작점 체크
	init();
	visited[start] = 1;
	for (int i = 0; i < LOCAL_COUNT; i++) {
		dijkstra_d[i] = map[start][i];
	} // 시작점으로부터의 다른 지역간의 거리를 거리배열안에 저장

	for (int i = 0; i < LOCAL_COUNT - 2; i++) { // 처음과 끝은 할 필요가 없기때문에
		int current = getSmallIndex(); // 현재 distance 중 가장 짧은 distance를 선택

		visited[current] = 1; // 선택한 현재 지점에서 방문여부 체크

		for (int j = 0; j < LOCAL_COUNT; j++) {
			if (!visited[j]) {
				if (dijkstra_d[current] + map[current][j] < dijkstra_d[j]) {
					// 현재 지점을 거쳐서 방문하지 않은 한 지점에 도달한 거리와 현재 거리배열안에 있는 그 지점에 도달한 거리를 비교
					dijkstra_d[j] = dijkstra_d[current] + map[current][j];
					// 만약 현재 지점을 거쳐서 간 경우가 빠른 경우 거리배열안에 이 경우를 넣고 거리배열을 갱신해준다.
				}
			}
		}
	}


	for (int i = 0; i < LOCAL_COUNT; i++) {
		printf("%3d ", dijkstra_d[i]);
	}
}

void floydWarshall() {

	// floyd 배열에 map 정보를 넣어준다.
	for (int i = 0; i < LOCAL_COUNT; i++) {
		for (int j = 0; j < LOCAL_COUNT; j++) {
			floyd_d[i][j] = map[i][j];
		}
	}

	// k = 거쳐가는 노드
	for (int k = 0; k < LOCAL_COUNT; k++) {
		// i = 출발 노드
		for (int i = 0; i < LOCAL_COUNT; i++) {
			// j = 도착 노드
			for (int j = 0; j < LOCAL_COUNT; j++) {
				if (floyd_d[i][k] + floyd_d[k][j] < floyd_d[i][j]) { // i에서 j로 가는 비용 vs i에서 k를 걸쳐서 j로 가는 비용
					floyd_d[i][j] = floyd_d[i][k] + floyd_d[k][j];
				} 
			} // 비교했을때 후자가 더 작은 경우 후자가 더 작은 경우 후자를 floyd_d[i][j]에 대입
		}
	}

	// 결과를 출력합니다.
	for (int i = 0; i < LOCAL_COUNT; i++) {
		for (int j = 0; j < LOCAL_COUNT; j++) {
			printf("%3d ", floyd_d[i][j]);
		}
		printf("\n");
	}
}

int main() {
	printf("지역순서 : ");
	for (int i = 0; i < LOCAL_COUNT; i++) {
		printf("%s ", local[i]);
	}

	printf("\n\n");

	// dijkstra 결과출력
	printf("dijkstra 결과\n");
	for (int i = 0; i < LOCAL_COUNT; i++) {
		dijkstra(i);
		printf("\n");
	}

	printf("\n");

	// floyd 결과출력
	printf("floyd 결과\n");
	floydWarshall();
	return 0;
}