🍀 DFS(Depth-First Search)
이 블로그에서는 탐색 알고리즘 중 DFS(Depth-First Search)와 BFS(Breadth-First Search)를 다룰 것이다. dfs와 bfs는 탐색알고리즘 중 하나로 탐색은 원하는 데이터를 얻기 위해서 특정한 조건을 이용하여 찾는 과정을 의미한다. 이 알고리즘은 특히 Graph 또는 Tree구조에서 자주 다뤄지는 알고리즘이다.
먼저 DFS를 살펴보자. Depth-First Search의미를 그대로 직역해 보면 깊은 곳부터 먼저 탐색이라고 해석할 수 있다. dfs는 재귀함수로 구현할 수 있으며 stack구조로도 구현할 수 있다. stack으로 구현할 수 있는 이유는 재귀함수의 호출(push)은 끝남(pop)이 stack의 특징을 띄기 때문이다. dfs의 동작방식의 이해를 위해 아래 위키피디아에서 가져온 tree구조에서의 dfs 동작방식을 살펴보자.
tree구조에서의 dfs 동작방식
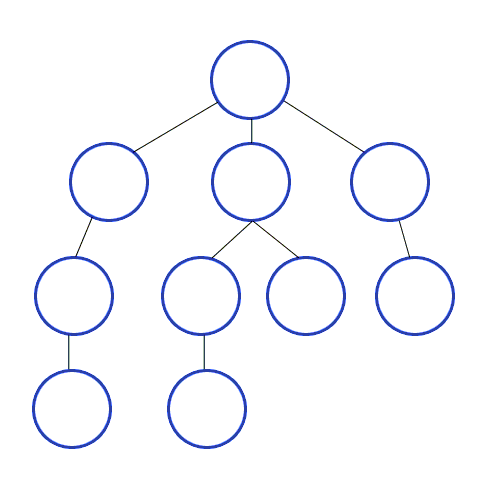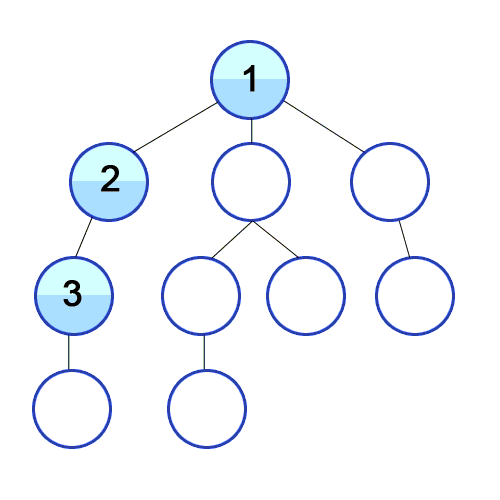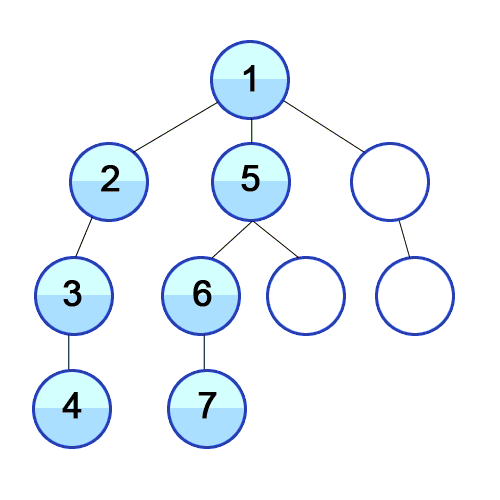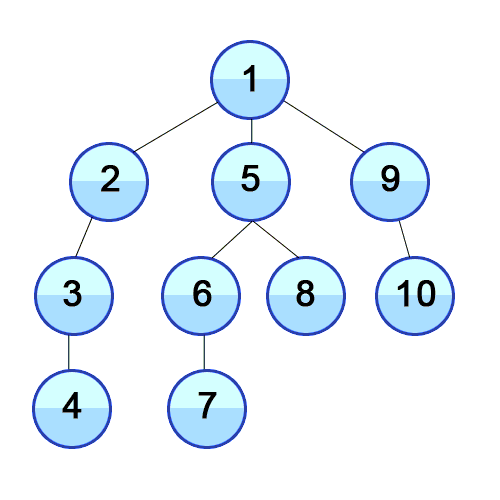
위의 애니메이션을 보면 맨 depth가 가장 큰(가장 하위 노드) 노드까지 탐색하고나서 다음 branch(분기)의 가장 하위 노드를 탐색을 반복하는 것을 알 수 있다. 즉, 현재 branch내의 node를 모두 탐색하고 나서 다음 branch를 모두 탐색한다.
branch(분기)가 이해 안 가는 사람도 있을 듯 하여 그림을 그렸다. 아래 빨간색, 초록색, 보라색 박스에 해당되는 영역 각각을 분기의 subTree라고 한다.
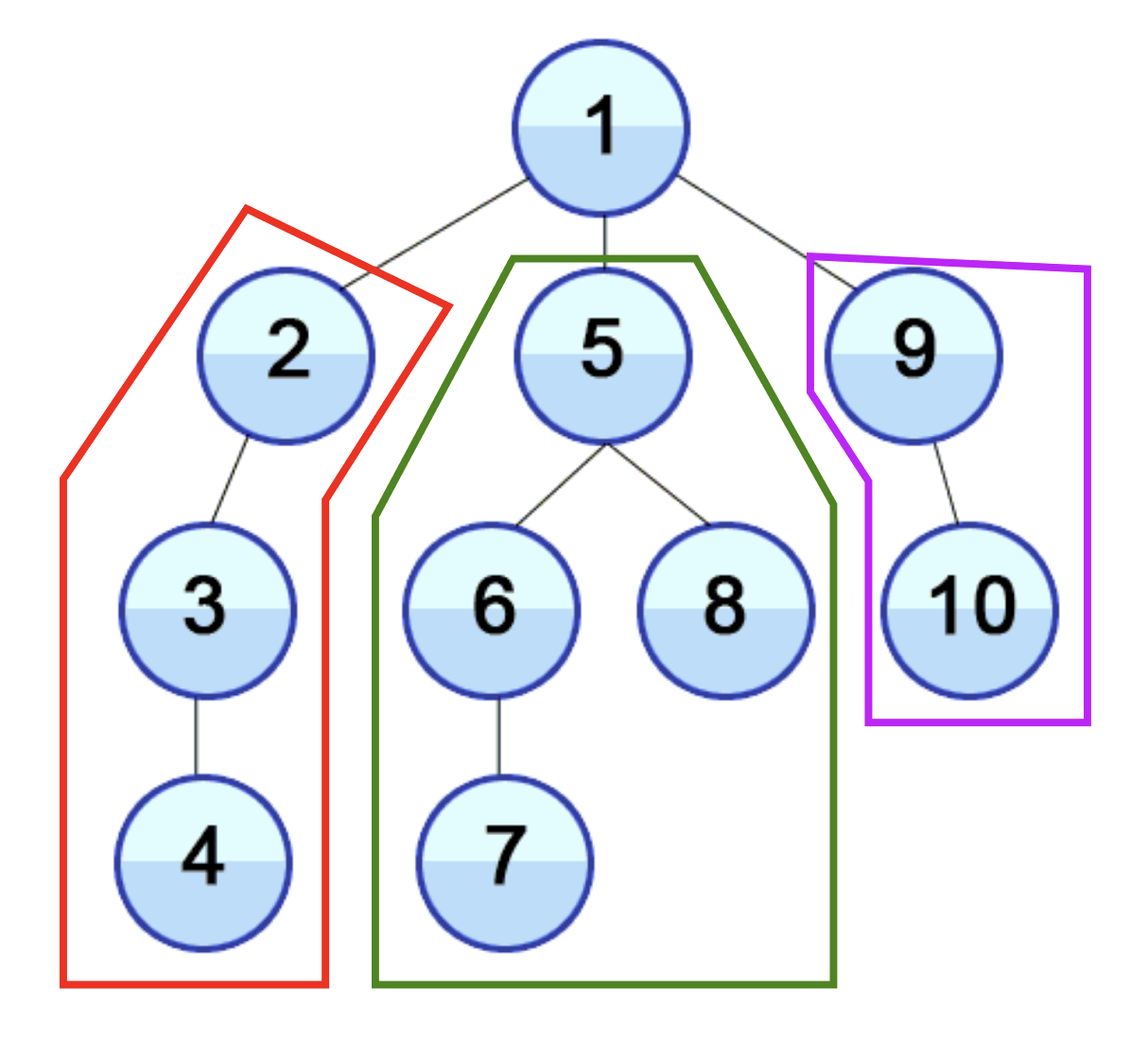
Tree
위에서 언급했듯이 Tree구조에서 순회를 할 때 dfs, bfs알고리즘은 매우 유용해다고 했다. 아래에서는 tree구조에서 dfs 알고리즘에 대해서 설명한다. 탐색할 때 어떤 예시를 들면 좋을까 생각하다가 permutation(순열)로 예시를 들면 좋을 거 같았다.
💡 permutation(순열)
순열은순서는 상관있으며 중복에 상관없이어떤 집합에 대해서 순서를 나열하여 나타날 수 있는 경우의 수이다.
- 트리 순회 중에서도
전위 순회(preorder traverse)에 속하며 전위 순회 외에도중위 순회(inorder traverse)와 후위 순회(postorder traverse)도 있다.
순열의 예시 데이터로 간단하게 [1, 2, 3]을 가지고 할 것이다. 데이터가 커지면 이해하는데 복잡하고 간단한 구조에서 더 어려운 구조로 확장해 나가는 것이 쉽게 공부할 수 있다고 생각하기 때문이다.
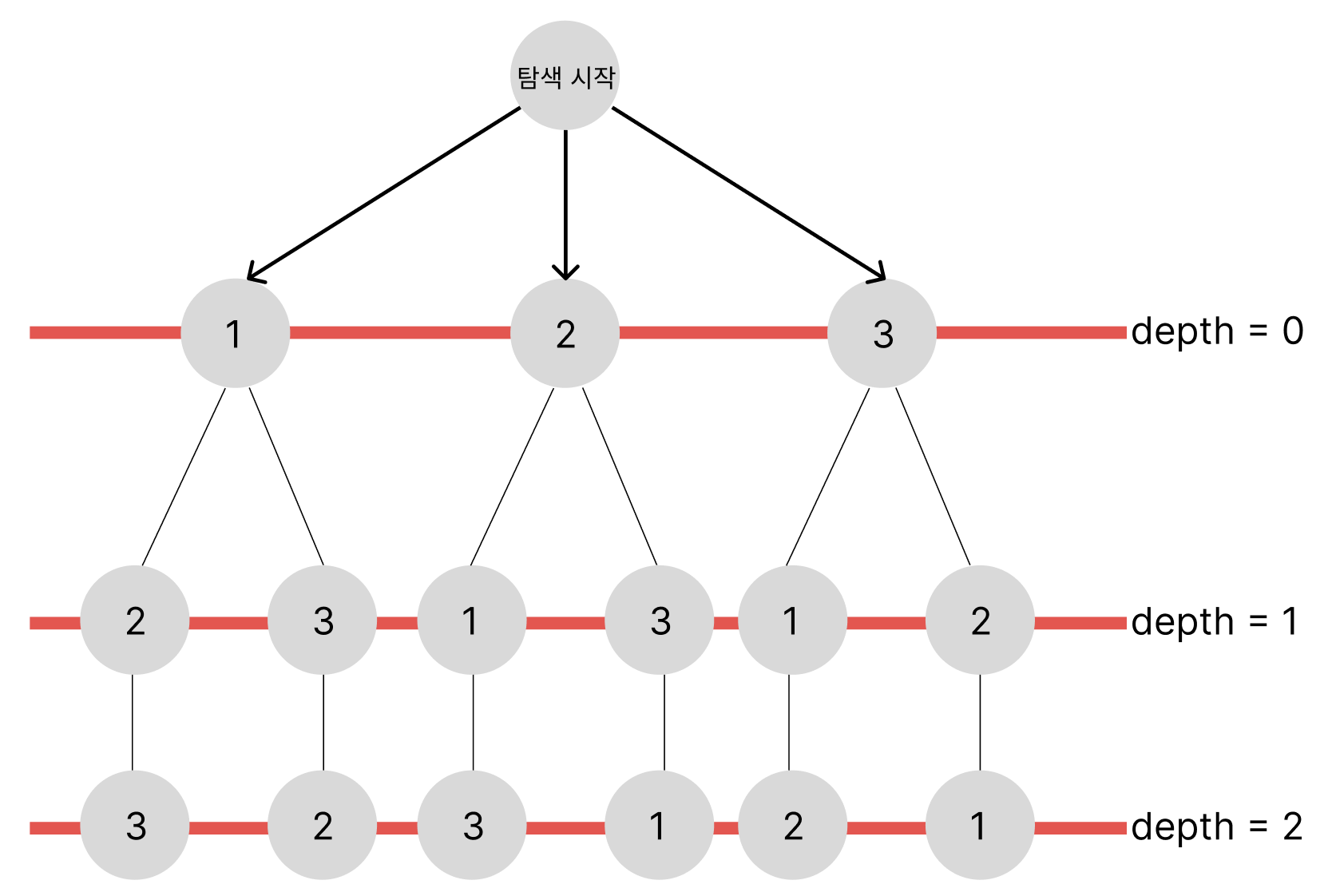
자료를 준비하는 것은 항상 figma로 하는데 복사 붙여넣기 없으면 생각만해도 아찔하다...;;
무튼, 위에서 전위 순회를 통해서 순열을 구할 수 있다고 했는데 탐색되는 순서가 전위 순회가 같아서 말한 것이다(아니면 나중에 알게 될 것이다...??🤔). 코드 구현부에서는 재귀함수로 구현했다.
탐색순서
1️⃣ 1(depth = 0) -> 2(depth = 1) -> 3(depth = 2) -> 3(depth = 1) -> 2(depth = 2) -> 다음 분기(값이 2이며 depth가 0인 노드가 해당되는 부분 tree)2️⃣ 2(depth = 0) -> 1(depth = 1) -> 3(depth = 2) -> 3(depth = 1) -> 1(depth = 2) -> 다음 분기(값이 3이며 depth가 0인 노드가 해당되는 부분 tree)
2️⃣ 3(depth = 0) -> 1(depth = 1) -> 2(depth = 2) -> 2(depth = 1) -> 1(depth = 2) -> Finish
구현
순열을 구하는 방식은 현재 선택한 값을 제외한 집합에서 1개를 선택하는 로직을 반복하는 것이다. 글은 어려우니 예시를 들면 아래와 같다.
📚 순열 동작 예시
1. 집합: [1, 2, 3] 선택: 1 나머지 집합: [2, 3]
2. 집합: [2, 3] 선택: 2 나머지 집합: [3]
3. 집합: [2, 3] 선택: 3 나머지 집합: [2]
======= 👇 다음 branch(분기) =======
4. 집합: [1, 2, 3] 선택: 2 나머지 집합: [1, 3]
5. 집합: [1, 3] 선택: 1 나머지 집합: [3]
6. 집합: [1, 3] 선택: 3 나머지 집합: [1]
======= 👇 다음 branch(분기) =======
7. 집합: [1, 2, 3] 선택: 3 나머지 집합: [1, 2]
8. 집합: [1, 2] 선택: 1 나머지 집합: [2]
9. 집합: [1, 2] 선택: 2 나머지 집합: [1]
시각화를 했으니 동일한 패턴이 보일 것이다. 현재 주어진 집합에서 한 개를 선택하고 나머지 집합은 다음 단계에서 1개를 선택을 위해 구해진다. 즉, 쉽게 말하면 나머지 집합은 다음 함수의 인자 값으로 전달해야 된다는 의미이다.
// permutation code
function getPermutation(arr, select) {
const permutation = [];
const tmpArr = [];
function dfs(partialArr, depth) {
if (tmpArr.length === select) return permutation.push([...tmpArr]);
for (let idx = 0; idx < partialArr.length; idx++) {
tmpArr.push(partialArr[idx]); // 👉🏻 주어진 배열에서 한 개를 선택
dfs([...partialArr.slice(0, idx), ...partialArr.slice(idx + 1)], depth + 1); // 👉🏻 나머지 배열을 넘겨주어 한 개 요소를 선택하게 한다.
tmpArr.pop(); // 트리를 거꾸로 올라올 때 선택된 값은 빼준다.
}
}
dfs([...arr], 0);
return permutation;
}
const testArr = [1, 2, 3];
const permutations = getPermutation(testArr, 3);
console.log("permutations 👉🏻", permutations);주석 안에 이모지 👉와 함께 존재하는 라인이 중요한 부분이다. 테스트를 위해 [1, 2, 3] 중에 3개를 선택하는 것으로 값을 주고 console을 찍어보면 아래와 같이 잘 나온다.
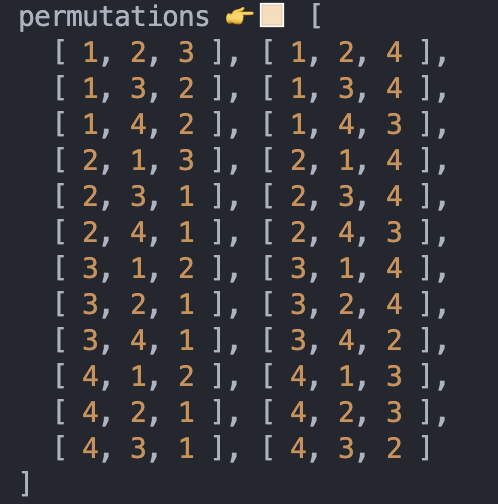
[1, 2, 3, 4]에 대해서 2개만 찍는다면???
const testArr = [1, 2, 3, 4];
const permutations = getPermutation(testArr, 2);
console.log("permutations 👉🏻", permutations);
잘 나온다!!
인접 행렬(Adjacent Matrix)
인접 행렬이란 정점(node 또는 vertex라고 함)들 간의 연결 정보를 행렬로 나타내는 것으로 그래프를 나타내는 방법 중 하나다.
💡 인접 행렬 특징
- 2차원 배열로 나타낼 수 있다.
- 행과 열은 각 노드를 나타낸다.
- 값은 두 정점 사이에 간선(edge)이 존재하는지에 대한 유무이다.(0은 이어져 있지 않음. 1은 이어져 있음)
Ex) [[0, 1, 0, 0]] 👉🏻 0번 노드는 1번 노드와 연결되어 있다.
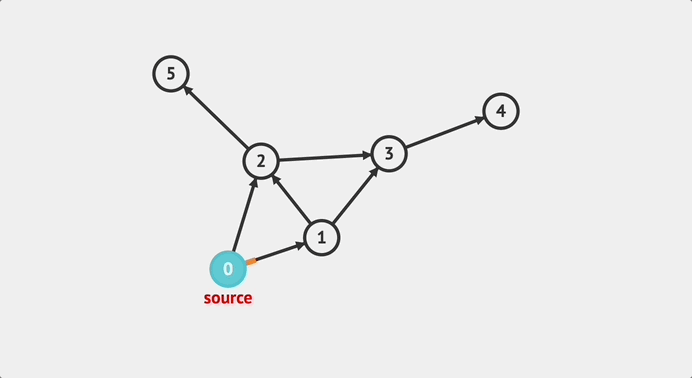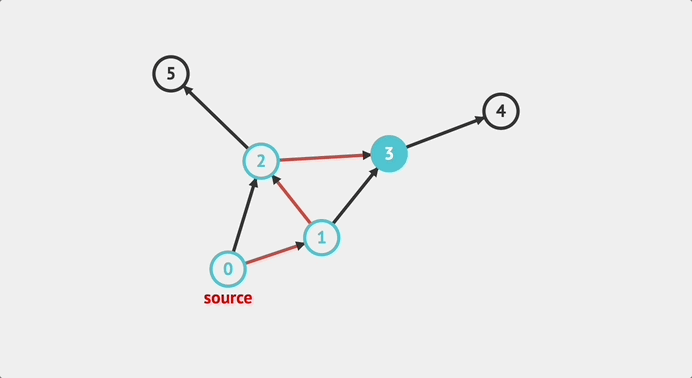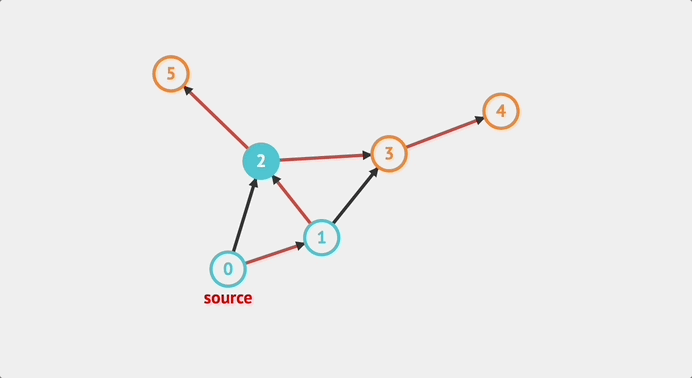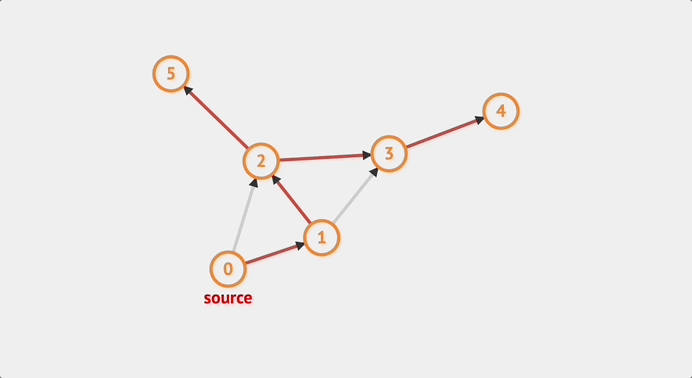
예시를 뭘 들어야할까 하다가 visualalgo에서 제공하는 예시를 사용하기로 했다. 단, 노드 간의 간선이 단방향으로 되어 있어 단방향 그래프 이다.
visual algo에서 edit graph를 이용하면 내가 원하는 값을 추가할 수 있다.
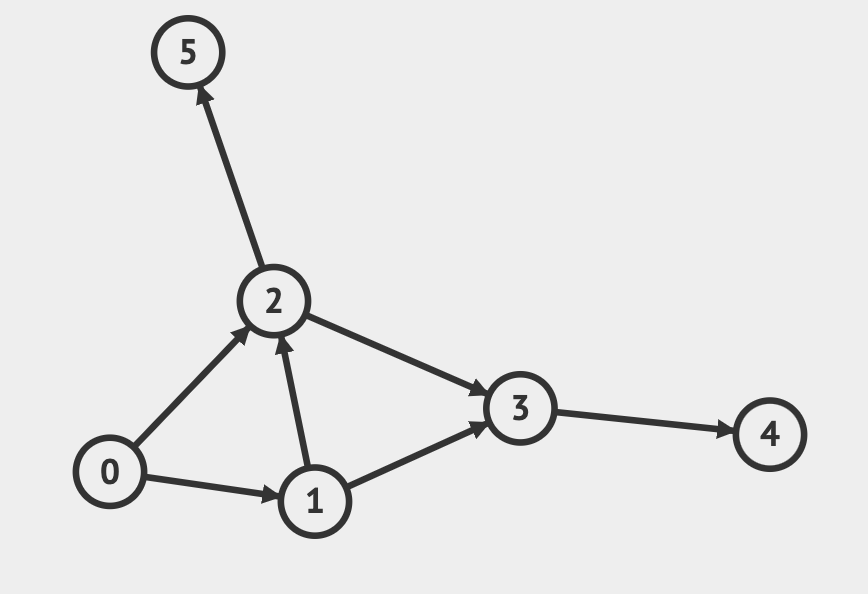
적절한 값을 주어 위의 그래프를 생성했다. 위의 그래프는 인접 행렬로 아래와 같이 표시 할 수 있다.
const graph = [
[0, 1, 1, 0, 0, 0 ],
[0, 0, 1, 1, 0, 0 ],
[0, 0, 0, 1, 0, 1 ],
[0, 0, 0, 0, 1, 0 ],
[0, 0, 0, 0, 0, 0 ],
[0, 0, 0, 0, 0, 0 ]
]위의 그래프를 해석해보자!!
노드간 간선정보를 나타낸 graph해석
연결되어 있다는 것은 간선이 존재한다는 의미이다.
- 0번 노드에 대한 간선 정보: [0, 1, 1, 0, 0, 0 ]
0번 노드는 0번 노드와 연결되어 있지 않다.
0번 노드는 1번 노드와 연결되어 있다.
0번 노드는 2번 노드와 연결되어 있다.
0번 노드는 3번 노드와 연결되어 있지 않다.
0번 노드는 4번 노드와 연결되어 있지 않다.
0번 노드는 5번 노드와 연결되어 있지 않다.
- 1번 노드에 대한 간선 정보: [0, 0, 1, 1, 0, 0 ]
0번 노드는 0번 노드와 연결되어 있지 않다.
0번 노드는 1번 노드와 연결되어 있지 않다.
0번 노드는 2번 노드와 연결되어 있다.
0번 노드는 3번 노드와 연결되어 있다.
0번 노드는 4번 노드와 연결되어 있지 않다.
0번 노드는 5번 노드와 연결되어 있지 않다.... 반복 //
한 번, 탐색 순서를 예측해보자 내가 예측해본 순서는 아래와 같다.
0 -> 1 -> 2 -> 3 -> 4 -> 2번 노드로 돌아감 -> 5 -> 2번을 경유하여 1번 노드로 돌아감 -> 3 -> 1번을 경유하여 0번 노드로 돌아감 -> 2
즉 탐색 순서는 아래와 같다.
0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 3 -> 2
맞나 확인해보면 맞다!!! 아래는 visualalgo에서 gif를 딴 것이다.
구현
const graph = [
[0, 1, 1, 0, 0, 0 ],
[0, 0, 1, 1, 0, 0 ],
[0, 0, 0, 1, 0, 1 ],
[0, 0, 0, 0, 1, 0 ],
[0, 0, 0, 0, 0, 0 ],
[0, 0, 0, 0, 0, 0 ]
]
function dfs (currentNode) {
let routes = '';
const edgeInfo = graph[currentNode];
for (let nextNode = 0; nextNode < edgeInfo.length; nextNode++){
if (edgeInfo[nextNode] === 1 ){
graph[currentNode][nextNode] = 0;
routes += `${nextNode} 👉🏻 ${dfs(nextNode)}` // ⭐️
}
}
return routes;
}
let routes = '0 👉🏻 ' + dfs(0);
routes = routes.slice(0, routes.length - 5)
console.log("탐색 순서", routes);이해를 좀 더 돕기 위해 좀 더 글을 적어봤다.
아래 현재 간선정보에 빨간색으로 칠해진 곳의 index가 다음노드이다.
📚 인접행렬 탐색 동작 예시
1. 현재 방문 노드: 0
다음노드: 1
현재 간선정보: graph[현재노드] => [0, 1, 1, 0, 0, 0 ]
간선 사용 처리: [0, 0, 1, 0, 0, 0 ]
- 현재 방문 노드: 1
다음노드: 2
현재 간선정보: graph[현재노드] => [0, 0, 1, 1, 0, 0 ]
간선 사용 처리: [0, 0, 0, 1, 0, 0 ]>
- 현재 방문 노드: 2
다음노드: 3
현재 간선정보: graph[현재노드] => [0, 0, 0, 1, 0, 1 ]
간선 사용 처리: [0, 0, 0, 0, 0, 1 ]
- 현재 방문 노드: 3
다음노드: 4
현재 간선정보: graph[현재노드] => [0, 0, 0, 0, 1, 0 ]
간선 사용 처리: [0, 0, 0, 0, 0, 0 ]
- 현재 방문 노드: 4
다음노드: 연결된 정보가 없어 dfs(4)의 함수 호출을 끝내고 dfs(3)의 함수가 돌아가다가 중지된 곳으로 간다. 즉, 위의 코드의 ⭐️ 부분
현재 간선정보: graph[현재노드] => [0, 0, 0, 0, 0, 0]
간선 사용 처리: ❌
- 함수가 실행되는 현재 노드: 2 👉🏻 방문은 이미 했으므로 탐색처리를 하지 않는다.
다음노드: 5
현재 간선정보: graph[현재노드] => [0, 0, 0, 0, 0, 1 ]
간선 사용 처리: [0, 0, 0, 0, 0, 0 ]... 반복 //
사실상 중요한 로직은 주석에 있는 이모지 ⭐️에 다 있다. routes += `${nextNode} 👉🏻 ${dfs(nextNode)}` // ⭐️ 에서 ${nextNode}가 현재 노드 탐색처리이며 ${dfs(nextNode)}부분이 끝까지 탐색을 하는 부분이다.
테스트를 해 보면 잘 나온다.

인접 리스트(Adjacent List)
인접 행렬과 달리 정점과 정점 사이에 간선정보 자체를 배열에 담아서 나타내며 그래프를 나타낼 수 있는 방법 중 하나다.
💡 인접 리스트 특징
- 간선 정보를 배열에 저장한다.
- 각 행에는 간선 정보를 담고있다.
- 각 행의 각 열은 연결된 노드의 정보이다. (Ex; [1, 3] => 1번 노드와 3번 노드 사이에 간선이 존재함)
인접 리스트는 인접 행렬과 정보를 담는 구조만 다르고 나머지 동작원리는 똑같으므로 위의 인접 행렬에서 들었던 예시를 기반으로 설명하겠다.

그래프를 인접 리스트로 나타내면 아래와 같다.
const graph = {
0: [1, 2],
1: [2, 3],
2: [3, 5],
3: [4],
4: [],
5: [],
}구현
위에서 재귀함수와 스택으로 구현할 수 있다고 했는데 stack으로 구현한 것은 없어서 stack도 같이 구현해보겠다.
재귀로 구현
//
const graph = {
0: [1, 2],
1: [2, 3],
2: [3, 5],
3: [4],
4: [],
5: [],
};
function dfs(currentNode) {
let routes = "";
const edgeInfo = graph[currentNode];
for (let idx = 0; idx < edgeInfo.length; idx++) {
if (graph[currentNode][idx] !== false) {
const nextNode = edgeInfo[idx];
graph[currentNode][idx] = false;
routes += `${nextNode} 👉🏻 ${dfs(nextNode)}`;
}
}
return routes;
}
let routes = "0 👉🏻 " + dfs(0);
routes = routes.slice(0, routes.length - 5);
console.log("탐색 순서", routes);<코드확인>

스택으로 구현
⭐️ 간선정보를 의미하는 행에 해당하는 배열에서 pop을 시킨 것은 지금 구현하는 것이 방문한 노드를 제외하여 탐색하는 것이 아닌 간선이 있다면 탐색을 진행하는 것으로 pop을 이용하여 다음 탐색할 노드들을 담음과 동시에 간선정보를 없애 다음 동일한 노드를 탐색시 동일한 간선을 타고 탐색하는 일을 막는다. 스택으로 구현한 것은 이 블로그에 기깔나게 잘 설명이 되어 있어 내가 정리하는 것보다 낳다고 판단하여 이 블로그를 참고하는 것이 더 도움이 될 것 같다.
const graph = {
0: [1, 2],
1: [2, 3],
2: [3, 5],
3: [4],
4: [],
5: [],
};
function dfs(graph) {
let routes = "";
const startNode = 0;
const stack = [startNode];
const visited = Array(Object.keys(graph).length).fill(false);
visited[startNode] = true;
while (stack.length > 0) {
const currentNode = stack.pop();
const edgeInfo = graph[currentNode];
routes += `${currentNode} 👉🏻 `;
while (edgeInfo.length > 0) {
const nextNode = edgeInfo.pop();
stack.push(nextNode);
}
}
return routes;
}
let routes = dfs(graph)
routes = routes.slice(0, routes.length - 5);
console.log(routes);<코드확인>

🔥 마치며
나는 블로그를 처음 공부하면서 바로 쓰지는 않는다. 이유는 내가 다른 사람과 달리 이해가 되지 않은 상태에서 정리한 글들은 내가 봐도 어려우며 남이 봤을 때는 더 어렵기 때문이다. 따라서 처음 공부한 것들은 노션에이나 그냥 손으로 끄적인다.(노션에 있는 거 블로그도 써야되는데 ㅜㅜ) 처음에는 재귀함수조차도 이해하기 너무 버거웠지만 알고리즘 문제를 풀게 되면서 자연스레 어느정도 쓸 수 있어 dfs에 대해서 좀 더 공부하고자 블로그를 쓰게 되었다. 이번에 공부하면서 인접행렬, 인접리스트에 대해서 보다 더 자세히 알게 됐으며 위의 예시들에 대한 코드는 참고한 글이나 블로그가 없어 틀릴 수 있다. 글을 깔끔히 정리하고자 참고한 정도밖에 없으며 예시또한 직접 만들어 확실히 맞다는 것을 보장할 수 없으나 맞는 거 같다^^ 틀리면 알려주세요 ㅜ.ㅜ 블로그 길이 너무 길어져 bfs 파트는 따로 분리하려고 한다.

