🍀BFS(Breadth-First Search)
이전 블로그(DFS)에 이어서 이번에는 BFS에 대해서 알아보자. breadth는 사전의미로 폭이란 의미를 갖는다. 영어에 맞게 번역을 하면 너비 우선 탐색이다. 즉, 가장 가까운 정점 또는 노드부터 탐색하여 말단에서 끝나는 탐색 알고리즘이다. 이번 시간에도 DFS에서 했던 것과 마찬가지로 tree(트리), adjacent list(인접 리스트), adjacent matrix(인접 행렬)에서의 동작과 구현을 기반으로 공부할 생각이다. BFS는 Queue를 이용하여 구현할 수 있다. 아래는 bfs가 탐색하는 과정을 보여준다.
애니메이션에서 볼 수 있듯이 같은 sibling node들을 먼저 탐색한다.
본격적으로 들어가기 앞서 bfs 특징을 한 번 정리하고 들어가보자.
💡 특징
- 현재 노드에서 가장 가까운 노드부터 탐색한다.
- queue를 이용하여 구현한다.
- dfs보다 빠르다고는 하는데 상황에 따라 다르긴 하다.
- 최단 거리, 미로 찾기, 네트워크 라우팅등에 적합한 탐색 알고리즘이다.
Tree
Tree 자료구조에서의 bfs 탐색 과정을 살펴보자. 예시는 랜덤한 값을 가진 tree를 탐색하는 과정을 출력하는 것으로 해 보겠다. 만약에 아래와 같은 tree가 있다고 가정하자.
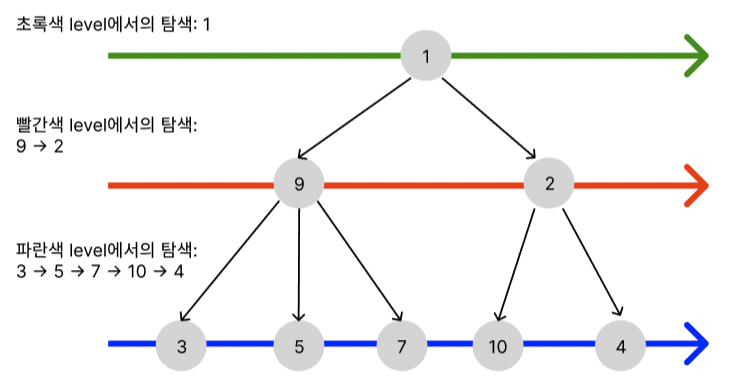
BFS는 너비 우선 탐색이기 때문에 쉽게 말하자면 같은 층 즉, 형제 노드들을 먼저 탐색한다. 따라서 좌에서 우로 초록색 층, 빨간색 층, 파란색 층을 순서대로 탐색을 진행하면 1 -> 9 -> 2 -> 3 -> 5 -> 7 -> 10 -> 4가 탐색 순서가 된다.
구현
BFS는 Queue를 이용해서 구현할 수 있는데 트리가 크지 않으니 그냥 javascript Array API인 shift, unshift method로 구현하겠다. shift와 unshift 동작을 수행할 때 O(1)의 시간 복잡도를 가져야 하는데 이는 LinkedList를 이용하여 Queue를 구현해야 한다. 이와 관련된 글은 여기에 정리해두었다.
먼저 트리를 만들기 위한 코드이다.
트리 구현
class Tree {
constructor(value) {
this.value = value;
this.childNodes = [];
}
insert(childNode) {
this.childNodes.push(childNode);
return this;
}
}
const rootTree = new Tree(1);
const tree9 = new Tree(9);
const tree2 = new Tree(2);
rootTree.insert(tree9);
rootTree.insert(tree2);
tree9.insert(new Tree(3));
tree9.insert(new Tree(5));
tree9.insert(new Tree(7));
tree2.insert(new Tree(10));
tree2.insert(new Tree(4));
console.log(rootTree);
BFS 구현
function bfs(rootTree) {
const queue = [rootTree];
const routes = [];
while (queue.length > 0) {
const currentNode = queue.shift();
routes.push(currentNode.value);
for (const childNode of currentNode.childNodes){
queue.push(childNode)
}
}
return routes;
}
const routes = bfs(rootTree);
console.log(routes.join(" 👉🏻 "));
위에서 언급한 탐색순서와 일치함을 볼 수 있다.
인접 행렬(Adjacent Matrix)
인접행렬의 예시또한 DFS에서 했던 예시를 가지고 와서 들겠다.
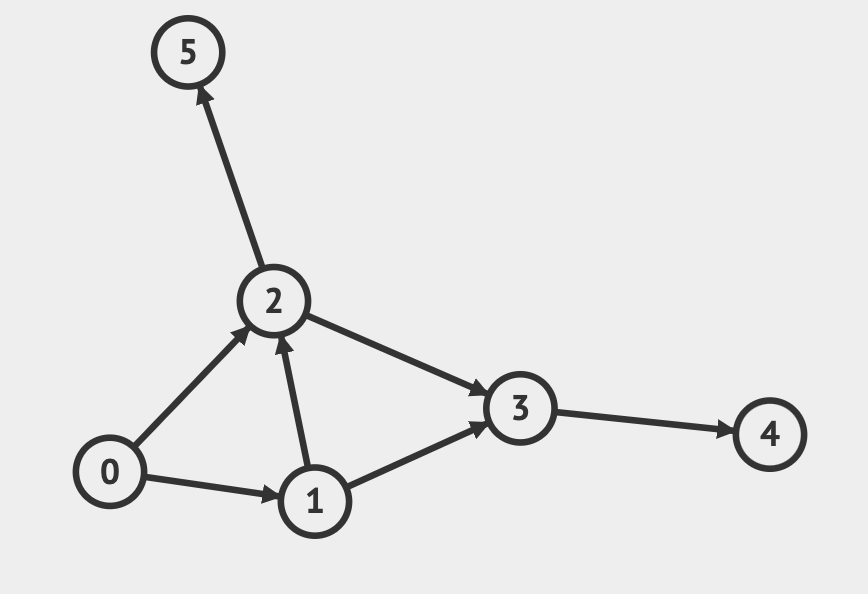
인접 행렬 간선정보
const graph = [
[0, 1, 1, 0, 0, 0 ],
[0, 0, 1, 1, 0, 0 ],
[0, 0, 0, 1, 0, 1 ],
[0, 0, 0, 0, 1, 0 ],
[0, 0, 0, 0, 0, 0 ],
[0, 0, 0, 0, 0, 0 ]
]이 그래프의 탐색 순서를 예측해보자. BFS는 가장 가까운 노드부터 탐색한다고 했으며, queue를 이용하여 구현할 수 있다고 했다. queue에는 어떤 정보가 담길까? queue는 FIFO(First-In-First-Out) 특징을 가지므로 다음 탐색할 노드에 대한 정보를 담고 있다. 따라서, 현재 탐색 중인 노드와 가장 가까운 노드가 가장 먼저 queue에 들어갔다가 가장 먼저 나옴으로써 탐색을 진행하기 때문에 BFS동작원리를 따를 수 있는 것이다.
값이 0인 node부터 탐색한다고 가정하면 아래와 같은 탐색 순서를 예상할 수 있다.
💡 graph정보에 대한 bfs탐색순서 예측
1.0번 노드시작
2. 0번 노드와 가까운1번, 2번 노드 탐색
3. 1번 노드와 가까운3번 노드 탐색
4. 2번 노드와 가까운5번 노드 탐색
5. 3번 노드와 가까운4번 노드 탐색
6. 4, 5번 노드와 가까운 노드는 없으므로 탐색하지 못 한다.따라서, 탐색 순서는
0 -> 1 -> 2 -> 3 -> 5 -> 4가 된다.
그림을 통해서 명확하게 한 번 알아보자!!!!(현재 탐색 중인 노드는 주황색, 방문 처리 노드는 빨간색이다.)
인접 행렬에서의 bfs 탐색 과정
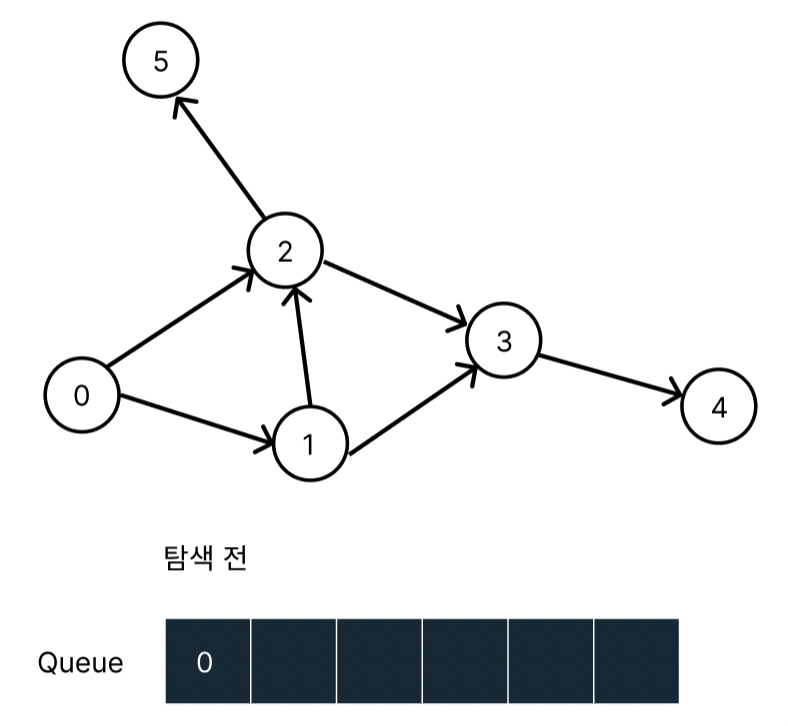
탐색 전 queue에는 시작 지점(값이 0인 노드)에 대한 정보를 넣어준다. 이유는 queue에서 dequeue가 되면서 노드를 방문하기 때문이다.
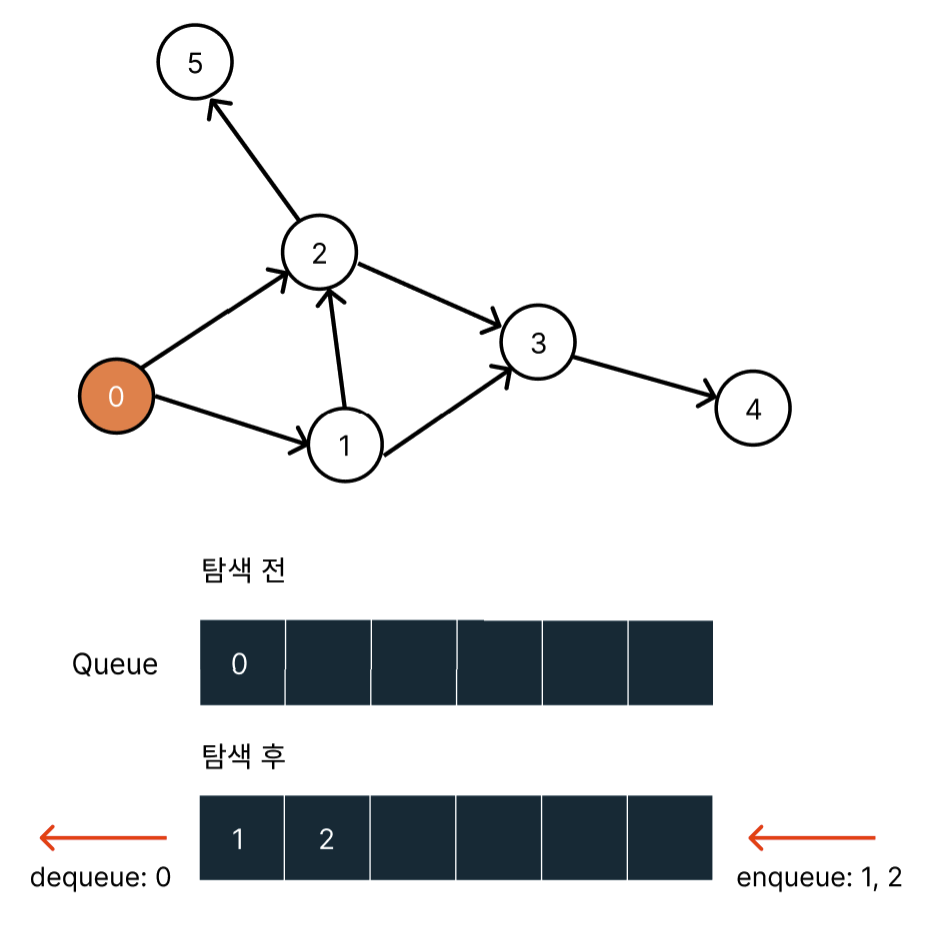
0번 노드를 탐색했을 때 방문처리를 하고 0번 노드와 가까운 1, 2 노드를 queue에 밀어넣는다.
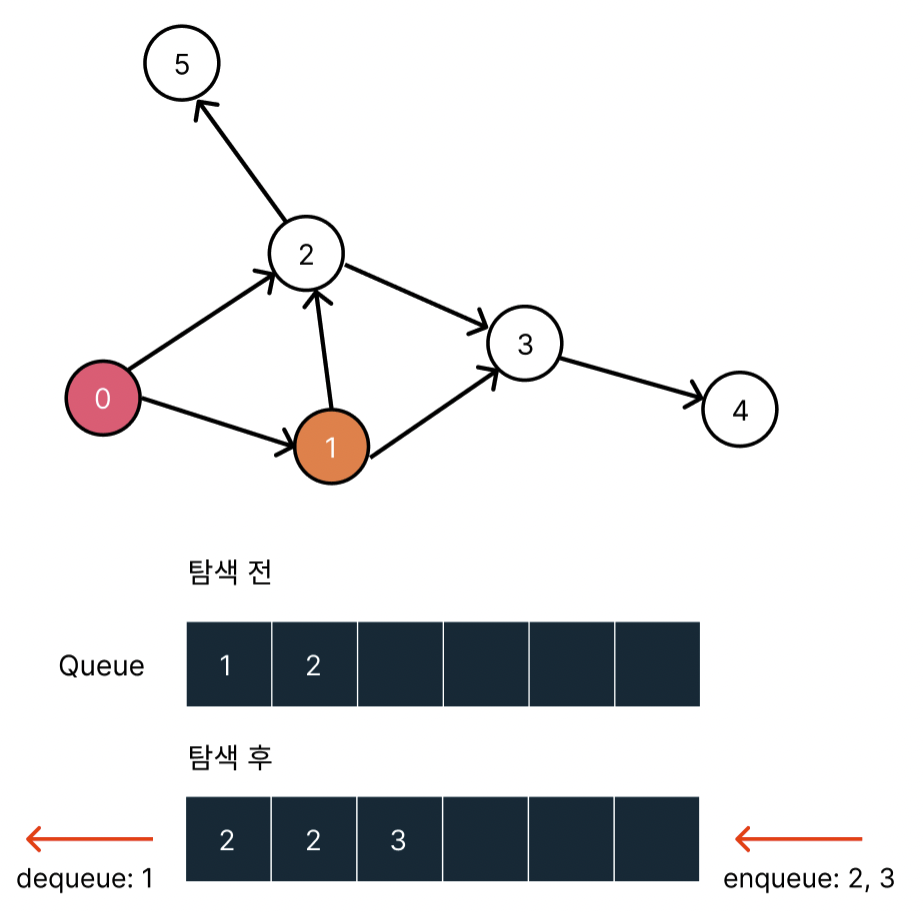
1번 노드를 탐색하고 1번 노드와 가까운 2, 3 노드를 queue에 밀어넣는다.
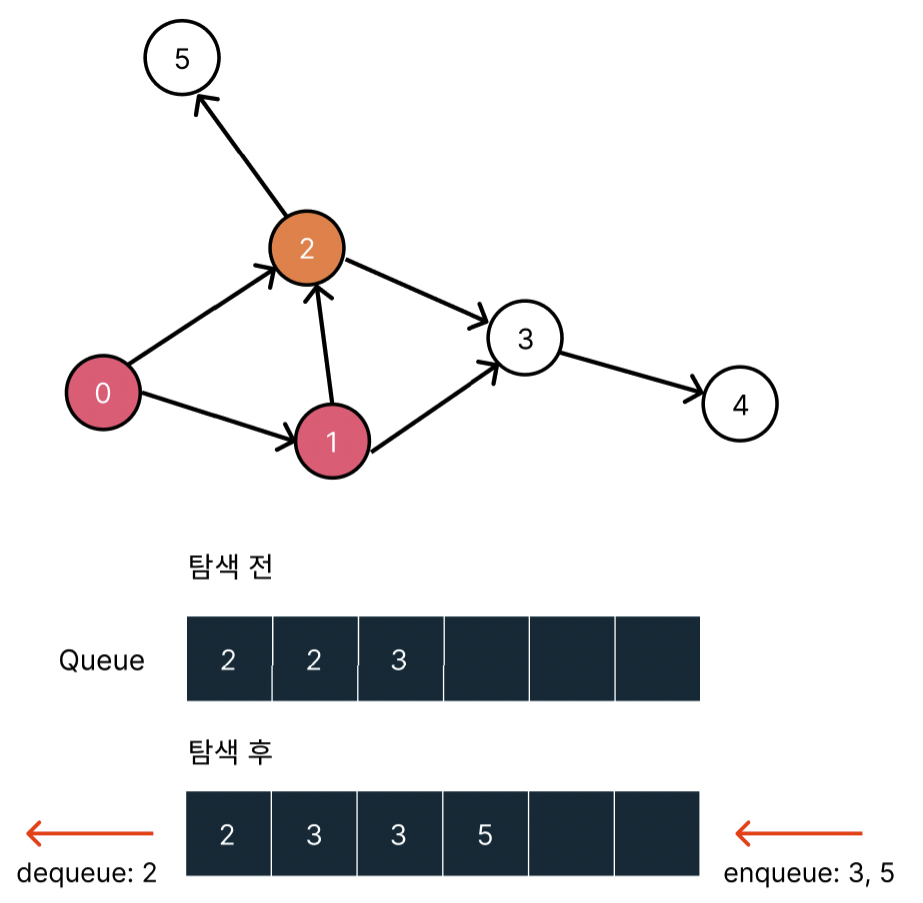
2번 노드를 탐색하고 2번 노드와 가까운 3, 5 노드를 queue에 밀어넣는다.
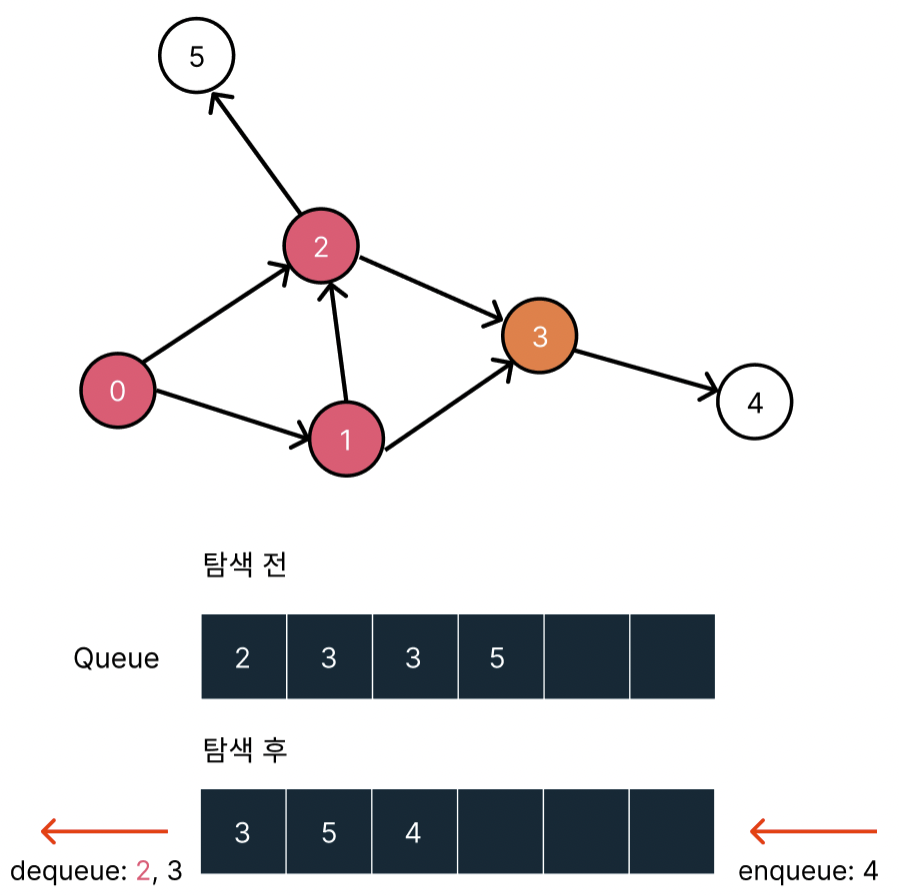
2번 노드는 이미 방문했으므로 방문하지 않은 3번 노드까지 dequeue하고 방문처리한다. 그리고 3번 노드와 가까운 4 노드를 밀어넣는다.
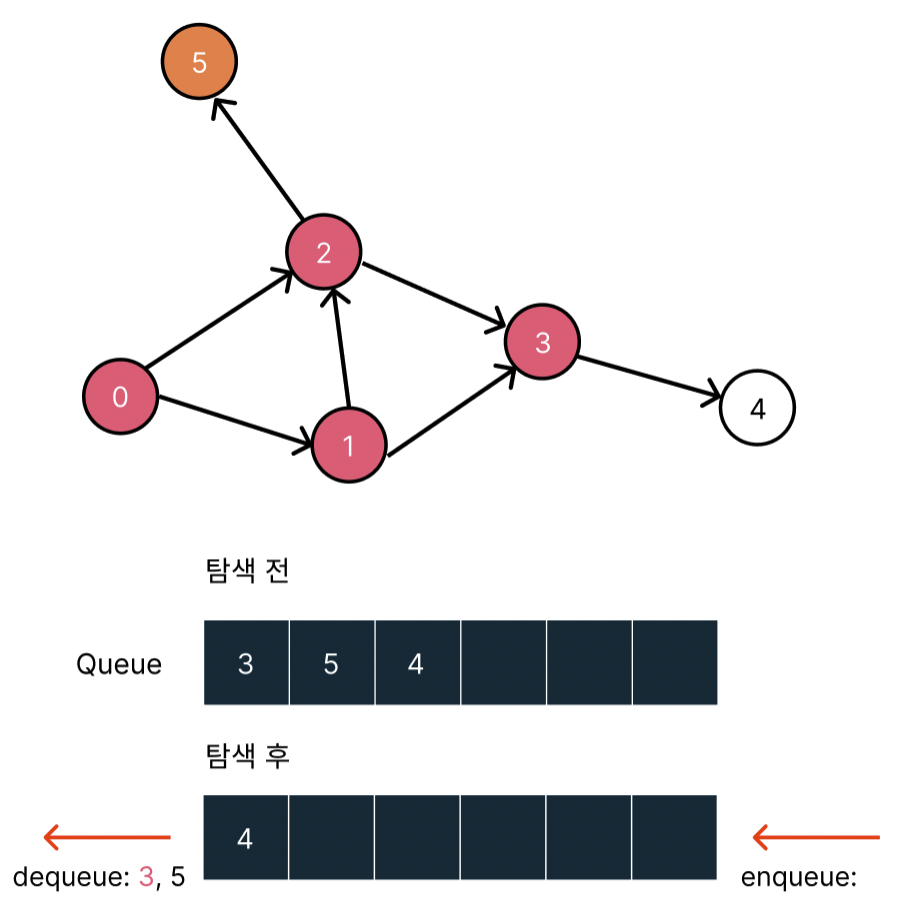
3번 노드는 이미 방문했으므로 방문하지 않은 5번 노드까지 dequeue하고 방문처리한다. 그리고 5번 노드와 가까운 노드가 존재하지 않으므로 다음 탐색 노드를 밀어넣지 못 한다.
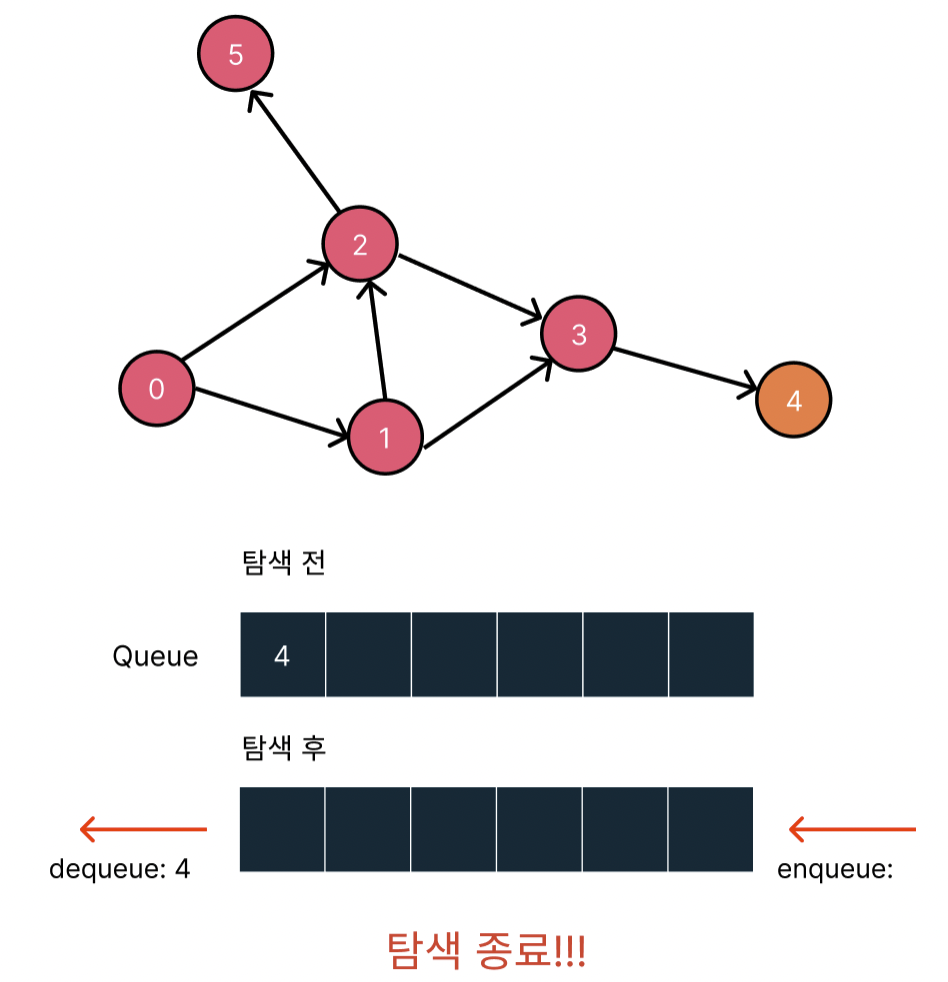
마지막 4번 노드를 탐색하고 4번 노드와 가까운 노드가 존재하지 않으므로 다음 탐색 노드를 밀어넣지 못 하고 다음 루프에서 queue가 비어있어 탐색이 종료된다.
처음에는 이해가 잘 가지 않을 수 있으나, 천천히 생각하면 충분히 이해할 수 있다. 이제 탐색 과정이 어떻게 진행되는지 알았으므로 queue를 이용하여 bfs 탐색을 구현해보자
구현
function bfs(start, graph) {
const queue = [start];
const routes = [start];
const visited = Array(graph.length).fill(false);
visited[start] = true;
while (queue.length > 0) {
const currentNode = queue.shift(); // 1️⃣ 현재 방문노드
for (let nextNode = 0; nextNode < graph[currentNode].length; nextNode++) {
const canGo = graph[currentNode][nextNode];
if (!visited[nextNode] && canGo) { // 2️⃣ 방문(탐색)하지 않았으며 간선이 있을 때 다음 탐색을 위해 가까운 노드 정보들을 넣어준다.
routes.push(nextNode);
visited[nextNode] = true;
queue.push(nextNode);
}
}
}
return routes;
}
const graph = [
[0, 1, 1, 0, 0, 0],
[0, 0, 1, 1, 0, 0],
[0, 0, 0, 1, 0, 1],
[0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
];
const routes = bfs(0, graph);
console.log(routes.join(" 👉🏻 "));가장 중요한 로직은 코드 부분의 1️⃣과 2️⃣이다.
콘솔을 찍어보면 이 또한 잘 나온다.

bfs를 인접 행렬로 구현하게 되면 모든 노드를 한 번씩 방문(while문)하며 한 번 방문할 때 마다 노드와 연결된 간선정보(for 구문 => 행에 해당하는 리스트)를 돌게 되므로 O(N^2) 시간 복잡도를 가지게 된다.
인접 리스트(Adjacent List)

위의 graph를 인접리스트로 바꾸면 아래와 같다.
인접 리스트 간선정보
const graph = {
0: [1, 2],
1: [2, 3],
2: [3, 5],
3: [4],
4: [],
5: [],
}인접 리스트 구현은 인접 행렬 구현과 다른 점은 그저 graph 정보를 담는 형식이 다르다는 것이고 나머지 로직은 같다. 이번에는 동작과정을 도식화하지는 않겠다.
구현
const graph = {
0: [1, 2],
1: [2, 3],
2: [3, 5],
3: [4],
4: [],
5: [],
};
function bfs(start, graph) {
const queue = [start];
const routes = [start];
const visited = Array(graph.length).fill(false);
visited[start] = true;
while (queue.length > 0) {
const currentNode = queue.shift();
for (const nextNode of graph[currentNode]) {
if (!visited[nextNode]) {
routes.push(nextNode);
visited[nextNode] = true;
queue.push(nextNode);
}
}
}
return routes;
}
const routes = bfs(0, graph);
console.log(routes.join(" 👉🏻 "));인접 리스트에 들어있는 노드들은 이미 간선이 존재하는 노드들 이므로 인접 리스트에서 구현한 canGo라는 조건이 필요가 없다. 따라서 방문처리만 해주면 깔끔하게 돌아간다.
bfs를 인접 리스트로 구현하게 되면 O(N + E) 시간 복잡도를 가지게 된다. 이 때 N은 Node수, E는 간선(Edge)의 수이다. 인접 행렬로 구현 한 것과 달리 각 노드를 방문할 때 모든 노드와의 연결정보를 확인하지 않게 되므로 간선의 수 만큼만 루프를 돌게 되기 때문이다.
구현도 했고 dfs, bfs가 무엇인지 알았으니 인접행렬과 인접리스트의 차이점을 정리하면서 마무리 해보자.
🔎 인접행렬 VS 인접 리스트
인접행렬(Adjacent Matrix)
- 시간 복잡도: 인접 행렬은 노드를 N이라 할 때 N 개수만큼 N번 dfs 함수를 호출하므로 N * N인
O(N^2).- 장점: 서로 간의 연결정보를 파악하기 쉬움.
- 단점:
- N * N만큼 메모리를 차지하지 하므로 인접 리스트에 비해 공간을 더 많이 차지함.
- 인접 리스트에 비해 시간이 좀 더 느리다.- 적합한 상황: 간선의 정보가 많은 상황에 적합 (간선의 수가 노드의 수와 비슷할 때)
인접리스트(Adjacent List)
- 시간 복잡도: 노드 N 간선 E라고 표현할 때 O(N + E) 시간 복잡도를 가진다.
- 장점:
- 인접행렬과 달리 메모리를 덜 차지한다.
- 인접행렬에 비해 좀 더 빠르다.- 단점:
- 인접행렬은 노드간의 간선정보를 파악하는데O(1)의 시간이 걸리지만, 인접리스트는 간선정보를 다 찾아야 하므로O(N)의 시간이 소요된다.- 적합한 상황: 간선의 개수가 노드의 개수보다 적을 때(Ex; 희소 그래프) 상황에 적합하다
🔥 마치며
dfs와 bfs를 이용하여 알고리즘 문제를 조금 풀어봤지만 천재와 달리 풀면서 이해가 가기 시작한 케이스이다. 그래도 재귀, dfs, bfs를 처음 접할 때는 넘지 못할 산처럼 느껴졌지만 이제 슬슬 정복해가는 느낌이다. 난 비록 이해하는데 시간이 느리지만 이후에 응용하는 것은 남들보다 빠르다는 자신이 있다. dfs, bfs를 블로그를 쓰기 위해 한 번 더 정리하고 예제를 만들어보고 스스로 검증하는 과정에서 이 녀석들을 더 잘 이해하는 계기가 되었다. 시간이 걸려도 꾸준히 천천히라도 하다 보면 언젠간 골칫거리인 문제들을 타파할 수 있다는 강한 자신감을 얻어가면서 블로그를 마무리한다.


