🍀 HEAP(힙)
힙은 최대값 또는 최소값을 찾기 위해 고안된 자료구조이다. 어떤 배열에서 최대값을 찾는다고 가정하고 코드를 구현하게되면 통상적으로 O(N)의 시간 복잡도를 가지게 된다. 하지만, 힙을 이용하면 O(logN)만에 최대값 또는 최소값을 찾을 수 있다. 이 때, 로그함수의 밑은 2이다.(새롭게 안 사실!!)
추가적으로 힙의 사전적으로 차곡차곡 쌓여있는 더미를 의미한다. 돈 더미, 산 더미, 모래 더미등을 연상케한다. 아래 사진을 보면 tree구조와 비슷하다!!

특징
힙을 어느 상황에서 쓰면 좋은지 알아봤으니 어떤 특징을 가지는지 살펴보자.
🔎 힙 특징
- sibling node(형제 노드)들 간에
순서나 관계가 존재하지 않는다.- max heap(최대 힙): 부모는 자식노드보다
항상 큰 값을 가진다.
min heap(최소 힙): 부모는 자식노드보다항상 작은 값을 가진다.- heap은
완전 이진 트리(complete binary tree)이다.- parent 위치: Math.floor((childIndex - 1) / 2)
- child 위치: left 👉🏻 2 x parentIndex + 1
right 👉🏻 2 x parentIndex + 2
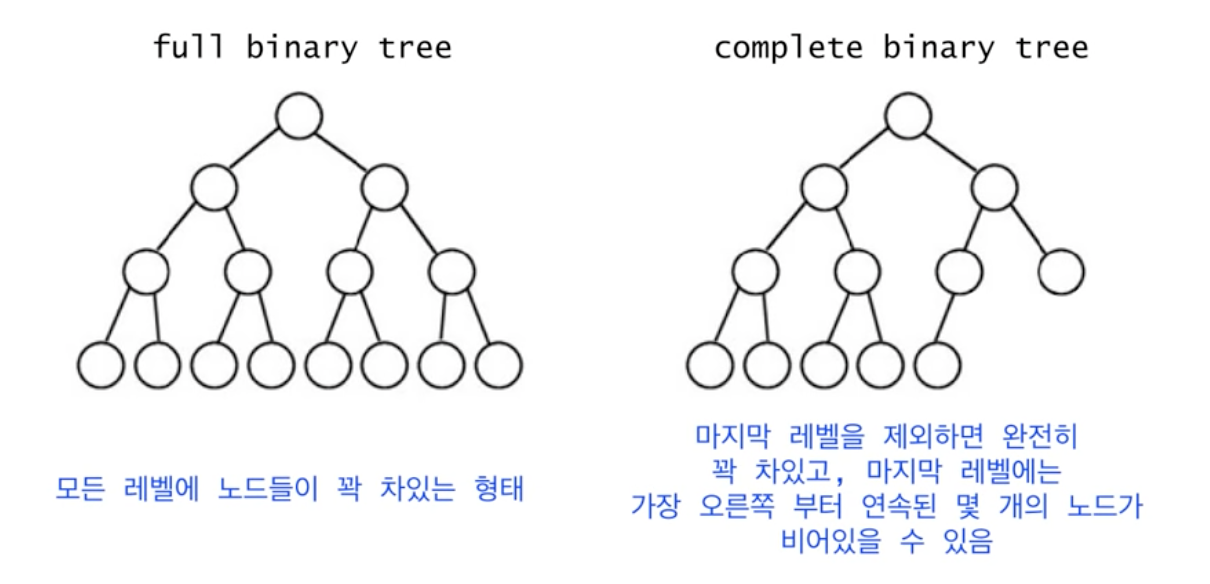
이 때 완전 이진 트리(complete binary tree)와 정(full binary tree)와 다르다.
자식, 부모위치 가져오기
parent, child위치가 왜 저런 수식을 갖나 되나. 힙을 구현할 때 여러방식으로 구현하는데 나는 배열을 이용하여 구현하겠다.
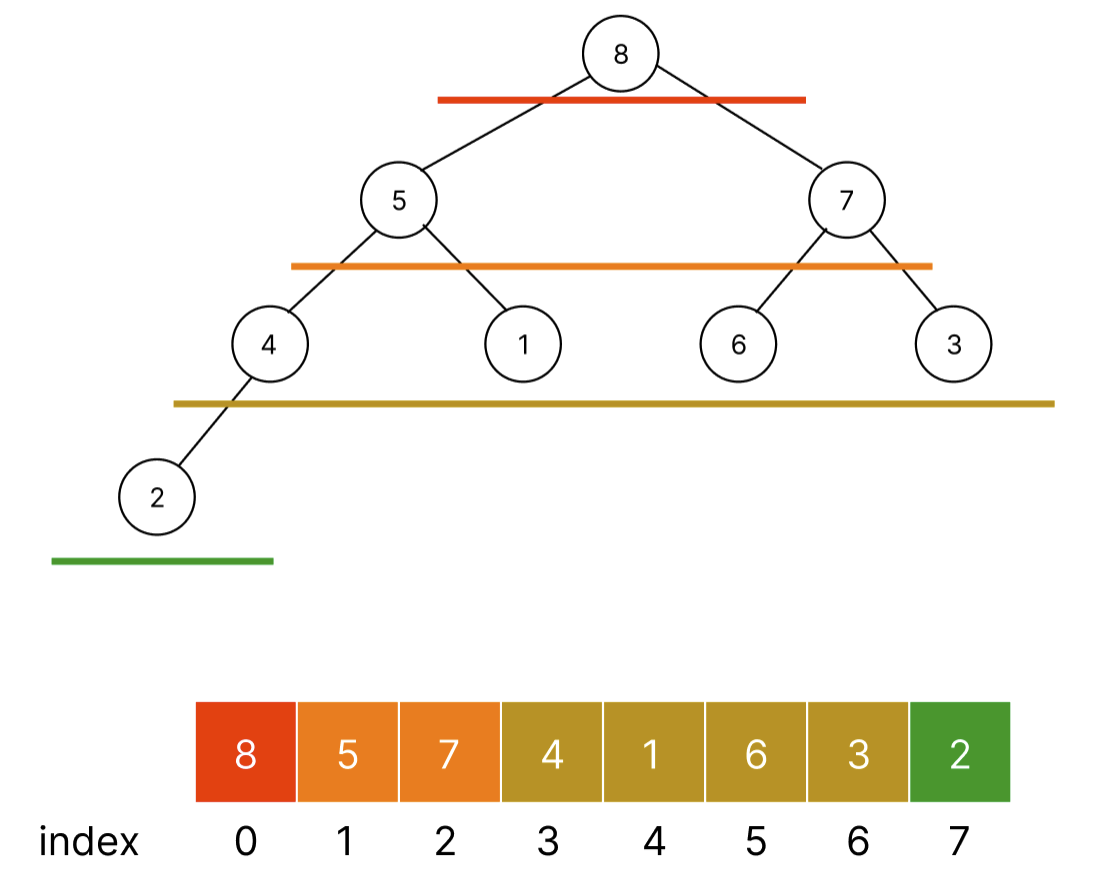
각 level이 낮음 -> 높음 순서대로 배열 앞에 놓인다. 따라서 rootNode인 8이 index = 0에 존재하게 되는 것이고 leaf node가 배열의 끝 부분에 존재하게 된다.
parent node 위치(Math.floor((childIndex - 1) / 2))와 child node의 위치 (2 * parentIndex + 1, 2 * parentIndex + 2)가 될까????
만약에 값이 7 index = 2인 node에서 leftChild와 rightChild의 위치를 배열에서 구한다고 해 보자.
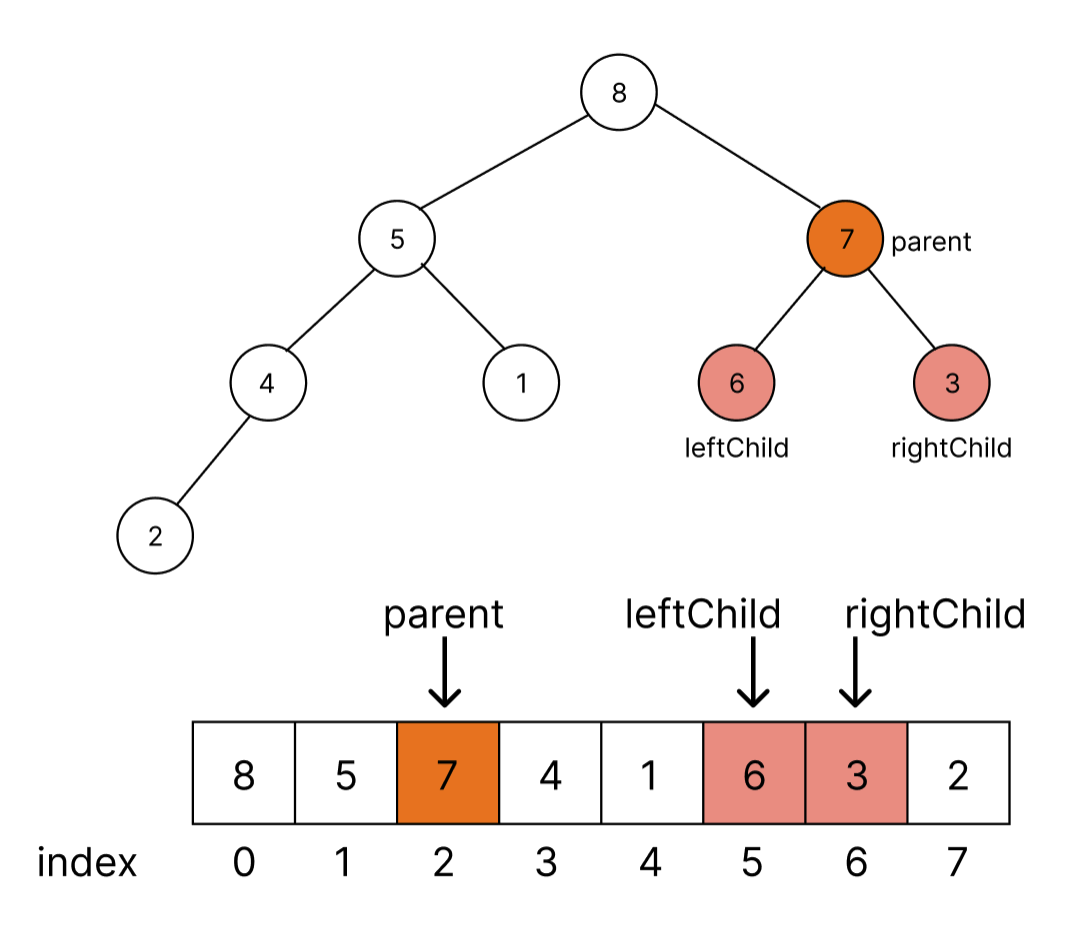
heap가 완전 이진 트리 구조를 가지고 있기 때문에 depth가 높아짐에 따라 자식 노드의 개수는제곱으로 증가함으로 2와 연관이 있음을 알 수 있다. 일단, leftChild, rightChild 위치를 구해보자.
leftChild = 2 x parentIndex + 1 = 2 x 2 + 1 =
5
rightChild = 2 x parentIndex + 2 = 2 x 2 + 2 =6
따라서, 부모위치가 parentIndex일 때 왼쪽, 오른쪽 자식은 각각 2 x parentIndex + 1, 2 x parentIndex + 2수식을 통해서 알아낼 수 있다.
반대로 child위치로부터 parent위치를 알 수도 있다. 이번에는 값이 1, index = 4인 곳에서 부모 위치를 알아보자.
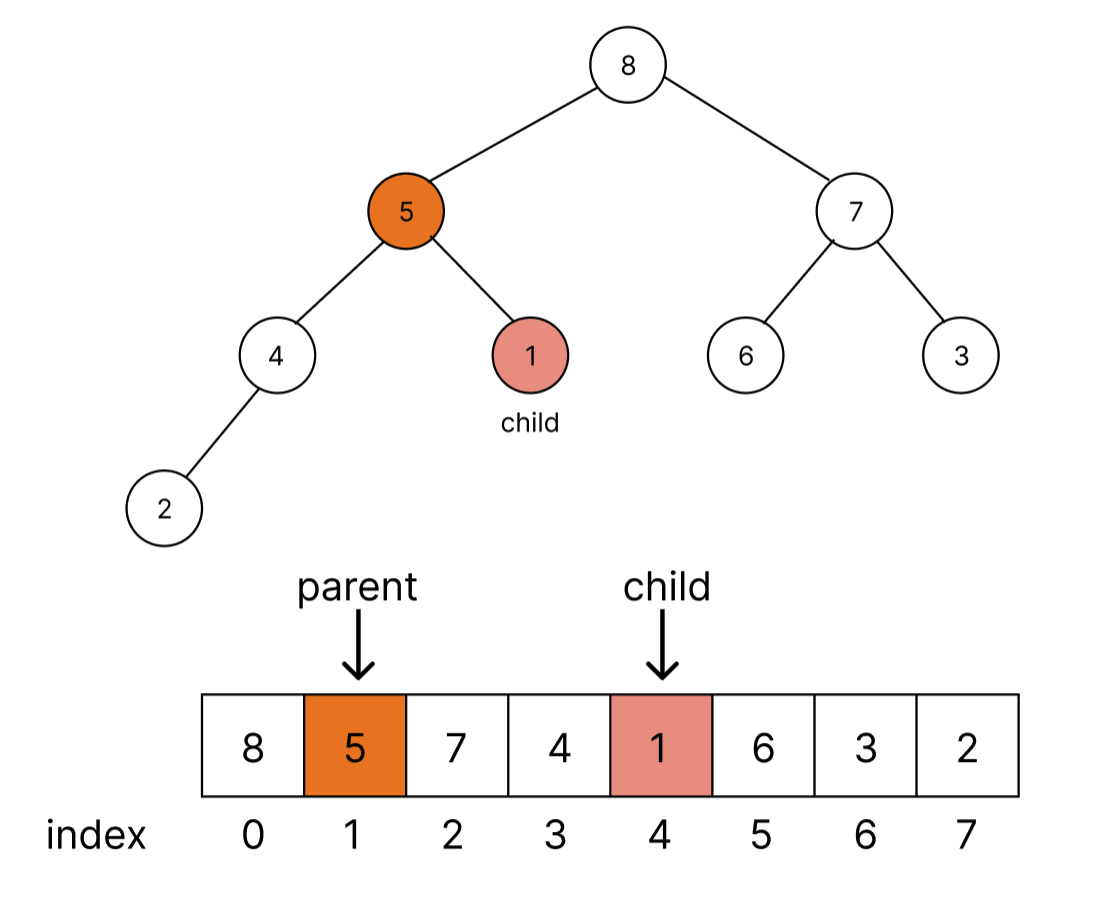
parent = Math.floor((childIndex - 1) / 2) = Math.floor((4 - 1) / 2) = Math.floor(1.5) =
1
값이 4, index = 3에서는 어떨까?
parent = Math.floor((childIndex - 1) / 2) = Math.floor((3 - 1) / 2) = Math.floor(1) =
1
따라서, 자식위치가 childIndex일 때 부모는 Math.floor((childIndex - 1) / 2) 수식을 통해 알 수 있다.
🛠️ 구현
힙은 대표적으로 데이터를 추가하는 push, 최대 또는 최소값을 가져오는 pop 그리고 마지막으로 정렬인 heapify 순으로 구현하겠다. method명은 python의 heapq를 따라했다. 최소 힙은 최대 힙과 반대로 하면 되므로 최대 힙을 기준으로 구현했다. 아래 구현은 [5, 4, 7, 9, 8, 1]데이터를 기반으로 한다.
1️⃣ push(O(logN))
heap을 배열로 구현했기 때문에 값을 push하게 되면 배열의 맨 뒤에 값이 들어오게 된다. 들어온 값은 leaf node에 위치하며 부모들과 대소 관계를 비교하여 적절한 위치에 놓이게 만들어야 한다.
먼저 예시 데이터를 완전 이진 트리 형태로 보자.(아래 그림은 정렬이 되어 있는 상태)
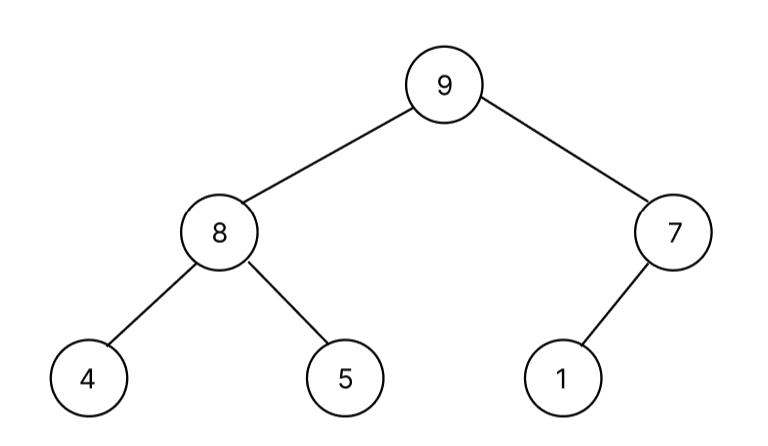
이러한 데이터에 10이란 데이터가 들어온다고 가정하자. 그러면 기존 heap은 [9, 8, 7, 4, 5, 1]에서 [9, 8, 7, 4, 5, 1, 10]처럼 배열 끝에 들어온다.
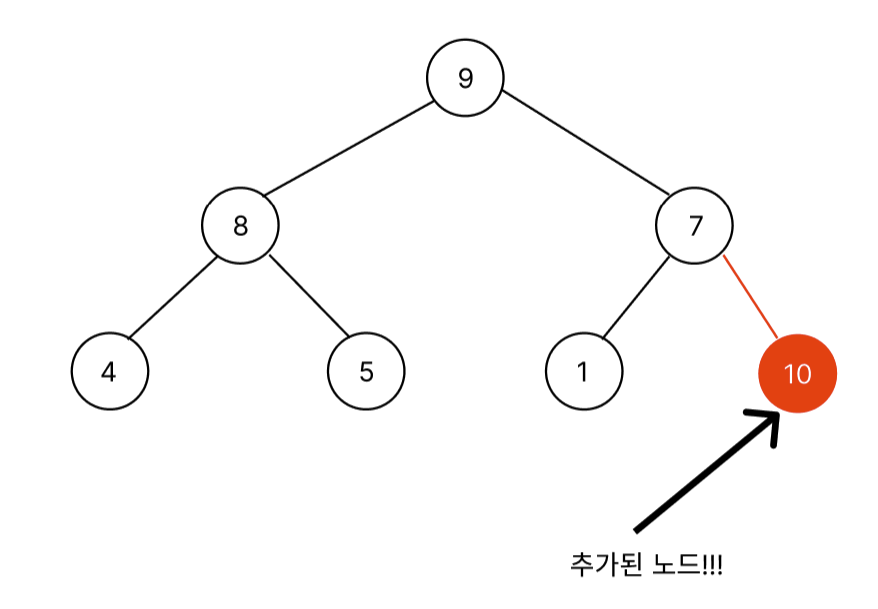
육안으로 확인해봐도 10이란 값이 가장 큰데 가장 밑에 존재하고 있다. 따라서, root로 올라가면서 추가된 노드의 값이 부모의 값보다 작을 때까지 대소관계를 비교한다. 이렇게 부모와 대소관계를 비교하면서 올라가는 과정을 bubbleUp이라는 함수로 구현하겠다. siftDown이라고도 하며 사실상 이름은 자기 자신이 짓기 마련이다. 나는 colt steele강사의 강좌를 참고하였으니 bubbleUp으로 명명했다.
데이터가 추가된 후 bubbleUp되는 과정을 살펴보자.
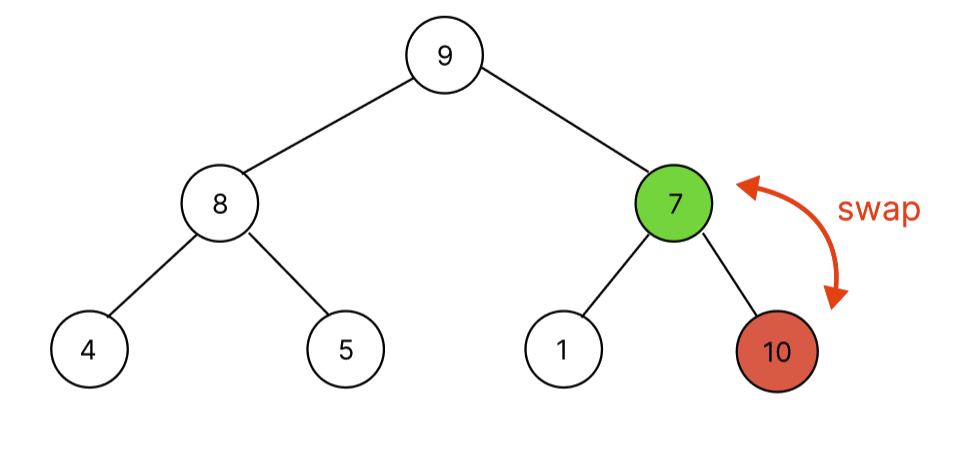
추가된 데이터 10은 자식노드로서 부모노드의 값인 7보다 크다. 따라서 부모와 자식과 swap한다.
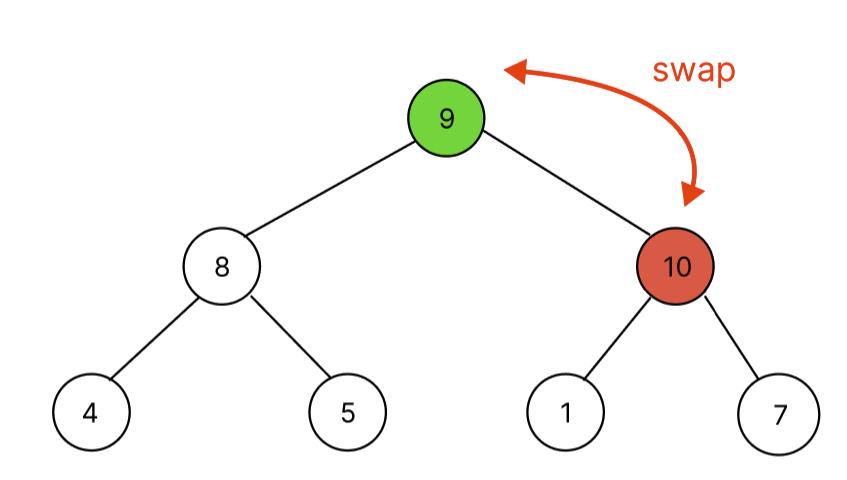
마찬가지로 자식 노드 10은 부모노드 9보다 크므로 swap한다.
이후 root노드까지 도달했으니 push함수 호출을 끝낸다. 따라서, 10이 추가된 heap은 [10, 8, 9, 4, 5, 1, 7]이 된다.
이제 bubbleUp함수를 만들어보자!!!
class Heap {
constructor(heap = []) {
this.heap = heap;
this.heapify();
}
push(value) {
this.heap.push(value);
this.bubbleUp();
}
bubbleUp() {
let pos = this.heap.length - 1;
const pushedValue = this.heap[pos];
while (pos > 0) {
const parentPos = (pos - 1) >> 1;
const parentValue = this.heap[parentPos];
if (pushedValue > parentValue) {
this.heap[pos] = parentValue;
pos = parentPos;
continue;
}
break;
}
this.heap[pos] = pushedValue;
}
}
const arr = [9, 8, 7, 4, 5, 1];
const heap = new Heap(arr);
heap.push(10);
console.log(heap.heap); // [10, 8, 9, 4, 5, 1, 7]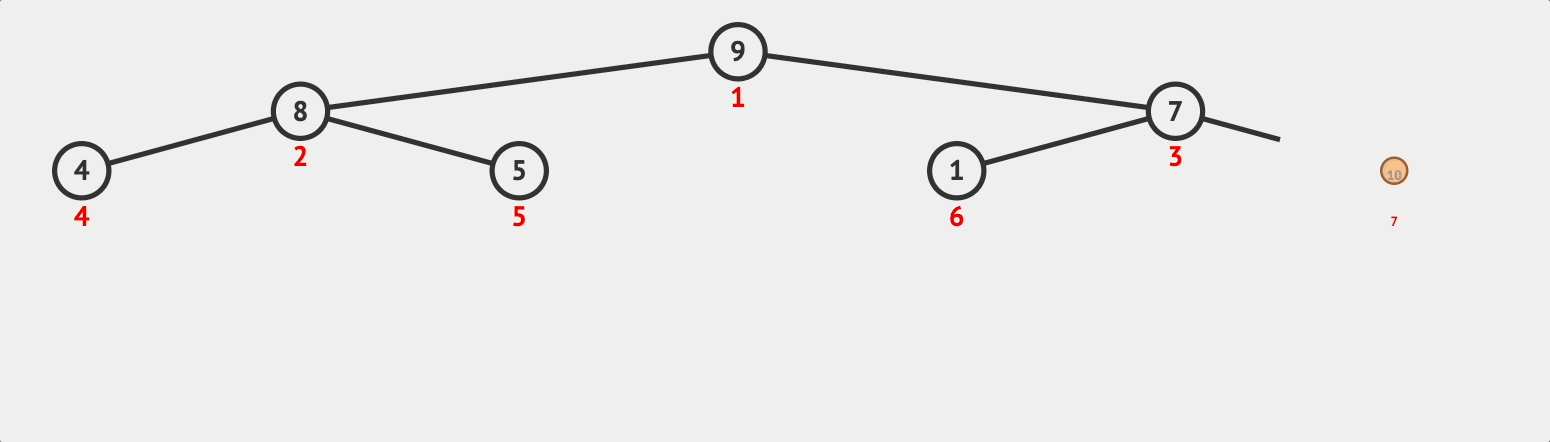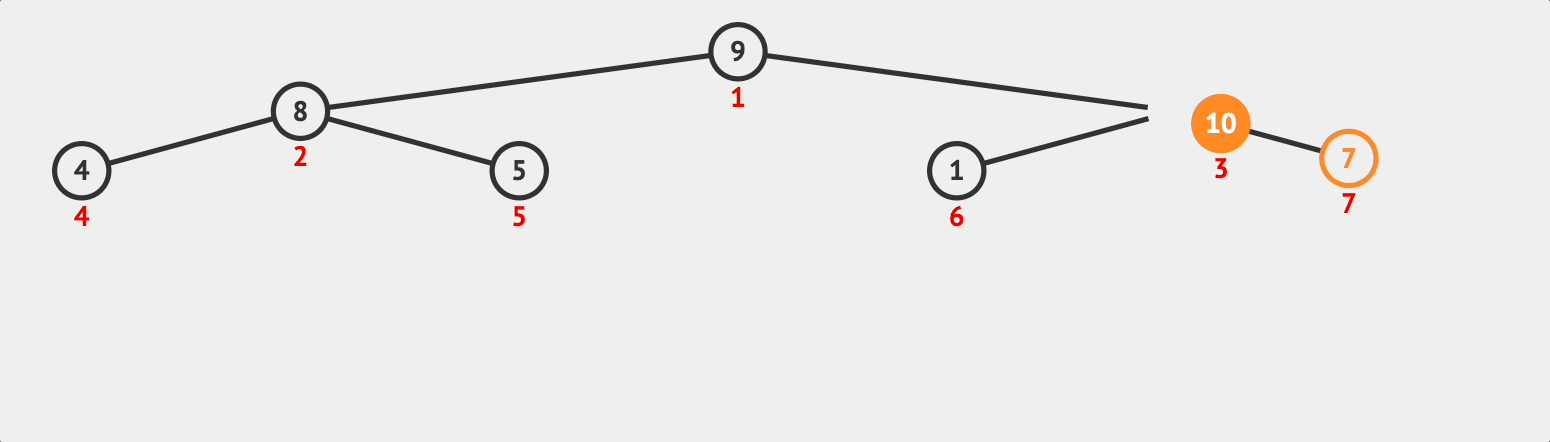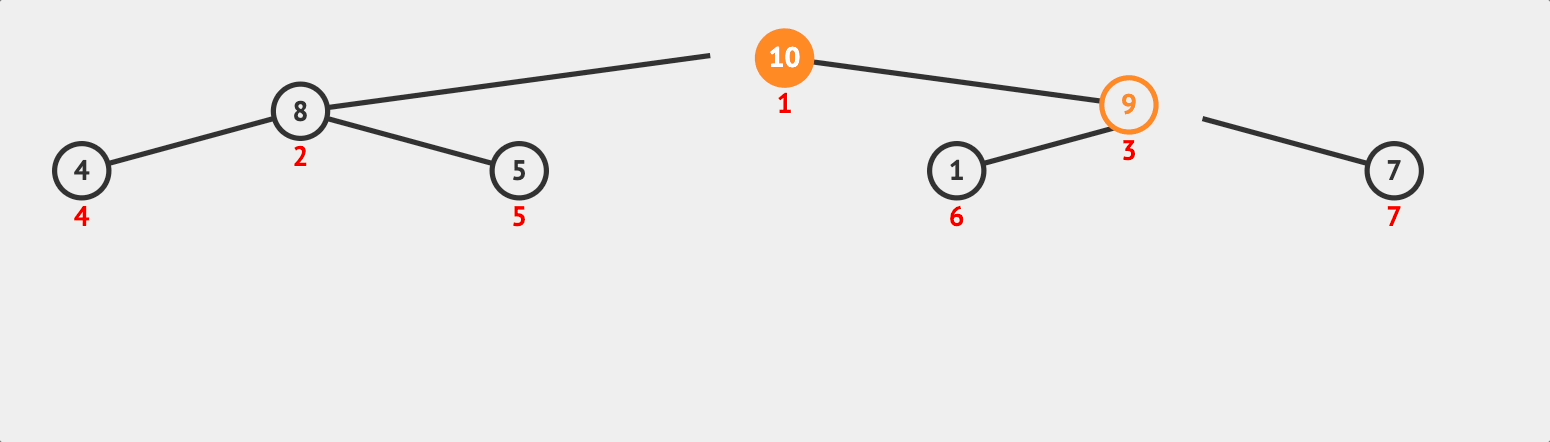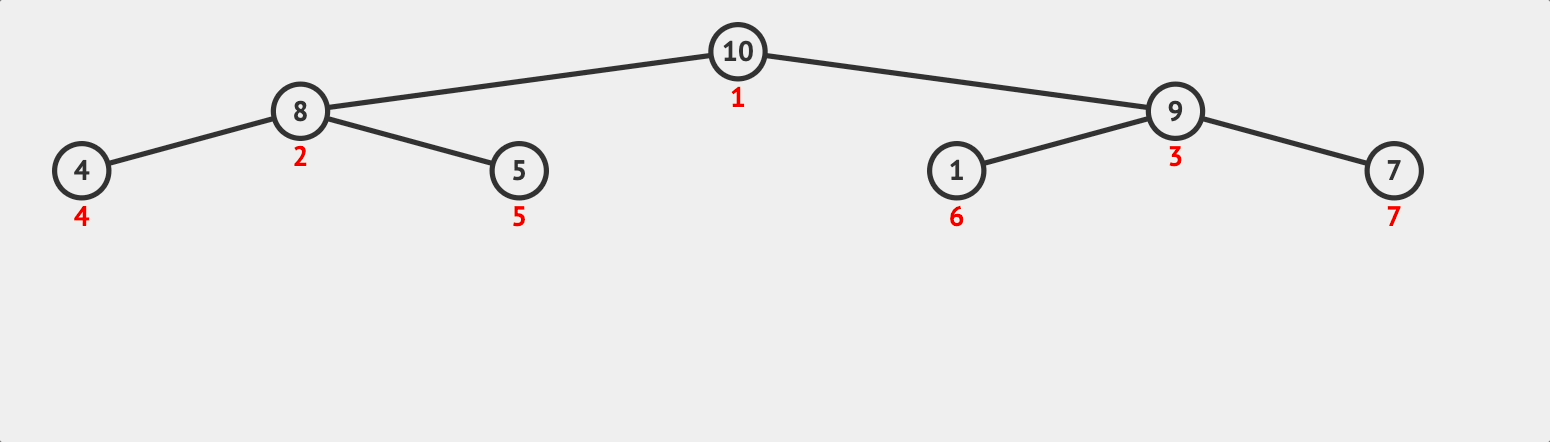
위에 대한 동작과정 애니메이션이다. visualalgo에서 원하는 값을 추가하고 애니메이션으로 확인할 수 있다!
2️⃣ pop(O(logN))
최대 힙에서 pop을 하면 최대값이 pop되며 최소 힙에서는 최소값을 pop한다. heap에서의 pop은 항상 root node의 값을 pop한다. 하지만, root node를 제거하면 배열의 앞에서 빼는 것으로 배열의 shift메서드를 사용하는 것과 다름이 없다. shift메서드를 이용해서 pop을 시킨다면 heap에서 pop할 때 시간 복잡도는 O(NlogN)을 갖게 될 것이다. 하지만, 배열의 root node(index = 0)와 배열의 마지막 요소와 swap 후 배열의 pop 메서드를 사용하면 O(1)로 heap에서는 O(logN) 시간 복잡도를 가지게 할 수 있다. 아래 pop하는 과정을 그림을 통해서 살펴보자.
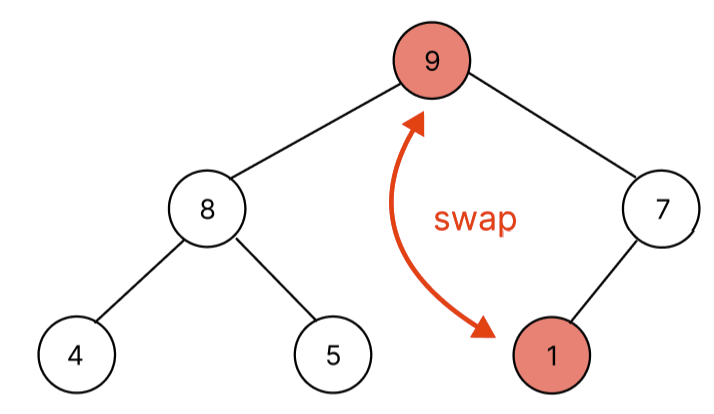
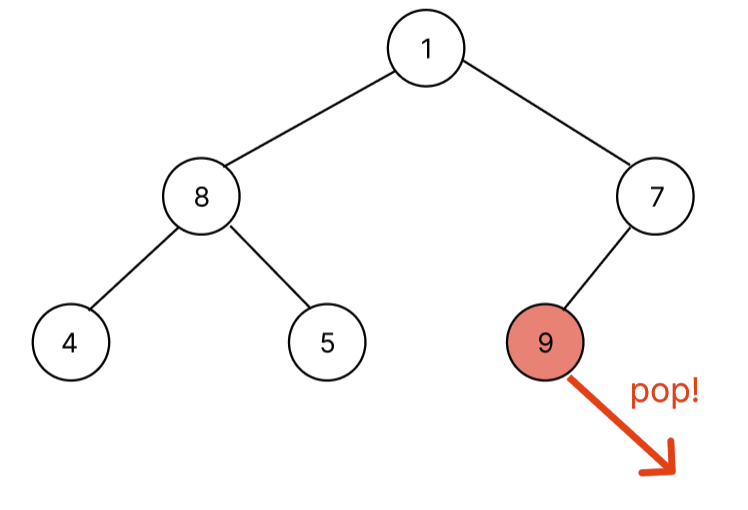
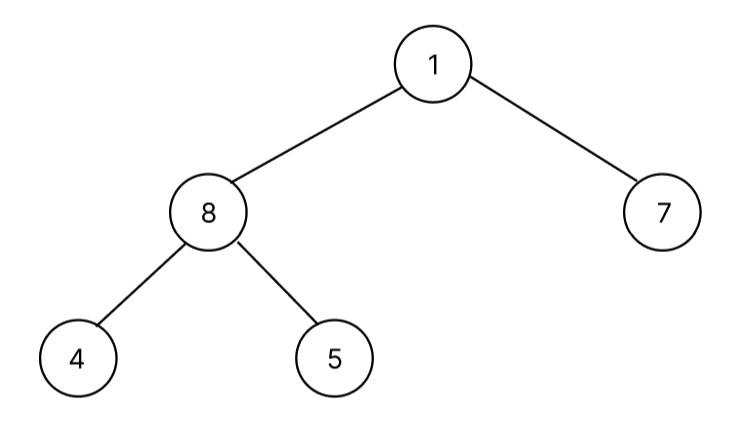
자세히 보면 이상한 점이 존재한다. pop을 하기위해 swap을 하니 가장 작은 노드가 root node에 위치한다는 것이다. 따라서, 루트노드부터 마지막 노드까지 부모 자식과 대소관계를 비교해야 한다. 위에서 아래로 내려가면서 비교를 해야하는데 bubbleDown 함수로 구현했다.
bubbleDown 로직
- index = 0부터 heap 길이만큼 순환
1. 좌, 우 자식 중 큰 자식 구함
2. 큰 자식과 부모와 비교
3. if 부모 > 큰 자식 => break
else => 부모와 큰 자식 swap
heap 정렬이 이미 된 heap = [9, 8, 7, 4, 5, 1]에서 빌 때까지 pop을 진행시켜 보기 이전에 동작과정을 예측해보자.
처음 heap 상태

pop 진행
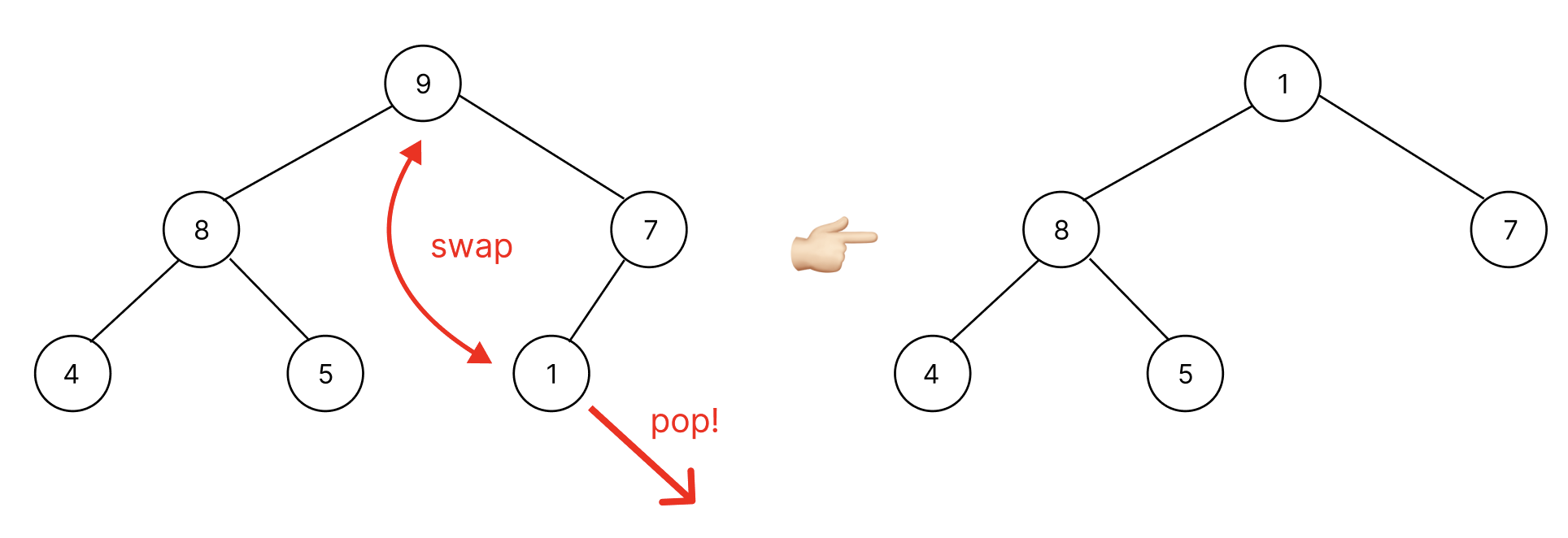
위의 처음 heap 상태에서 pop을 진행하면 root node에 존재하는 9가 마지막 노드 1과 swap 후 pop이 된다. 이후에는 1이 적절한 위치를 대소 관계 비교를 통해서 찾아야 한다.
대소관계 비교 -> bubbleDown
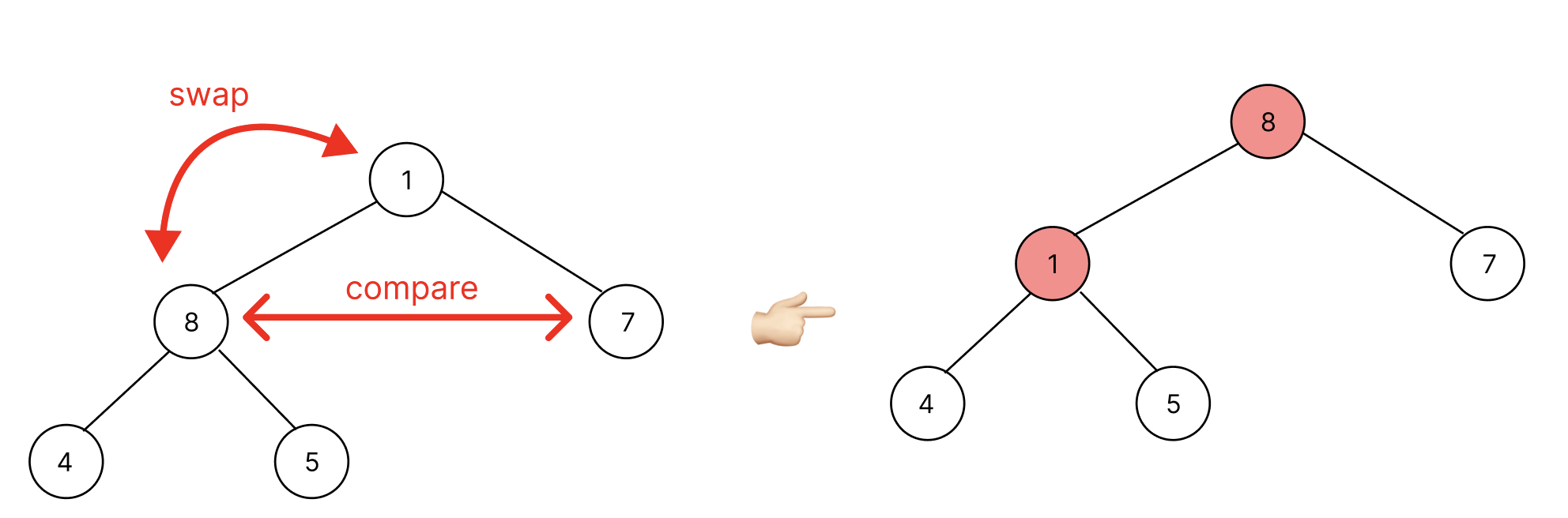
좌, 우 노드 중 왼쪽 노드(8)가 오른쪽 노드보다 크다.
부모노드(1)과 비교했을 때 왼쪽 노드가 큼으로 swap한다. 아직 적절한 위치에 놓인 것이 아니므로 계속 자식과 대소관계를 비교한다.

똑같은 과정을 거쳐서 1의 적절한 위치를 찾았다. 이러한 과정을 반복하면 pop의 순서는 9 -> 8 -> 7 -> 5 -> 4 -> 1로 예측할 수 있다. 이제 구현과 테스트로 검증해보자.
구현
// bubbleDown
class Heap {
...//
pop() {
if (this.heap.length > 0) {
this.swap(0, this.heap.length - 1);
const poppedValue = this.heap.pop();
this.bubbleDown(0);
return poppedValue;
}
return null;
}
bubbleDown(parentPos) {
let largestPos = parentPos * 2 + 1; // 왼쪽 자식 위치이자 자식 중 큰 위치
const parentValue = this.heap[parentPos];
while (largestPos < this.heap.length) {
const rightPost = largestPos + 1;
// heap의 길이보다 작다는 것은 오른쪽 자식 노드가 존재한다는 의미.
if (rightPost < this.heap.length) {
this.heap[rightPost] > this.heap[largestPos] && (largestPos = rightPost);
}
// 부모가 좌, 우 자식 모두보다 크다면 적절한 위치를 찾음
if (this.heap[largestPos] < this.heap[parentPos]) break;
this.swap(largestPos, parentPos);
parentPos = largestPos;
largestPos = parentPos * 2 + 1;
}
}// test
const arr = [9, 8, 7, 4, 5, 1];
const heap = new Heap(arr);
let popRoutes = ''
while (heap.heap.length > 0){
popRoutes += `${heap.pop()} -> `
}
console.log(popRoutes.slice(0, popRoutes.length - 4)); // 9 -> 8 -> 7 -> 5 -> 4 -> 1
heap에서의 pop과정 애니메이션

3️⃣ heapify(O(N))
heapify는 배열로 들어온 데이터를 heap구조로 변환하는 작업을 수행하는 함수이다. 이를 어떻게 구현해야할까 생각하다가 파이썬 라이브러리 구현부에서 흰트를 얻을 수 있었다.

reversed(range(n//2))가 대체 무엇을 뜻하는지 생각해보다가 스스로 컴퓨터가 되어 heapify를 진행하려면 어떻게 해야할까 생각하다가 알았다. 기존에 들어온 배열을 heap구조로 변환하기 위해서는 subTree에서 bubbleDown을 재귀적으로 수행해야 한다. 이 때 reversed(range(n//2))는 subTree의 root node임을 알 수 있다. 좀 더 설명하자면, 초기에 [5, 4, 7, 9, 8, 1]이라는 배열이 들어온다면 완전 이진 트리로 아래와 같이 나타낼 수 있다.
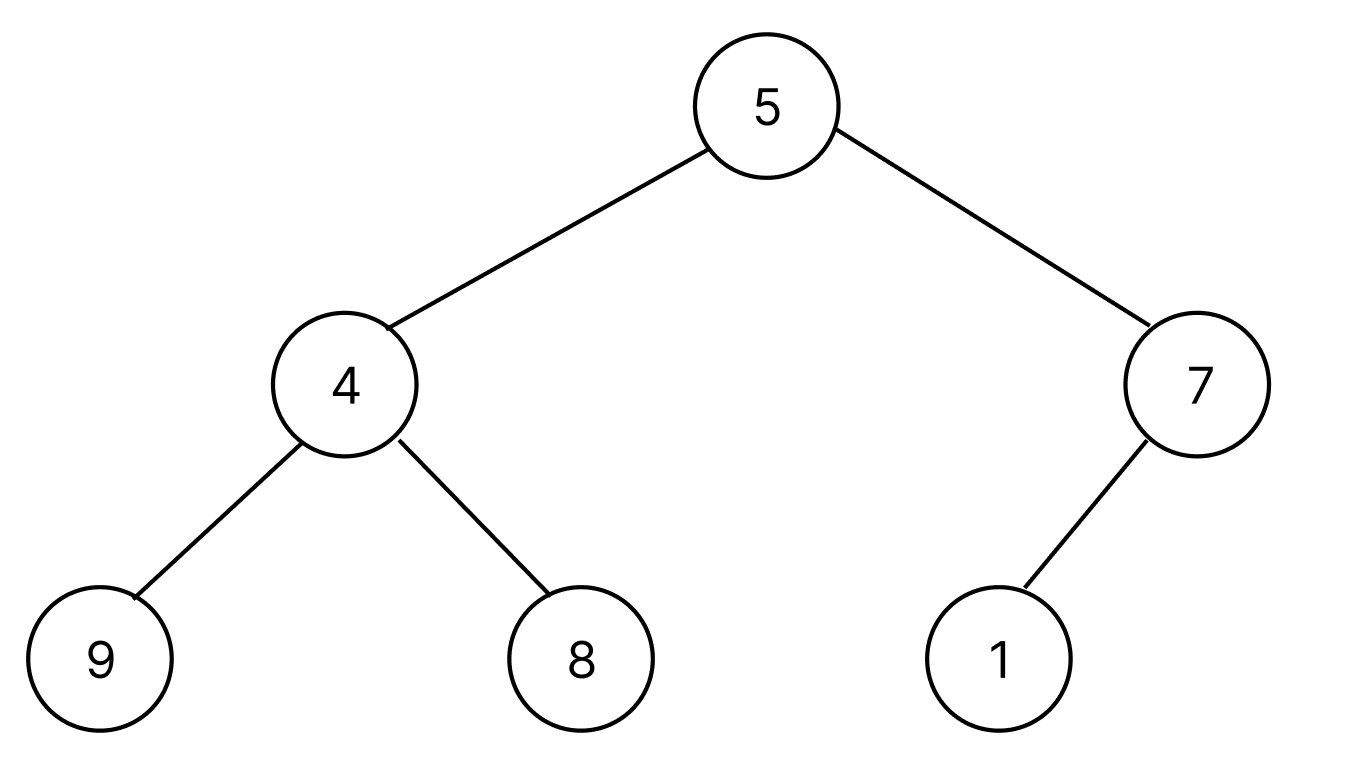
위의 트리에서 bubbleDown을 수행해야하는 subTree는 총 3개의 트리가 존재한다.
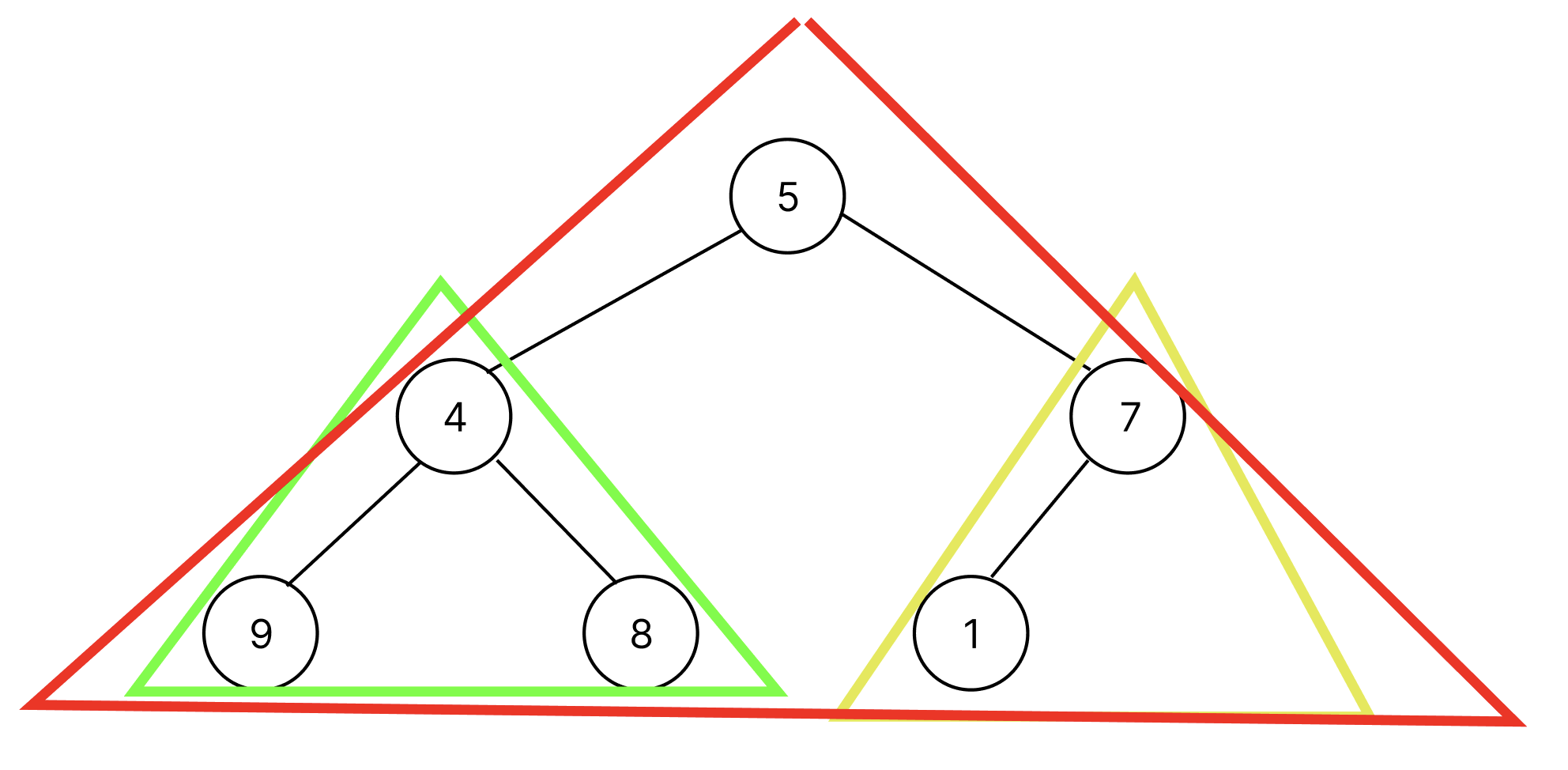
위의 reversed(range(n//2))을 여기에 도입해보면 [2, 1, 0]라는 위치값을 얻을 수 있는데 이는 subTree의 root node의 위치이다. 따라서, subTree의 root node에서 tree의 가장 깊은 깊이까지 bubbleDown을 수행하면 된다.
구현
class Heap {
...//
heapify() {
const leafParentPos = parseInt(this.heap.length / 2) - 1;
for (let parentPos = leafParentPos; parentPos >= 0; parentPos--) {
this.bubbleDown(parentPos);
}
}
bubbleDown(parentPos) {
let largestPos = parentPos * 2 + 1; // 왼쪽 자식 위치이자 자식 중 큰 위치
const parentValue = this.heap[parentPos];
while (largestPos < this.heap.length) {
const rightPost = largestPos + 1;
// heap의 길이보다 작다는 것은 오른쪽 자식 노드가 존재한다는 의미.
if (rightPost < this.heap.length) {
this.heap[rightPost] > this.heap[largestPos] && (largestPos = rightPost);
}
if (this.heap[largestPos] < this.heap[parentPos]) break;
this.swap(largestPos, parentPos);
parentPos = largestPos;
largestPos = parentPos * 2 + 1;
}
}
...//
}// test
const arr = [5, 4, 7, 9, 8, 1];
console.log('heapify 전 ', arr);
const heap = new Heap(arr).heapify();
console.log('heapify 후 ', heap.heap);
arr -> heap(heapify) 과정

전체 구현
class Heap {
constructor(heap = []) {
this.heap = heap;
this.heapify();
}
push(value) {
this.heap.push(value);
this.bubbleUp();
}
pop() {
if (this.heap.length > 0) {
this.swap(0, this.heap.length - 1);
const poppedValue = this.heap.pop();
this.bubbleDown(0);
return poppedValue;
}
return null;
}
heapify() {
const leafParentPos = parseInt(this.heap.length / 2) - 1;
for (let parentPos = leafParentPos; parentPos >= 0; parentPos--) {
this.bubbleDown(parentPos);
}
return this;
}
bubbleUp() {
let pos = this.heap.length - 1;
const pushedValue = this.heap[pos];
while (pos > 0) {
const parentPos = (pos - 1) >> 1;
const parentValue = this.heap[parentPos];
if (pushedValue > parentValue) {
this.heap[pos] = parentValue;
pos = parentPos;
continue;
}
break;
}
this.heap[pos] = pushedValue;
}
bubbleDown(parentPos) {
let largestPos = parentPos * 2 + 1; // 왼쪽 자식 위치이자 자식 중 큰 위치
const parentValue = this.heap[parentPos];
while (largestPos < this.heap.length) {
const rightPost = largestPos + 1;
// heap의 길이보다 작다는 것은 오른쪽 자식 노드가 존재한다는 의미.
if (rightPost < this.heap.length) {
this.heap[rightPost] > this.heap[largestPos] && (largestPos = rightPost);
}
if (this.heap[largestPos] < this.heap[parentPos]) break;
this.swap(largestPos, parentPos);
parentPos = largestPos;
largestPos = parentPos * 2 + 1;
}
}
swap(pos1, pos2) {
[this.heap[pos1], this.heap[pos2]] = [this.heap[pos2], this.heap[pos1]];
return true;
}
getMax() {
return this.heap[0];
}
getMin() {
return this.heap.at(-1);
}
}
✅ 정리
heap에서 push, pop에 대한 시간 복잡도는 배열에 push 또는 pop 할 때 O(1)이며, 적절한 위치에 놓이기 위해 tree의 깊이만큼 탐색을 진행하기 때문에 O(logN)이다. 그리고 heapify는 O(NlogN)으로 예측하였는데 O(N)이라고 한다. 증명은 GeekForGeeks에서 확인할 수 있다.
좀 헷갈릴 수 있는게 내가 한 힙 구현은 python에 있는 heapq 라이브러리를 기반으로 구현했기 때문에 여기서 heapify는 다른 블로그에서 말하는 build-heap과 같다. 그리고 bubbleDown & bubbleUp은 파이썬 docs의 _siftup & _siftdown과 매칭된다. 여기서 변수명이 siftup일까?? 궁금증이 생겼는데... sift는 체로 거르다라는 의미가 있다. bubbleDown을 하면 원래 위치했던 노드들이 상위로 올라가기 때문에 위로 체로 거르다라는 느낌인 것 같다.
🔥 마치며
이 블로그에서는 heap과 같이 언급되는 우선순위 queue는 따로 구현하지 않았는데 공부를 해 보니까 heap이 우선순위 queue와 별 다른 차이가 없다고 생각해서이다. 예를 들어 최대 힙 같은 경우에 가장 높은 값을 빨리빨리 얻을 수가 있는데 높은 값을 우선순위라고 가정하면 heap은 집어 넣는 데이터 구조를 제외하고 priority queue와 같다고 생각한다. 그냥 node에 priority 멤버를 주고 구현하면 된다.
heap을 공부하고 나서 중요도가 있는 TODO리스트 애플리케이션을 구현한다고 하면 sort API가 아닌 heap을 이용하면 더 빠른 UX를 제공하지 않을까 싶다.(TODO가 엄청 많다는 가정하에....?) 아니면, 응급실에서 급한 환자들을 추릴 때 heap을 이용하면 더 빨리 환자목록을 얻을 수 있을 것 같다. 그리고 다익스트라 알고리즘에서 쓰인다는데 다익스트라는 아직 공부해보지 못해서 다음에 heap을 이용해서 구현해봐야겠다.
만약에 내가 계속 python만 썼다면 이렇게 구현해야겠다???라는 생각이 들었을까 싶다. 프론트엔드 공부를 하기 위해 javascript를 익힐 겸 알고리즘을 풀기 시작한 것이 자료구조에 대해서 더 깊이 공부하는 계기가 됐다. 불편함이 나에게는 간과했던 지식을 짚고 넘어가는 기회가 되어 기분이 좋다.
📚 참고
build-heap time complexity
colt steele algorithm course
python heapq library github

