🍀 네트워크

이 문제는 네트워크의 개수를 새는 것으로 node의 개수를 세는 것이 아닌 탐색시 방문처리를 해서 문제를 풀 수 있다. 주요 로직은 한 번의 탐색마다 network += 1이 된다.

dfs와 bfs로 문제를 풀었으며 평소 풀이와 다르게 푼 부분이 있어서 기록해본다. 다르게 푼 부분은 방문을 하는 순간 간선을 끊어서 다음 탐색 대상에서 제외시키는 로직으로 구현하였다.

bfs

네트워크 내의 컴퓨터는 모두 간선으로 이어져있으므로 간선이 존재하면 탐색을 진행해 현재 방문한 컴퓨터에 대해 방문처리를 한다. 문제의 예제 #1을 예시로 들어보자.
n = 3, computers = [[1, 1, 0], [1, 1, 0], [0, 0, 1]]이라는 input을 받으면 visited = [False, False, False]와 같이 만들 수 있다. 이 때 index는 computer번호이고 값은 방문 유무이다.

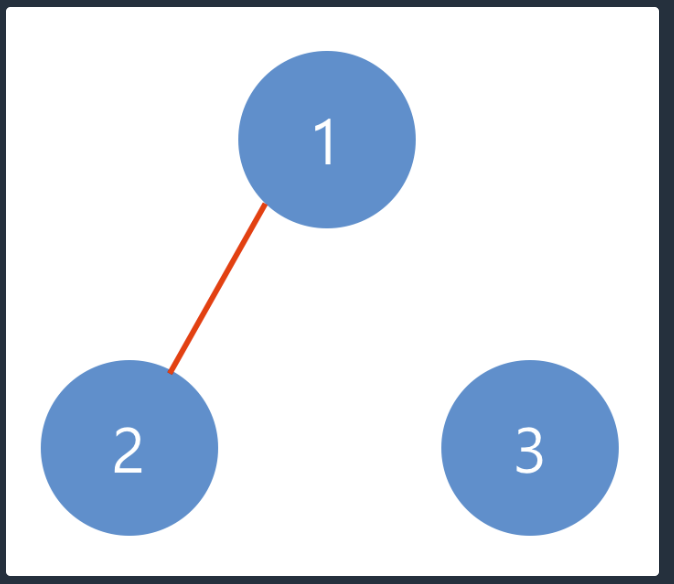
먼저 1부터 탐색을 시작하면 아래와 같은 과정을 거친다.

🚀 탐색 시작

1️⃣ computer1 방문 -> visited = [True, False, False]
computer2 방문 -> visited = [True, True, False]
더 이상 computer2와 연결된 computer는 존재하지 않으므로 network = 1

2️⃣ computer3 방문 -> visited = [True, True, True]
computer3과 연결된 computer는 존재하지 않으므로 network = 2

탐색 종료 ❌

어차피 모든 컴퓨터를 방문하기 때문에 사실상 2번 또는 3번 computer부터 시작해도 상관없다.

구현

def solution(n, computers):
    network_count = 0
    visited = [False] * n
    
    for start_computer in range(len(computers)):
        if (not visited[start_computer]):
            q = deque([start_computer])
            visited[start_computer]

            while q:
                current_node = q.popleft()

                for next_computer, connected in enumerate(computers[current_node]):
                    if (not visited[next_computer] and connected):
                        visited[next_computer] = True
                        q.append(next_computer)
                        
            network_count += 1
            
    return network_count

dfs

1️⃣ bfs -> dfs

첫 번째 풀이는 위에 bfs로 구현한 코드를 dfs로 바꾼 것이다.

def solution(n, computers):
    visited = [False for _ in range(n)]
    network_count = 0
    
    def search(current_computer):
        visited[current_computer] = True      
        
        for next_computer, connected in enumerate(computers[current_computer]):
            if (not visited[next_computer] and connected):
                search(next_computer)
        
    for computer in range(n):
        if not visited[computer]:
            search(computer)
            network_count += 1
            
            
    return network_count

2️⃣ 간선 끊어내기

두 번째 풀이는 머릿속에서 번쩍하고 떠오른 풀이가 있어서 이를 구현해 본 것이다.
방문처리를 할 필요가 없이 다음 탐색 대상에서 사전에 필터링하는 방식으로 구현했다. 즉, 컴퓨터에 방문을 하는 순간 연결된 컴퓨터와의 간선을 끊어버리는 것이다. 예를 들어 1번 컴퓨터가 2번 컴퓨터와 연결되어 있다고 가정하면 computers[1] = computers[2] = 0로 간선을 끊어낼 수 있다.

따라서 간선정보를 끊어내기 위한 cut_connect라는 함수를 구현해보자

# cut_connect 함수
def cut_connect(start, end, computers):
    computers[start][end] = computers[end][start] = 0

여기서 중요한 점은 computers는 복사본이 아닌 동일한 참조값을 가져야 한다. 이유는 복사본을 넘겨주게 된다면 특정 computer에 방문을 했어도 연결정보는 그대로 남아 있어 다음 탐색 대상 필터링이 되지 않기 때문이다.

구현

def cut_connect(start, end, computers):
    computers[start][end] = computers[end][start] = 0

    
def solution(n, computers):
    networks = []
    
    def search_network(current_computer):
        routes = [current_computer]
        cut_connect(current_computer, current_computer, computers) # ⭐️
        
        for next_computer, connected in enumerate(computers[current_computer]):
            if connected:
                cut_connect(current_computer, next_computer, computers)
                routes += search_network(next_computer)
                
        return routes
    
    for current_computer, edges in enumerate(computers):
        (sum(edges) != 0 and networks.append(search_network(current_computer))) # ⭐️

            
    return len(networks)

위의 코드에서 ⭐️를 눈여겨 보면 해당 computer와 간선이 아예 존재하지 않을 경우에 탐색을 진행(search_network)한다. sum(edges) != 0 조건을 왜 사용했을까???라는 의문이 들 수 있는데 이는 다음 네트워크를 탐색하기 위한 조건이다. 이 조건에 맞추기 위해서 자기 자신과 연결된 정보를 끊어주는 cut_connect(current_computer, current_computer, computers) 함수를 호출한 것이다. 자기 자신을 끊어주지 않는다면 예제 #1의 경우만 봐도 sum(edges) == 1이 되어 다음 네트워크를 탐색하지 못하게 된다.

🔥 마치며

머릿속에서 번쩍하고 떠올라서 이 생각을 기록하고자 글을 썼지만 실력이 느는데 있어서는 좋은 것 같지만 bfs -> dfs 풀이보다는 가독성이 떨어지는 것 같다. 나야 내가 짠 코드니까 이해를 하지만 만약에 다른 사람 또는 미래의 내가 sum(edges) != 0만 보고서는 이게 어떤 코드인가??? 라고 생각할 수 있다. 지금 생각해보니 이 값이 어떤 값인지 파악하지 위해서 변수명을 이용하면 좋을 것 같다는 생각이든다. can_search_network = sum(edges) != 0라고 변수에 담아주게되면 변수명만 보고도 "다음 네트워크 탐색이 가능한가"에 대한 정보를 유추할 수 있다. 따라서, (sum(edges) != 0 and networks.append(search_network(current_computer))) 👉🏻 can_search_network and networks.append(search_network(current_computer)))로 바꾸는 것이 가독성이 좋아보인다. 그대로 해석을 해보면 네트워크 탐색이 가능하다면 탐색을 시작해라라고 이해할 수 있다.