🍀 조이스틱
핳ㅎㅎㅎ 일단 이 문제를 푸는데 며칠이 걸렸다...;; 사실상 너무 떠오르지 않으면 풀이를 보고 나만의 코드로 맞추는 것도 좋지만, 나와 같은 사람이라면 공감할... 어떻게든 이 문제를 내 힘으로 해결해보고 싶었다. 따라서 시간을 많이 소요했지만 성취감으로부터 온 크나 큰 기쁨을 얻을 수 있었다.
일단 이 문제는 그리디 알고리즘이다. 이 문제의 포인트 중 하나는 조이스틱을 상하로 움직이는 최소값은 정해져있다는 것이다. 즉, 조이스틱을 좌우로 움직이다가 특정 위치에서 원하는 알파벳을 만드는데 움직이는 횟수는 정해져 있다는 것이다. 따라서, 메인으로 고민해야되는 부분은 좌우로 움직였을 때 최단거리로 꼭 방문해야할 A가 아니라면 A를 제외한 나머지 알파벳을 다 방문하는 것이 목표이다. 이 부분에서 상당히 애를 먹었다...🤣🤣🤣
✅ Python
1️⃣ 상하 최소값 구하기
먼저, 상하로 움직일 횟수를 구해보자. 나는 투 포인터와 알파벳길이를 세배로 증가시켜 상하로 움직일 수 있는 최소값을 구했는데... 다른 사람 풀이가 훨씬 깔끔하다. 여튼 내 풀이법을 보자면 'A -> Z'까지 이동하면서 좌, 우 포인터를 감소, 증가를 시키면서 원하는 알파벳이 나왔을 때 차이의 최소값을 return한다.
만약에 B시작점에서 Z의 값을 구한다고 하면 left -= 1, right += 1 연산을 계속 수행하다가 타겟 알파벳이 나오면 그 때 left와 right가 이동한 거리 중 최소값 구한다.

// 상하로 움직였을 때 target 알파벳에 도달할 수 있는 최소 횟수 구하는 함수
def find_up_down_min_move(target, alphabets):
start_index = 26
if target == 'A':
return 0
for i in range(1, 27):
left_index, right_index = start_index - i, start_index + i
if alphabets[left_index] == target or alphabets[right_index] == target:
break
return min(abs(start_index - left_index), abs(start_index - right_index))
def solution(name):
triple_alphabets = [chr(alpha_num) for alpha_num in range(65, 91)] * 3
target_alphabets_counter = {c: find_up_down_min_move(c, triple_alphabets) for c in name}
up_down_min_move = 0
for c in name:
up_down_min_move += target_alphabets_counter[c]상하 최소값 다른사람풀이
다른사람풀이에서 영감을 얻어서 내 코드에 적용해봤다. 한줄로 줄어지며 타겟 알파벳을 구하는데 O(1) 시간복잡도를 가진다...
def solution(name):
...//
target_alphabets_counter = {c: min(ord(c) - 65, 91 - ord(c)) for c in name}
up_down_min_move = 0
for c in name:
up_down_min_move += target_alphabets_counter[c]
...//2️⃣ 좌우 최소값 구하기
좌우 최소값을 구할 때 커서가 앞에 있을 때 뒤로 이동하는 것은 고려했지만 한 가지를 고려하지 못 해서 문제 푸는데 있어서 시간이 오래걸렸다 ㅜㅜ
- 커서가 뒤에 있을 때 뒤 -> 앞으로 이동 시를 고려하지 못 함.
반례 TC 👉🏻 "BABBAAAABA" 일때
좌우 최소값을 구하기 위해서는 총 3가지 거리이동을 고려해야한다.
- 정방향으로 커서를 계속 이동시키는 경우
- 커서가 앞으로 갔다가 뒤로 가는 경우
- 커서가 뒤로 갔다가 앞으로 가는 경우
그리고 로직이 복잡하여 주요한 로직을 담당하는 변수명을 설명하고 넘어가겠다.
- current_cursor_idx: 현재 커서가 있는 곳의 위치
- next_idx: 이 변수는 2가지 의미가 있다.
1. 앞 -> 뒤로 갈 때 다음으로 방문해야할 위치
2. 뒤 -> 앞으로 갈 때는 뒤에서 탐색했을 때 마지막으로 A가 아닌 알파벳이 나오는 위치- forward_to_back_distance:
앞 -> 뒤로 움직이고 있는 상황에서문자열의 뒤로 돌아갈 때 커서가 이동해야하는 거리- back_to_forward_distance:
뒤 -> 앞로 움직이고 있는 상황에서문자열의 앞으로 돌아갈 때 커서가 이동해야하는 거리
1. 정방향(앞 -> 뒤)로 가는 경우
시작지점인 index = 0으로 고정되어 있으므로 정방향으로 갈 때 문자열 뒤에서 처음으로 탐색했을 때 A가 나오지 않는 index의 위치가 최단거리가 된다.
2. 앞으로 갔다가 뒤로 가는 경우(forward_to_back_distance)
앞으로 갔다가 뒤로가는 경우의 변수를 forward_to_back_distance라 하면 2 * current_cursor_idx + len(name) - next_idx라는 식을 얻을 수 있다.
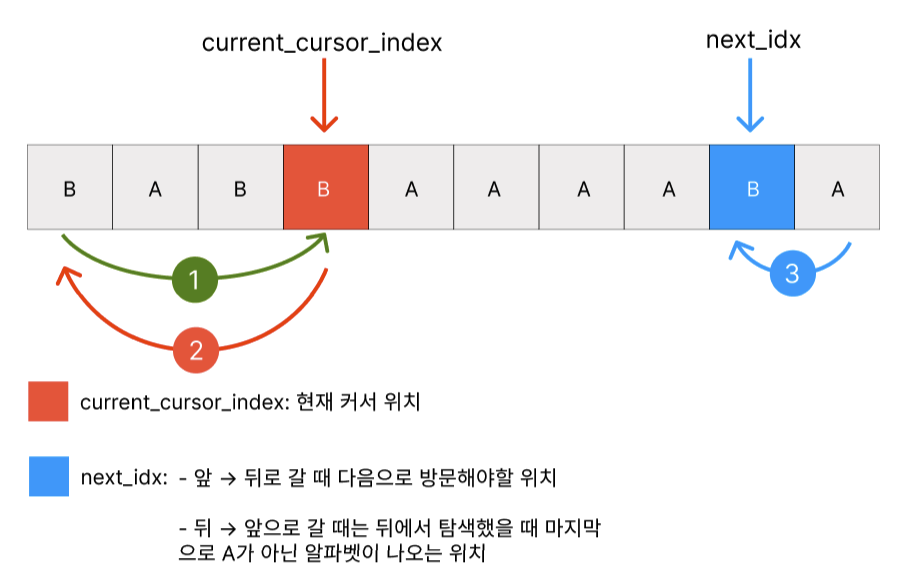
커서는 처음에 index = 0인 위치에서 1 -> 2 -> 3 순으로 이동한다. (위의 그림에서는 start = current_cursor_idx)
🔎 거리계산
① + ②: 1번과 2번의 거리는 각각 3으로 더하면2 * current_cursor_idx = 6이다③: 3번의 거리는
len(name) - next_idx = 2따라서, 총 거리는
2 * current_cursor_idx + len(name) - next_idx = 6 + 2 = 8
3. 뒤로 갔다가 앞으로 가는 경우(back_to_forward_distance)
뒤로 갔다가 앞으로가는 경우의 변수를 back_to_forward_distance라 하면 2 * (len(name) - next_idx) + current_cursor_idx라는 식을 얻을 수 있다.
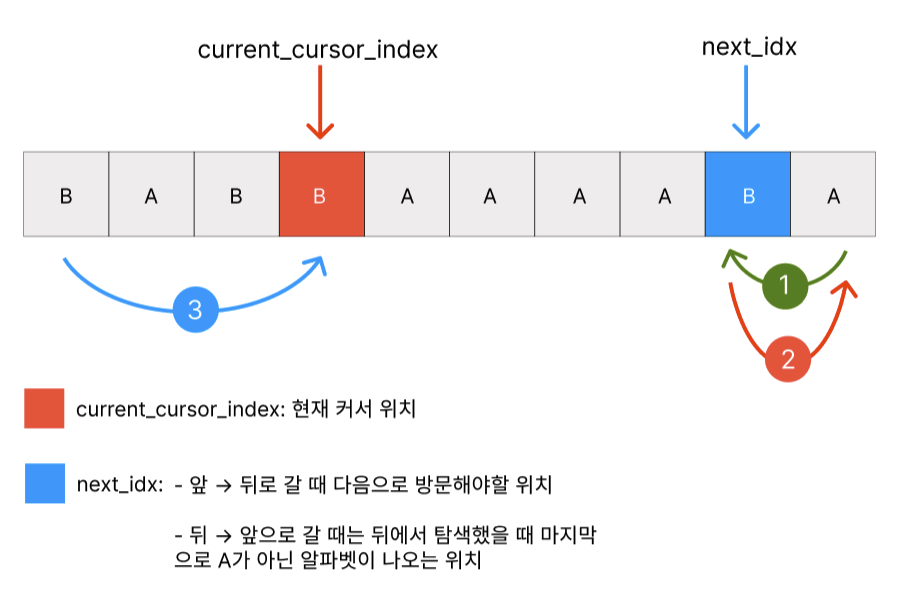
커서는 처음에 index = 0인 위치에서 1 -> 2 -> 3 순으로 이동한다. (위의 그림에서는 start = current_cursor_idx)
🔎 거리계산
① + ②: 1번과 2번의 거리는 각각 2으로 더하면2 * (len(name) - next_idx) = 4이다③: 3번의 거리는
current_cursor_idx = 3따라서, 총 거리는
2 * (len(name) - next_idx) + current_cursor_idx = 4 + 3 = 7
🛠️ 구현
이를 구현하기에 앞서서 정방향(앞 -> 뒤)로 가는 경우를 구하기 위해 마지막에서 'A'가 아닌 알파벳이 나온 위치를 구해야 한다. 'A'가 아닌 알파벳을 구하는 이유는 'A'위치에서는 상하조작을 할 필요가 없어 최대한 방문을 하지 않는 것이 좌우 거리를 최소로 만드는 중요한 요인으로서 작용하기 때문이다.
def find_index_notA_from_rear(arr):
for idx in range(len(arr) - 1, -1, -1):
if arr[idx] != 'A':
return idx
return 0이제 구현만 하면 된다. 여기서 next_idx는 다음으로 탐색할 알파벳의 위치로 'A'가 아닌 곳이 나올 때까지 1씩 증가시켜주면서 각 위치에서 앞 -> 뒤, 뒤 -> 앞으로 이동할 때 거리를 구해 최소 값을 구해주면 된다. 즉, 위에서 언급한 1. 정방향(앞 -> 뒤)로 가는 경우 2. 앞으로 갔다가 뒤로 가는 경우 3.뒤로 갔다가 앞으로 가는 경우 중에 최소값이 현재 위치에서 'A'를 제외한 알파벳을 모두 방문할 수 있는 최단거리가 된다.
전체코드는 아래와 같다.
def find_index_notA_from_rear(arr):
for idx in range(len(arr) - 1, -1, -1):
if arr[idx] != 'A':
return idx
return 0
def solution(name):
triple_alphabets = [chr(alpha_num) for alpha_num in range(65, 91)] * 3
target_alphabets_counter = {c: min(ord(c) - 65, 91 - ord(c)) for c in name}
up_down_min_move = 0
for c in name:
up_down_min_move += target_alphabets_counter[c]
last_notA_index = find_index_notA_from_rear(name)
def get_left_right_min_move(current_cursor_idx):
if current_cursor_idx == last_notA_index: return last_notA_index
next_idx = current_cursor_idx + 1
while next_idx < last_notA_index:
if name[next_idx] != 'A':
break
next_idx += 1
forward_to_back_distance = 2 * current_cursor_idx + len(name) - next_idx
back_to_forward_distance = 2 * (len(name) - next_idx) + current_cursor_idx
min_cursor_moved = min(forward_to_back_distance, back_to_forward_distance)
return min(min_cursor_moved, get_left_right_min_move(next_idx))
return up_down_min_move + get_left_right_min_move(0)동작원리를 살펴보자
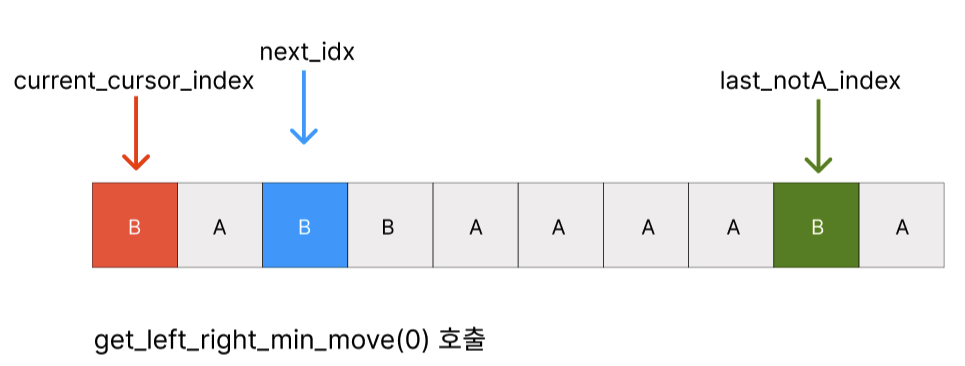
forward_to_back_distance: 8
back_to_forward_distance: 16
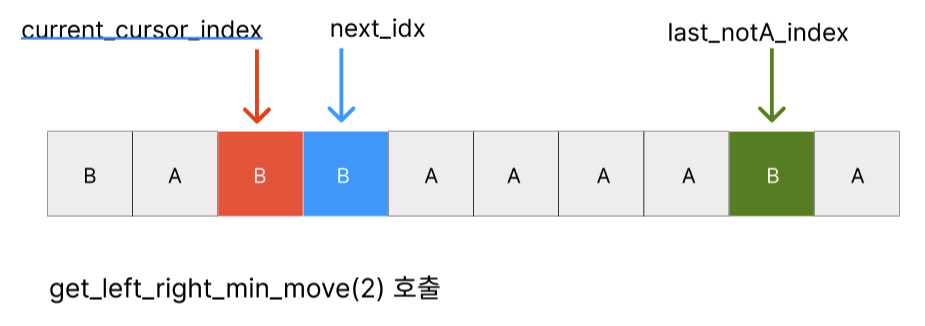
forward_to_back_distance: 11
back_to_forward_distance: 16
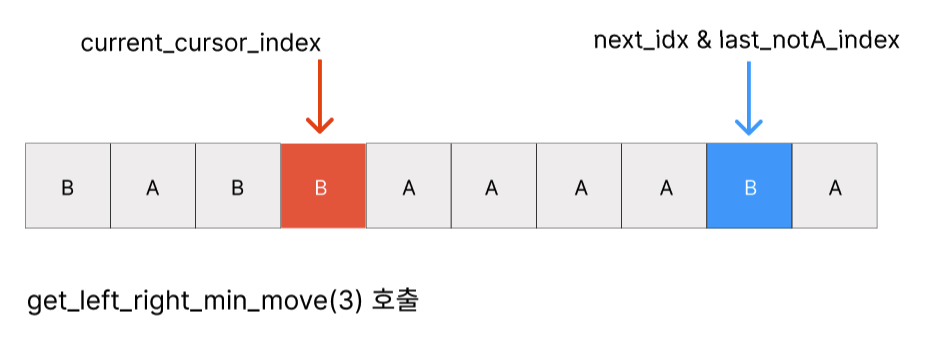
forward_to_back_distance: 8
back_to_forward_distance: 7
이후 탐색이 끝나고 좌우의 최소 이동거리는 7이 되고 상하의 최소이동거리는 4가 되어 모든 커서의 최소 이동거리는 11이 된다. 재귀를 써서 무작정 추측하면 O(N^2)과 가까운 것으로 생각되지만 사실상, 이 코드의 시간 복잡도는 O(N)이 된다.
🔥 마치며
이 문제가 왜 level2인지 모르겠다.... TC가 추가된 후 다른사람풀이가 통과되지 않는 코드가 많이 있다. 이 문제를 푸는데 3일 내내 길가다가 밥 먹다가 수시로 떠 올랐다... 🤣🥺
문제풀이를 완료하고 블로그를 쓰는 이 시점은 거의 1주일이 지나서 쓰는데 다시 코드를 짜고 이해하는데 시간도 걸렸을 뿐더러 블로그를 쓰면서 준비할 자료 및 중간에 꼬여서 다시 쓰는 등 어마무시한 시간이 걸렸다. 되게 큰 성취감을 가져다 준 문제이지만 공부할게 많은데 이것만 붙잡고 있는 것이 맞나 싶은 생각도 양방향으로 들게된다. 어떻게 공부하는게 효율적인가 생각이 들지만 결국엔 성장하는데 있어 이러한 과정은 매우 중요한 양분이 되지 않을까 싶은 생각을 하면서 블로그를 마무리 해 본다.

