🚀 Tree
tree는 데이터를 나타내는 자료구조 중 하나이다. 말 그대로 나무를 본따서 데이터를 구조화 했다. 우리가 보는 나무와는 달리 거꾸로 뒤집힌 나무를 생각한 것이 우리가 자료구조에서 말하는 트리 구조이다. 그리고 Tree 구조는 선형(linear)구조인 list와 달리 비선형(non-linear) 구조이다.
list ⇒ linear structure
tree ⇒ nonlinear structure
그렇다면 트리 구조는 어디에 쓰일까??? 우리가 개발 공부를 하면서 접해봤을 것을 아래에 나열해놨다.
👉🏻 트리 구조를 가지는 예
- HTML DOM: element끼리 부모-자식 관계를 이루고 있으며 window라는 최상단에 위치하는 객체(rootNode)를 가진다.
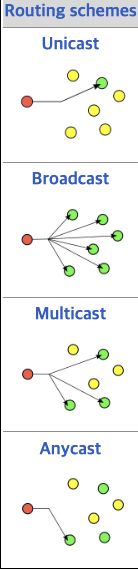
- Network Routing: routing을 할 때 트리구조로 이루어진 것을 통해서 소통이 가능하다.
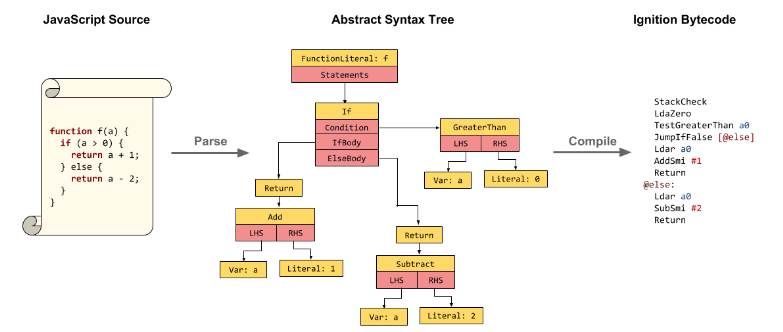
- AST(Abstract Syntax Tree): javascript를 compile할 때 중간언어인 byteword로 변환하는 과정에서 AST가 생성된다. (javascript → AST → byteword → machine code)
- Artificial Intelligence: 바둑을 두는 알파고는 바둑알을 두었을 때 경우의 수를 tree구조로 생각한다.
- folders in operating systems
- JSON File
<widipedia network routing image>
<v8.dev blog AST image>
<slide share page AST image>

<wikipedia AST image>
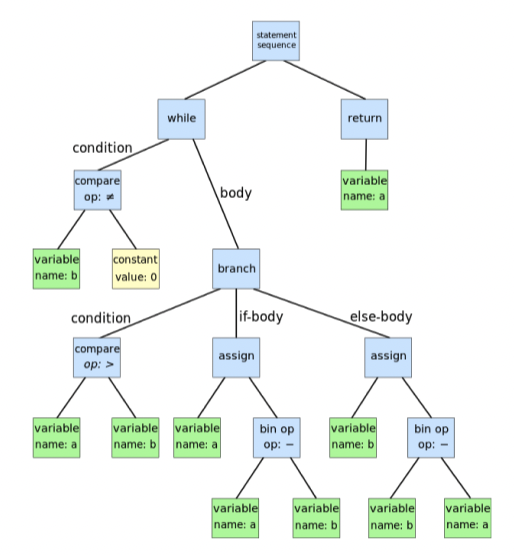
트리 용어(Tree Terminology)
- Root: 트리의 최상단 노드
- Child: 부모보다 아래에 있는 노드
- Parent: 자식을 가리키고 있는 노드
- sibling: 동일 선상에 놓인 노드
- Leaf: 자식이 없는 노드
- Edge: 노드와 노드를 연결한 선
- Node: edge로 연결되어 있으며 데이터가 저장됨. Vertex라고도 불림
- Height: tree의 높이를 나타내며 left node의 height는 0이며 부모단계를 거슬러 올라갈때마다 height는 높아진다. 즉, leaf node에서 root node까지 height를 구한다면 leaf node에서 root node까지 거친 edge의 개수가 height이다.
- Depth: tree의 깊이를 나타내며 Height와 반대로 생각하면 된다.
- Level: 아파트의 층수를 생각하면 쉽다. root node(level0)이고 leaf node(level3)라고 하면, 같은 층에 존재하는 노드들은 sibling node가 된다.
🍀 트리의 종류
트리의 종류에는 엄청 많지만…(widipedia에 있음) 난 Tree, Binary Tree, Binary Search Tree 총 3가지만 가지고 다룰 생각이며 특히 BST에 대해서 다룰 생각이다.
tree를 다루기 이전에 tree가 가지는 특징 을 염두해 두고 공부하자.
💡 tree의 특징
- 형제끼리 연결되어있으면 안 된다.
- 부모 → 자식 ⭕️ 자식 → 부모 ❌
- rootNode는 한 개여야 한다.
- 부모에서 자식으로 데이터가 흐르는
단방향계층적 구조이다.
일반트리
⇒ 위에 언급한 트리의 특징 을 만족하면서 부모가 가지는 자식노드의 개수는 제한이 없다.
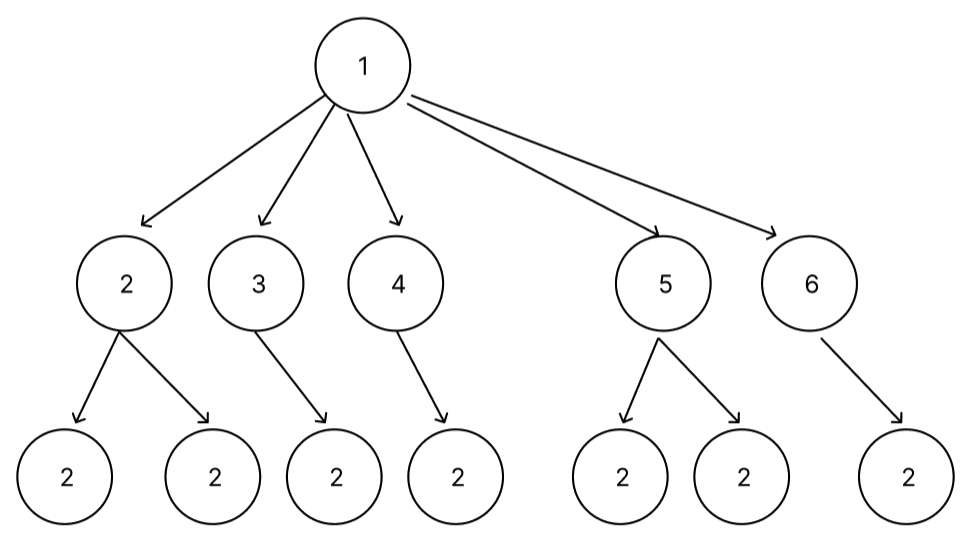
이진트리(Binary Tree)
⇒ 부모노드가 가질 수 있는 자식의 개수는 0, 1, 2 중 하나이다.
👇 이진트리 ⭕️
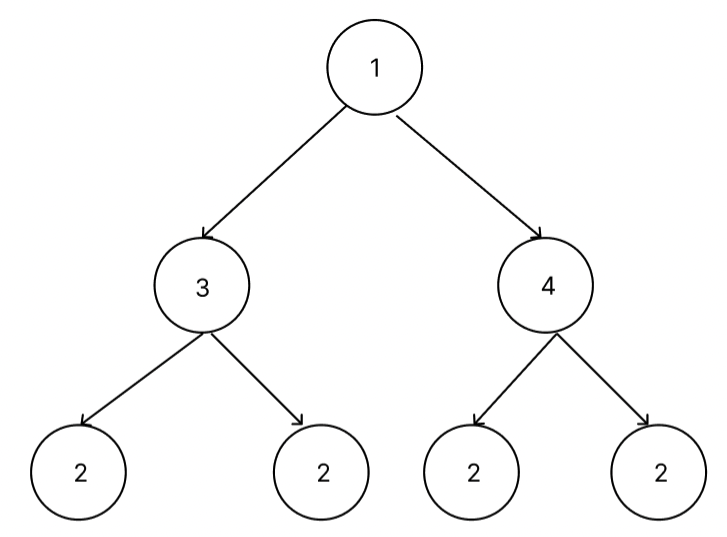
👇 이진트리 ❌ ⇒ 부모가 3개 자식을 가질 수 없다.
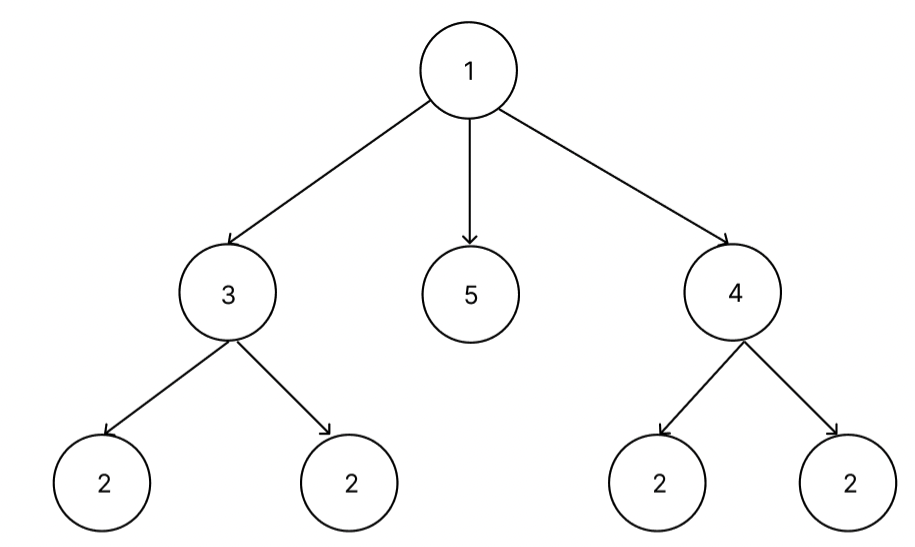
이진탐색트리(Binary Search Tree)
이진탐색트리는 이진탐색(Binary Search)과 연결리스트(Linked List)를 결합한 자료구조 형태로 이진트리구조를 가지며 데이터를 비교해서 정렬 가능하게 저장한다. 이진탐색트리는 몇 가지의 조건들이 있는데 지켜져야할 조건들은 아래와 같다.
이진탐색트리를 알아보기 이전에 이진 탐색 과 연결리스트 의 특징들을 알고 넘어갈 필요가 있다.
이진탐색은 탐색에 있어서 O(logn) 시간 복잡도를 가지지만 입력, 삭제 가 불가능한 단점이 존재하고, 연결리스트는 입력, 삭제에 대한 시간복잡도는 O(1) 의 시간 복잡도를 가지지만 탐색에 있어서 O(n) 의 시간 복잡도를 가진다. 이진탐색트리는 위에 이진탐색의 단점과 연결리스트의 단점을 해결할 수 있는 자료구조이다. 이진탐색트리에 대한 시간 복잡도는 구현하면서 설명하겠다.
💡 이진탐색트리의 특징
- 부모노드가 가지는 값은 자식노드가 가지는 값보다 작아야한다.
- 부모노드의 값보다 작은 값들은 왼쪽서브트리에 큰 값들은 오른쪽서브트리에 위치시킨다.
- 중복된 노드가 없어야 한다.
- 모든 서브 트리는 이진트리여야 한다.
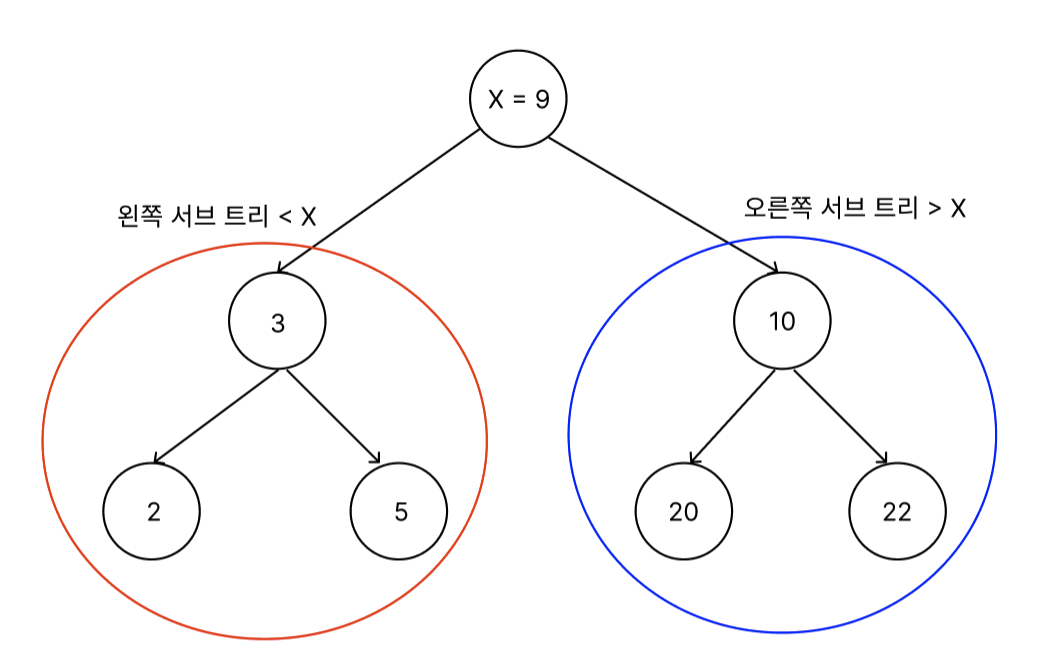
🍀 이진트리 구현
이진탐색트리 구조만 구현
class Node {
left: Node | null;
right: Node | null;
constructor(public value: number) {
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
root: Node | null = null;
constructor() {}
}
const tree = new BinarySearchTree();
tree.root = new Node(10);
tree.root.right = new Node(12);
tree.root.left = new Node(5);
tree.root.left.right = new Node(8);
console.log(tree.root);
export {};위의 코드에서 생성한 트리를 console.log로 찍어보면 아래와 같다.
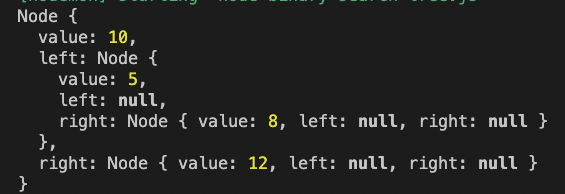
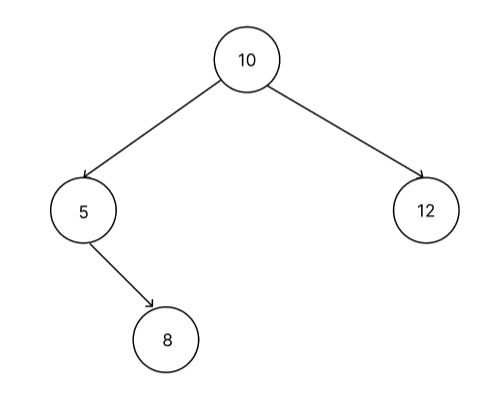
삽입
BST에서 삽입은 값의 기준으로 탐색하다가 leaf node에 추가한다. 중요한 점은 leaf node에 삽입을 한다는 것인데 트리의 중간에 노드를 삽입하게 되면 트리의 구조가 깨지기 때문이다. tree의 높이(rootNode에서 leafNode까지의 위치)를 h라 한다면 O(h) => O(logn) 의 시간 복잡도를 가진다. 여기서 leaf node에 새로운 node를 추가하는 것은 O(1) 이므로 무시할 수 있는 값이므로 시간복잡도를 계산할 때 고려하지 않아도 된다.
pseudo code
v가 삽입할 값이라고 한다면 v가 삽입되는 로직은 아래와 같이 이루어진다.
트리탐색 start
- if 삽입할 지점 found ⇒ v와 함께 새로운 노드 생성
- v > 현재 노드 값 ⇒ 오른쪽 서브트리 탐색
- v < 현재 노드 값 ⇒ 왼쪽 서브트리 탐색
insert code
class Node {
left: Node | null;
right: Node | null;
constructor(public value: number) {
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
root: Node | null = null;
constructor() {}
insert(value: number) {
const newNode = new Node(value);
if (!this.root) {
this.root = newNode;
return this;
} else {
let currentNode = this.root;
while (true) {
if (value > currentNode.value) {
if (currentNode.right === null) {
currentNode.right = newNode;
return;
}
currentNode = currentNode.right;
} else {
if (currentNode.left === null) {
currentNode.left = newNode;
return;
}
currentNode = currentNode.left;
}
}
}
}
}
const tree = new BinarySearchTree();
tree.root = new Node(10);
tree.root.right = new Node(12);
tree.root.left = new Node(5);
tree.root.left.right = new Node(8);
tree.insert(3);
tree.insert(11);
console.log(tree.root);
export {};이제 insert가 됐는지 확인보면 insert가 이진탐색트리 구조를 지키면서 나온 것을 볼 수 있다.
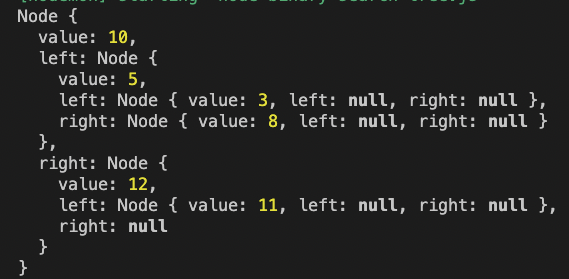
위에 console로 찍은 Tree를 시각화하면 아래와 같다.
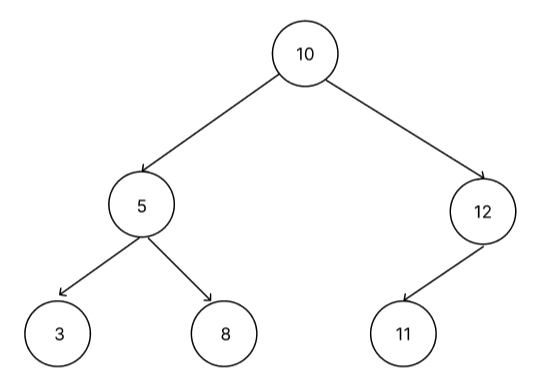
탐색(find, retrieve)
BST는 부모노드 기준으로 왼쪽은 작은 값, 오른쪽은 큰 값들이 저장되어있다. 이를 이용하면 찾고자 하는 값이 부모노드의 값보다 크다면 오른쪽으로 탐색을 하면되고, 부모노드의 값보다 작으면 왼쪽으로 탐색을 하면된다.
탐색또한 삽입과 같은 시간복잡도를 가지는데 간선을 따라 탐색을 하므로 결국 간선의 개수만큼 탐색한다. 즉, tree의 depth 또는 height과 같아 O(h) or O(logn) 의 시간 복잡도를 가진다.
pseudo code
v가 찾고자 하는 값이라고하면 탐색의 과정은 아래와 같다.
트리탐색
- if 현재 노드가 null ⇒ 찾고자 하는 값이 없으므로 return null
- if 현재 노드 값과 v가 같음 ⇒ return Node
- if v > 현재 노드 값 ⇒ 오른쪽 서브트리 탐색
- if v < 현재 노드 값 ⇒ 왼쪽 서브트리 탐색
class Node {
left: Node | null;
right: Node | null;
constructor(public value: number) {
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
root: Node | null = null;
constructor() {}
insert(value: number) {
const newNode = new Node(value);
if (!this.root) {
this.root = newNode;
return this;
} else {
let currentNode = this.root;
while (true) {
if (value > currentNode.value) {
if (currentNode.right === null) {
currentNode.right = newNode;
return;
}
currentNode = currentNode.right;
} else {
if (currentNode.left === null) {
currentNode.left = newNode;
return;
}
currentNode = currentNode.left;
}
}
}
}
find(value: number) {
let currentNode = this.root;
if (!currentNode) return null;
while (true) {
if (currentNode === null) return null;
if (currentNode.value === value) return currentNode;
currentNode = value > currentNode.value ? currentNode.right : currentNode.left;
}
}
}
const tree = new BinarySearchTree();
tree.root = new Node(10);
tree.root.right = new Node(12);
tree.root.left = new Node(5);
tree.root.left.right = new Node(8);
tree.insert(3);
tree.insert(11);
console.log(tree.find(8));
console.log(tree.find(100));8과 100을 찾은 값 출력

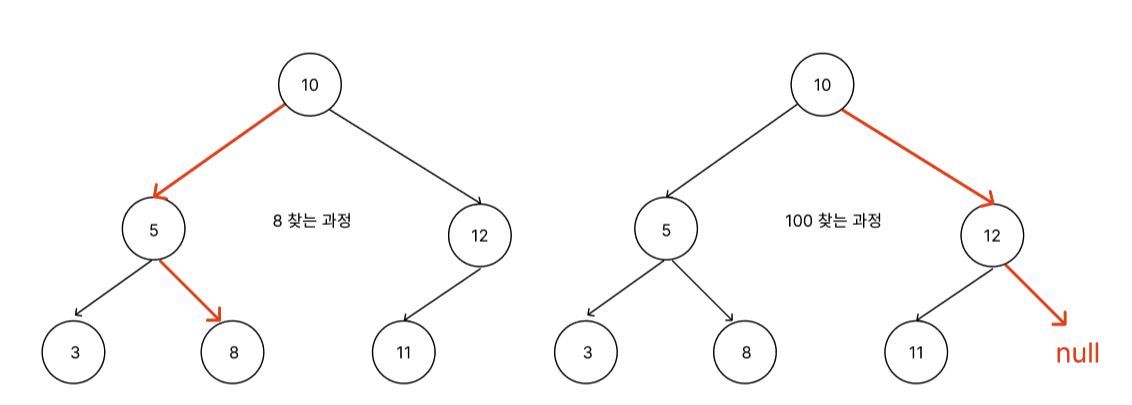
🍀 순회(Traversal)
트리를 순회하는 방법은 총 3가지 preorder(전위 순회), inorder(중위 순회), postorder(후위 순회) 가 존재한다. 트리를 순회하는데 있어서 left → right로 순회하는 공통점이 있다.
위에서 만든 BST를 가지고 순회를 진행한다.
1️⃣ PreorderTraversal(전위 순회)
전위 순회의 순서는 root-> left-> right 순서로 진행된다.
class Node<T> {
left: Node<T> | null;
right: Node<T> | null;
constructor(public value: T) {
this.left = null;
this.right = null;
}
}
class BinarySearchTree<T> {
...//
//root-> left-> right
preorderTraversal(currentNode = this.root) { // ✅ 전위 순회
if (currentNode == null) return;
console.log(currentNode.value);
this.preorderTraversal(currentNode.left);
this.preorderTraversal(currentNode.right);
}
}
const tree = new BinarySearchTree();
tree.root = new Node<number>(10);
tree.root.right = new Node<number>(12);
tree.root.left = new Node<number>(5);
tree.root.left.right = new Node<number>(8);
tree.insert(3);
tree.insert(11);
tree.preorderTraversal();
export {};전위 순회 순서
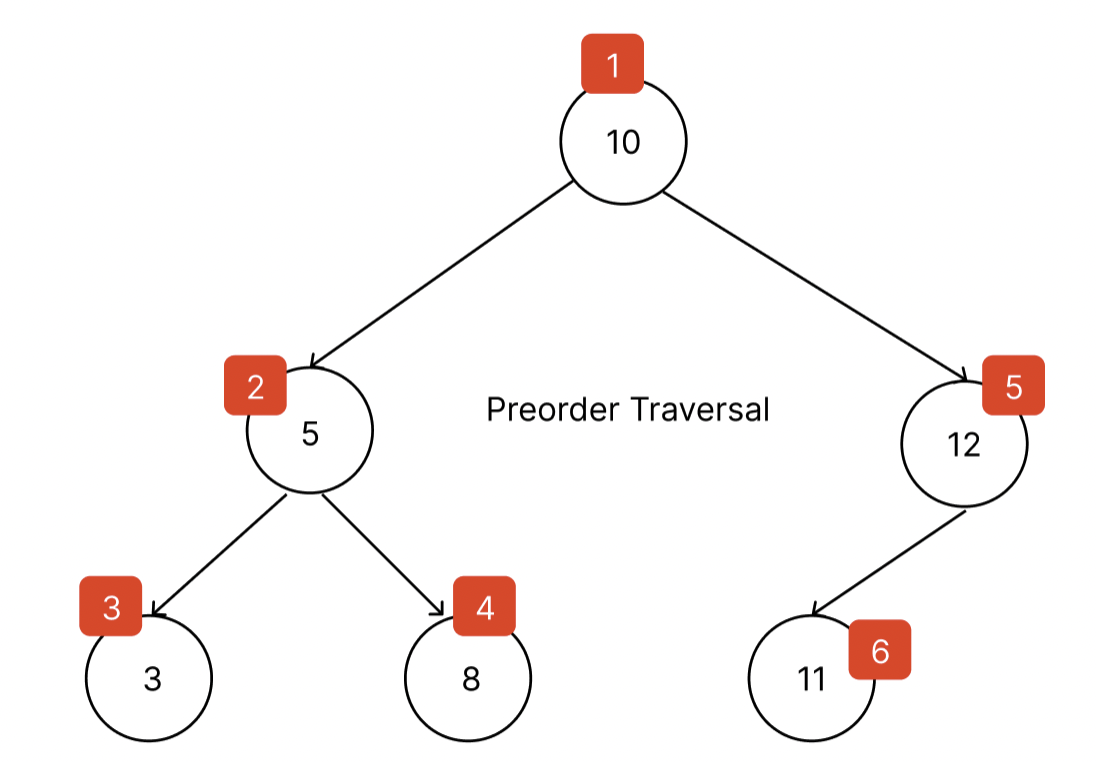
결과

2️⃣ InorderTraversal(중위 순회)
중위 순회의 순서는 left -> root -> right 순서로 진행된다.
class Node<T> {
left: Node<T> | null;
right: Node<T> | null;
constructor(public value: T) {
this.left = null;
this.right = null;
}
}
class BinarySearchTree<T> {
...//
// left -> root -> right
inorderTraversal(currentNode = this.root) { // ✅ 중위 순회
if (currentNode == null) return;
this.inorderTraversal(currentNode.left);
console.log(currentNode.value);
this.inorderTraversal(currentNode.right);
}
}
const tree = new BinarySearchTree();
tree.root = new Node<number>(10);
tree.root.right = new Node<number>(12);
tree.root.left = new Node<number>(5);
tree.root.left.right = new Node<number>(8);
tree.insert(3);
tree.insert(11);
tree.preorderTraversal();
export {};중위 순회 순서
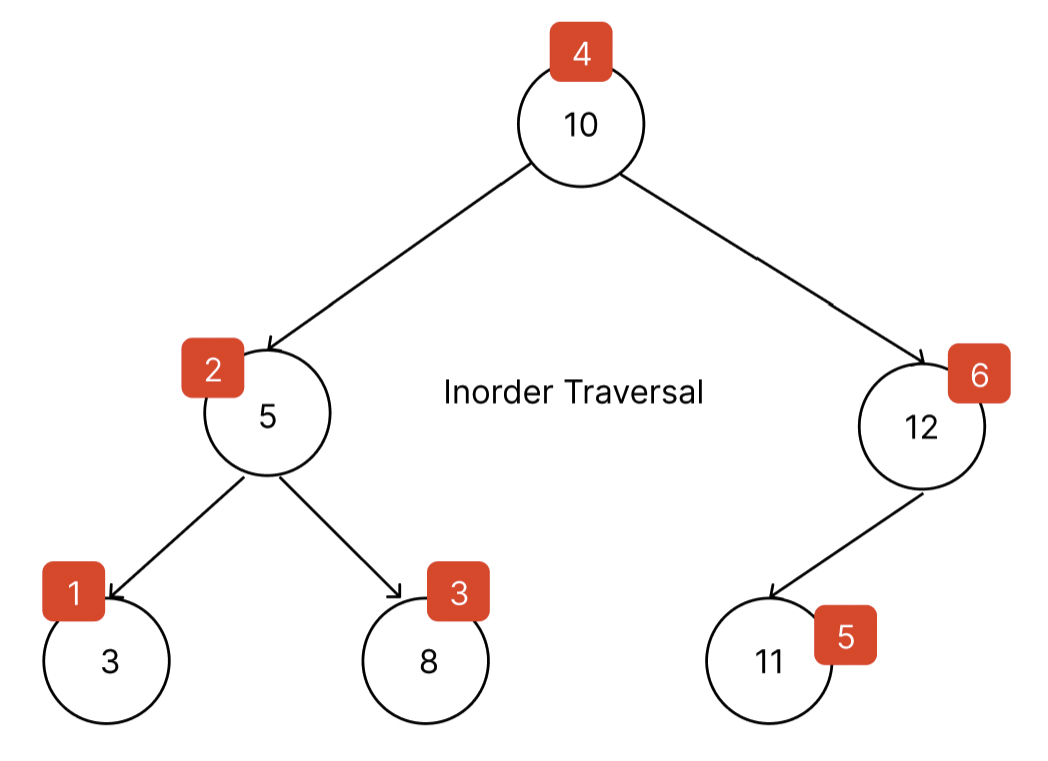
결과

3️⃣ PostorderTraversal(후위 순회)
후위 순회의 순서는 left -> right -> root 순서로 진행된다. 맨 마지막으로 root node를 순회하는 방식이다.
class Node<T> {
left: Node<T> | null;
right: Node<T> | null;
constructor(public value: T) {
this.left = null;
this.right = null;
}
}
class BinarySearchTree<T> {
...//
//left->right->root
postorderTraversal(currentNode = this.root) { // ✅ 후위 순회
if (currentNode == null) return;
this.postorderTraversal(currentNode.left);
this.postorderTraversal(currentNode.right);
console.log(currentNode.value);
}
}
const tree = new BinarySearchTree();
tree.root = new Node<number>(10);
tree.root.right = new Node<number>(12);
tree.root.left = new Node<number>(5);
tree.root.left.right = new Node<number>(8);
tree.insert(3);
tree.insert(11);
tree.preorderTraversal();
export {};후위 순회 순서
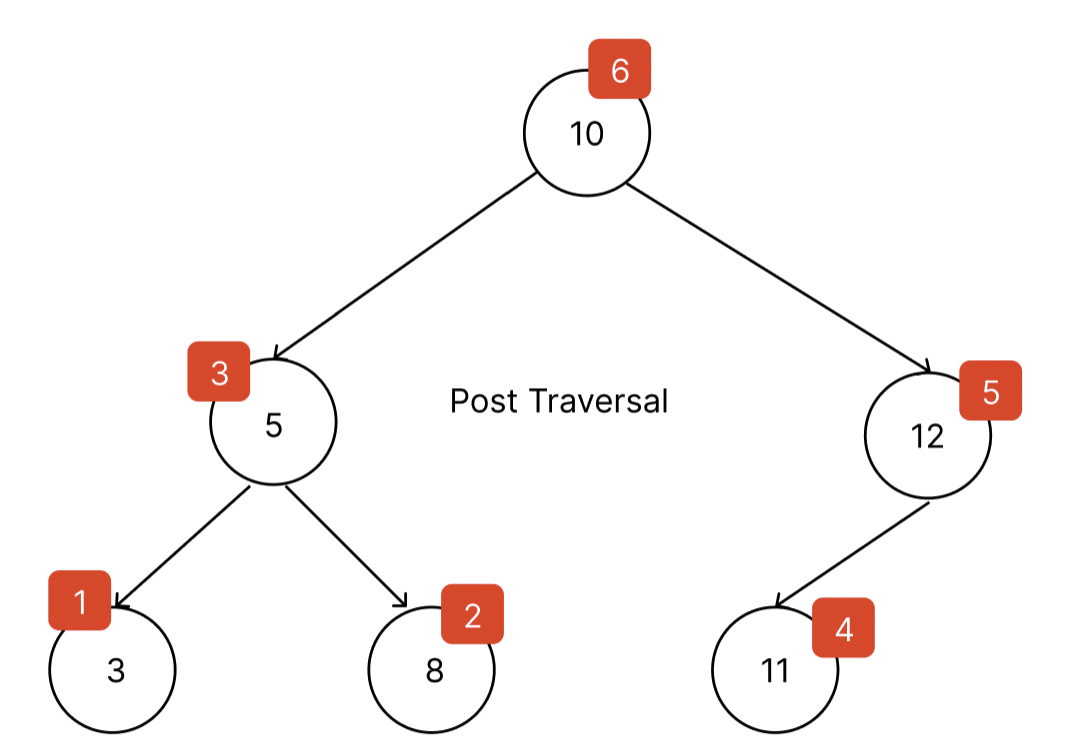
결과

🍀 O(h)가 O(logn)과 같은 이유
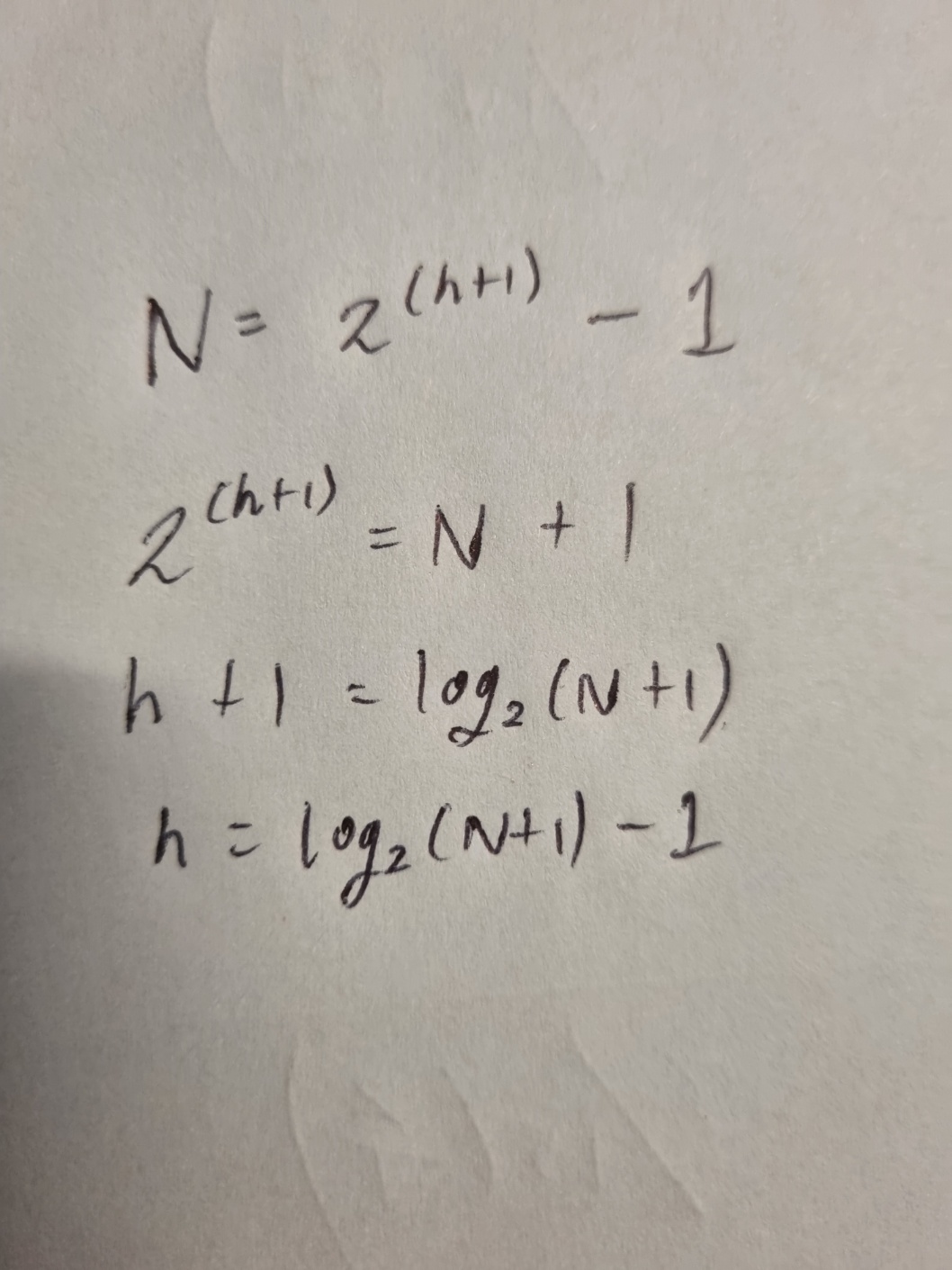
//TODO BST의 delete
📚 참고
AST(Abstract Syntax Tree)
AST slideshare page
BST(Binary Search Tree)
visualization of datastructure
tree terminology
5개의 댓글
These services may vary depending on the specific offerings of Acadian Landscaping and Tree Service, so it's always best to check with them directly for a comprehensive list of their services. https://landscapinglafayettela.com/landscaping/
These services may vary depending on the specific offerings of Acadian Landscaping and Tree Service, so it's always best to check with them directly for a comprehensive list of their services. https://landscapinglafayettela.com/landscaping/
These services may vary depending on the specific offerings of Acadian Landscaping and Tree Service, so it's always best to check with them directly for a comprehensive list of their services. https://landscapinglafayettela.com/landscaping/
These services may vary depending on the specific offerings of Acadian Landscaping and Tree Service, so it's always best to check with them directly for a comprehensive list of their services. https://landscapinglafayettela.com/landscaping/


Landscaping plays a crucial role in creating a visually appealing and functional outdoor space. Along with planting new trees and flowers, it's equally important to consider tree removal when necessary. Removing dead or diseased trees not only improves the safety of your property but also enhances the overall landscape design. tree removal peoria illinois