[DB] Functional dependency & Decomposition

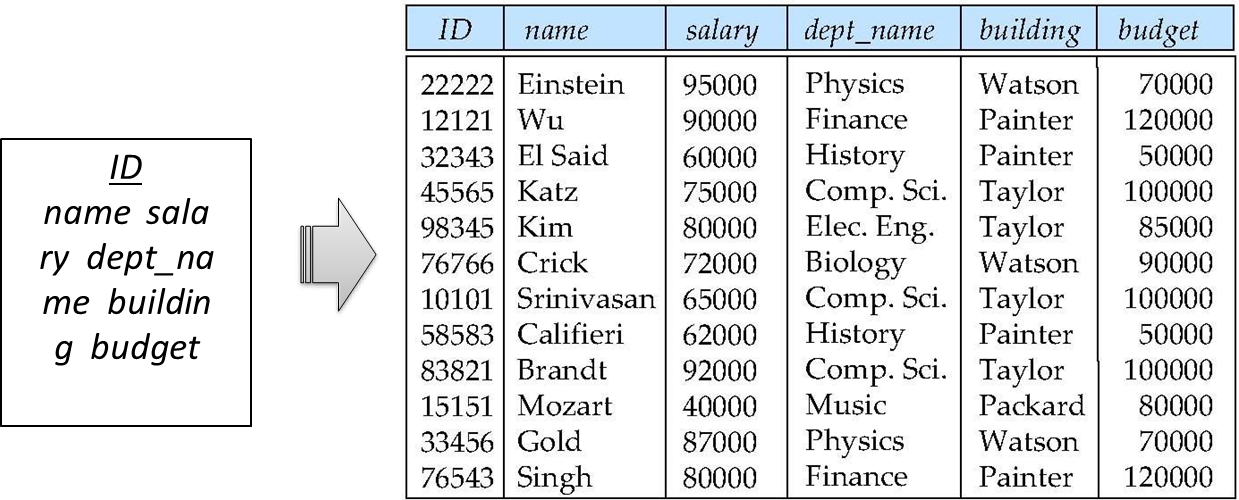
ER model을 Relational model로 변경한 후, 정규화를 수행해야한다. 데이터베이스 정규화란 현재 테이블에서 데이터 중복과 의존성을 줄이기 위한 데이터베이스 최적화이다.(relation을 쪼개어 중복을 줄이고 의존성을 최소화한다.)

데이터베이스 정규화 과정은 단계별로 이루어지며, 단계별로 요구하는 데이터베이스의 form이 존재한다. 이를 normal form이라 부르며, 이 form 조건에 다 맞추어야 정규화가 완료된다.
정규화 과정은 다음과 같다.

• First normal form(1NF)
• Second normal form(2NF): 따로 보지 않는다.
• Third normal form(3NF)/Boyce-codd normal form(BCNF)

Decomposition

decomposition 과정을 살펴보자.

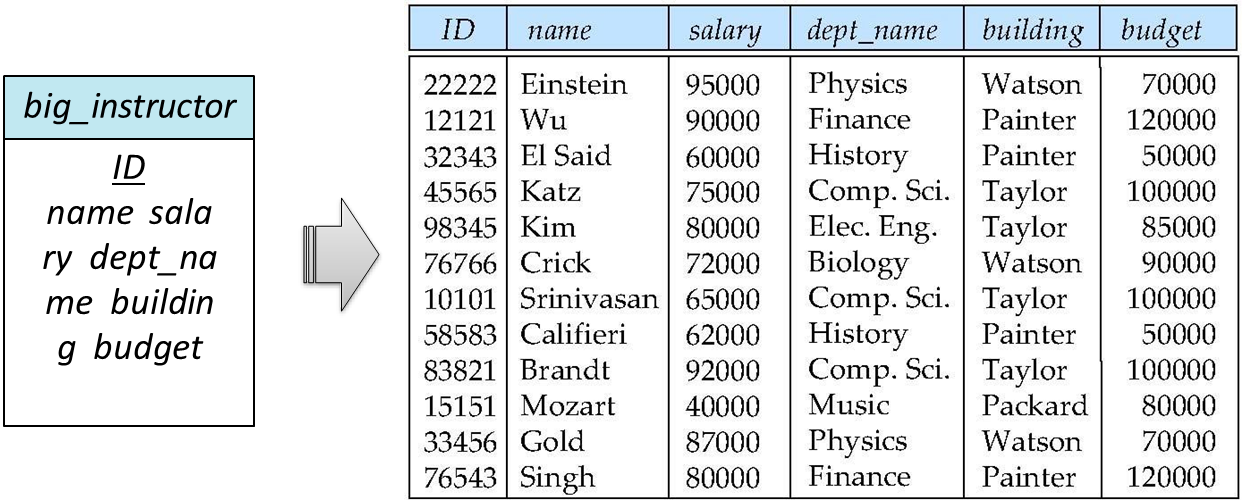
위와 같은 schema는 dept_name, building, budget이 중복되는 것을 볼 수 있다.
정보가 많으면 많을수록 DB는 커질 것이고 자원낭비가 심할 것이다.

위의 schema를 어떻게 두 개의 테이블로 나눌까? 보면 ID가 key인 것을 알 수 있고 이에 대한 나머지 attribute가 결정된다.(ID가 선택되면 이에 대한 name, salary, dept_name, building, budget이 결정된다.)
자세히 보면 dept_name도 이와 마찬가지로 dept_name이 결정되면 building과 budget이 결정되는 것을 볼 수 있다.

이를 함수 종속성(functional dependency) 기반으로 decompose 할 수 있다.
위의 내용을 함수 종속성으로 표현하면 아래와 같다.

dept_name -> building, budget

이 때 dept_name을 key로 설정하여 두 개의 table로 decompose 된다.

dept_name이 결정되면 building, budget이 결정된다는 것은 dept_name은 key라는 것이고 이는 고유한 값이다. dept_name으로 결정되는 attribute들은 어떠한 값으로 결정되어도 functional dependency를 만족한다. 이미 key로써, 유힐하기 때문이다.

ER model의 one-to-many 관계로 표현될 수 있다.

Lossless-join decomposition

분해에 대한 조건이 있다. 분해 후, join 했을 때 이전 정보가 소멸되면 안 된다는 점이다.
$\Pi_{R1}(r)⋈\Pi_{R2}(r)$ 을 수행했을 때, 이전 값과 똑같아야 한다는 것이다.

밑의 두 조건을 만족해야한다.

• $R_1\cup R_2 = R$
• $R_1 \cap R_2 \neq \varnothing$

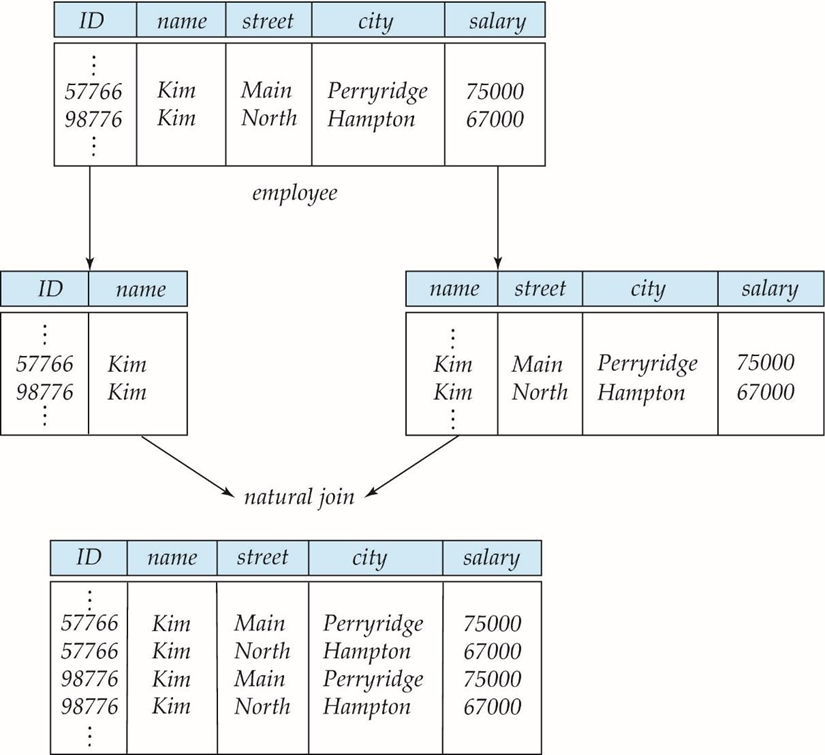
ID가 아닌, name으로 분해했을 경우, 튜플이 추가로 더 생기는 것을 볼 수 있다.
이는 잘못된 분해이며 kim에 대한 정보를 잃어버린거나 다름없다.

함수 종속성과 분해에 대해 알아보았으니, 이제 정규화를 위한 normal form을 알아보자. 이에 적용이 되어야 정규화가 잘 된 것이며, 이 포스트에선 1NF, 2NF 이후에 3NF 또는 BCNF 중 하나를 선택하는 것을 정규화 과정으로 본다.

First Normal form

1NF는 단순히 Domain(Attribute의 가능한 모든 경우의 set)이 atomic한 값이면 된다.
attribute의 값이 분리되지 않으면 된다는 것이다.

만약 강의 정보를 저장하는 table에 학수번호가 CS0012 형태로 저장되어 있으면 어떻게 될까?
application level에서 CS가 쪼개질 수 있으며, 이게 분리되어 사용된다면 atomic하지 않다. 하지만 이렇게 사용하지 않는다면 atomic하다 말할 수 있다.

Functional dependency

이제 모든 relation이 atomic한 domain을 가진다 가정한다. 그런데 R이 normal form이 아니라면, $\{R_1, R_2, ..., R_n\}$으로 분해한다.
이 때 아래의 두 조건을 만족하며 분해해야한다.

• 각각의 relation은 normal form을 만족한다.
• 분해는 lossless-join decomposition을 민족한다.

이 조건을 함수 종속성에 기반한다.

functional dependency란 유효한 table들을 구성하는 제약들이다.
relation의 특정 attribute set이 결정자 역할을 하며 다른 attribute의 set의 고유한 값을 결정한다.

즉 함수 종속성은 key 개념의 일반화인 것이다.

개념적 정의

$\alpha \subseteq R$ 그리고 $\beta \subseteq R$ 라고하자.
$\alpha \rightarrow \beta$ 라는 표현은 유효한 relation $r(R)$의 튜플 $t_1$, $t_2$에 대해 $\alpha$와 $\beta$ 모두 성립한다. 이는 아래와 같이 정리된다.
$t_1[\alpha]=t_2[\alpha] \Rightarrow t_1[\beta]=t_2[\beta]$
이는 왼쪽의 $\alpha$가 결정되면 이에 따르는 attribute $\beta$가 결정된다는 것이다.

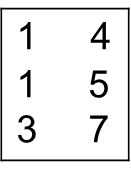
위의 r(A,B)은 $\beta \rightarrow \alpha$ 을 만족하며 이는 many-to-one 관계이다.

key의 정의

superkey

$K \rightarrow R$을 만족하면 K는 R의 superkey이다.

candidate key

$K \rightarrow R$을 만족하고 $\alpha \rightarrow R$를 만족하는 $a \subset K$가 존재하지 않으면 K는 candidate key이다.

하지만 이렇다고 항상 superkey만을 결정자로 둘 필요는 없다. normal form은 함수 종속성을 기반으로 만족함을 보일 수 있고, 이때 위에서 본 dept_name과 같은 attribute를 결정자로 두고 테스트할 수 있기 때문이다.

Use of functional dependencies

함수 종속성은 주어진 테이블에 대해 우연히 일치할 수 있는 attribute set이 존재할 수 있지만, 이게 항상 참인 것은 아니다.
함수 종속성은 주어진 relation이 유효한지 확인하기 위해 사용될 수 있다.
함수 종속성은 유효한 relation을 만족하기 위한 제약(constraints)들을 명시하기 위해 사용될 수 있다.

Trival

함수 종속성은 다음과 같을 때 trivial하다고 칭한다.

$ID, name \rightarrow ID$
$name \rightarrow name$

개념적으로 $\alpha \rightarrow \beta$ and $\beta \subseteq \alpha$ 일 때 trivial하다 칭한다.

### Back to 1NF
만약에 {phone_number} multivalued attribute는 어떻게 표현될까?
instructor의 id에 따르는 phone_number가 결정된 table을 만들면 key id에 대한 $ID \rightarrow phone\_number$를 만족하지 못하기 때문에 1NF을 만족하지 못한다.(질문)

Closure of Functional dependencies

Closure of Functional dependencies란 모든 경우의 수의 함수 종속성을 의미한다.
간략하게 함수 종속성 F에 A->B, B->C, A->D가 존재한다면 이를 확장하여 A->C, A->A 이를 모두 추가하여 모든 주어진 F에 대해 모든 경우의 수를 가지는 집합 $F^+$를 closure of functional dependency라 칭한다.