트리 Tree

📍 정의
트리는 노드로 이루어진 데이터 구조이다. 노드들 사이에 부모와 자식 관계를 가진 가지(branch)가 있다. 한 가지에서 여러개의 노드가 0~n개의 노드를 가질 수 있다. 각 노드는 한 개 이상의 다른 노드를 가리킬 수 있는 점에서 연결 리스트와는 차이가 있다. 즉 리스트는 linear 선형 구조인 반면 트리는 nonlinear 비선형 구조를 가지고 있다.
하지만 선형 구조(Singly Linked List)도 크게 보면 트리 구조에 속하므로 트리로 볼 수 있을 것이다. 만약 그렇다면 연결 리스트로 사용할테지만 굳이 따지자면.
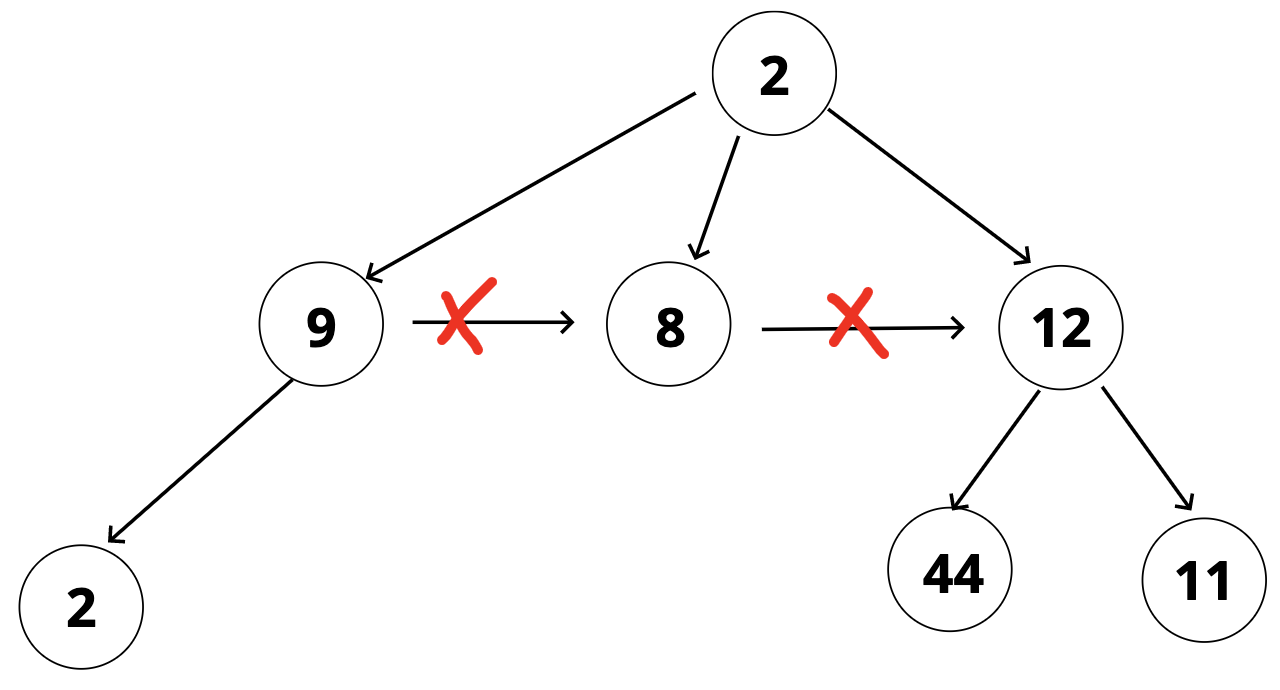
🛑 트리는 부모-자식 관계에 따라 자식 노드만 가리킬 수 있다. 다음과 같은 구조는 트리가 될 수 없다. 그래프 구조이다!
(그림1) 자식이 형제 노드를 가리키는 경우
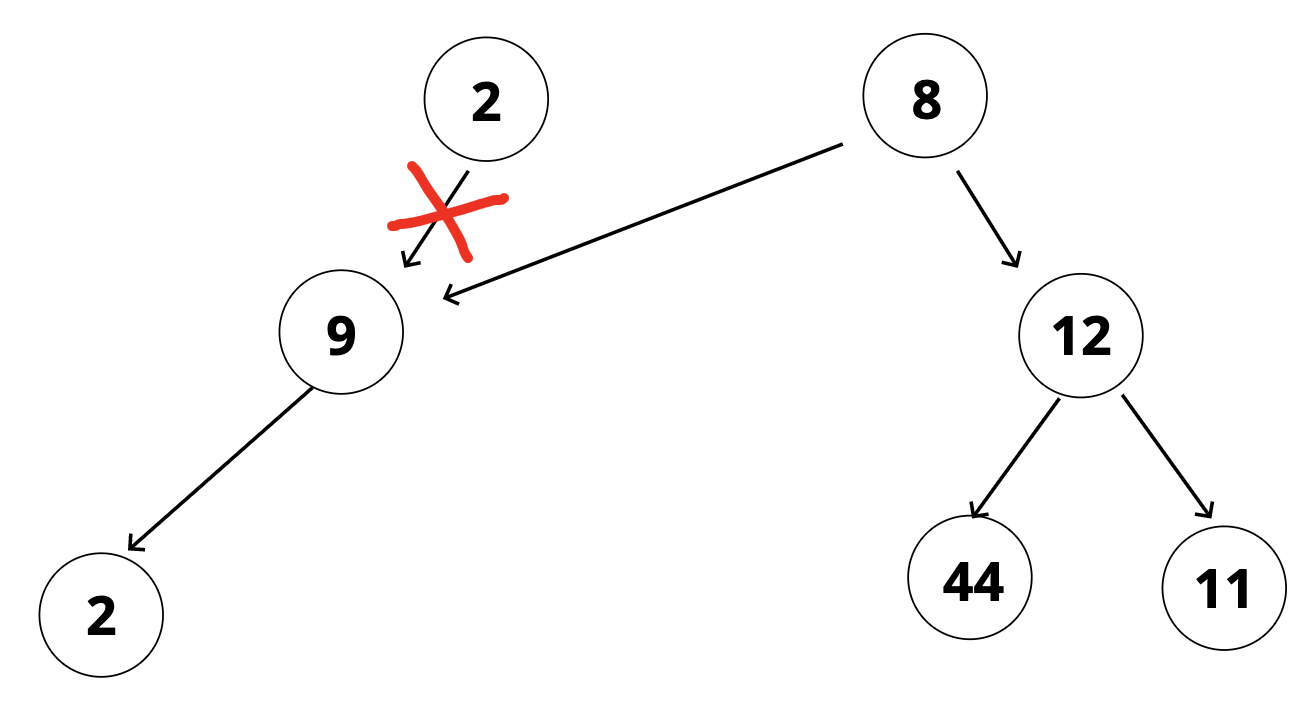
(그림2) 루트 노드가 두개인 경우
즉, 트리는 하나의 루트 노드로부터 자식노드만 가리킬 수 있으며, 루트에서 멀어지는 방향으로 연결된 노드이어야 한다.
트리의 사용 예
- HTML DOM 객체
- 유닉스/윈도우의 폴더 구조
- 네트워크 라우팅, JSON, AI 머신러닝 등 트리구조는 아주 많이 쓰인다!
- n-queen 에서도 퀸의 경우의 수를 트리 구조로 보여주었다.
dfs 백트래킹 - (사진) 알파고가 학습한 경우의 수 / 출처 google
트리의 구조, 용어
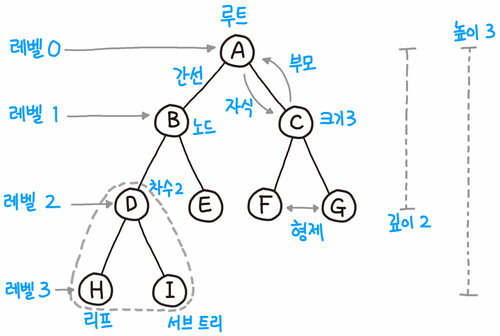
- 노드 (Node): 트리를 구성하는 기본 원소
- 루트 (Root node/Root): 트리 구조 최상단의 위치한 트리의 시작노드
- 부모노드 (Parent node): 루트 노드 방향(그림에서는 상향)으로 직접 연결된 노드
- 자식노드 (Child node): 자식노드는 루트에서 멀어지는 방향(그림에서는 하향)으로 연결된 노드.
- 형제노드 (Siblings node): 같은 부모 노드를 갖는 노드들
- 리프노드 (Leaf node): 루트 노드를 제외한 차수가 1인 정점을 의미. 즉, 자식이 없는 노드, 단말 노드라고도 한다.
- 간선 (Edge): 노드들을 잇는 선
- 길이 (Length): 출발 노드에서 도착 노드까지 거치는 간선의 갯수
- 경로 (Path): 한 노드에서 다른 노드까지 이르는 길 사이에 있는 노드들의 순서
- 깊이 (Depth): 루트 경로까지의 길이
- 레벨 (Level): 루트 노드부터 노드까지 연결된 간선 수의 합
- 차수 (Degree): 각 노드의 자식 갯수
- 크기 (Size): 노드의 갯수
- 트리의 차수 (Degree of tree): 트리의 최대 차수 max(deg1, deg2, deg3,… degn)
- 너비 (Width): 가장 많은 노드를 갖고 있는 레벨의 크기
- 포레스트 (Forest): 서로 독립적인 트리들의 모임
위 트리의 조건을 충족하면서 약간의 속성과 규칙이 더해진 정말 다양한 종류의 트리가 있다. Heap (min/max… 등) 역시 트리의 종류이다. 그 중에서도 탐색에 강점을 가지고 있는 이진 탐색 트리에 대해서 알아보자.
📍 이진 탐색 트리 BST (Binary Search Tree)
이진트리와 이진검색트리 조건
각 노드가 최대 두 개의 자식을 가질 수 있다는 규칙이 추가된다. 부모노드는 0~2개의 자식 노드를 가질 수 있다. → 이진 트리
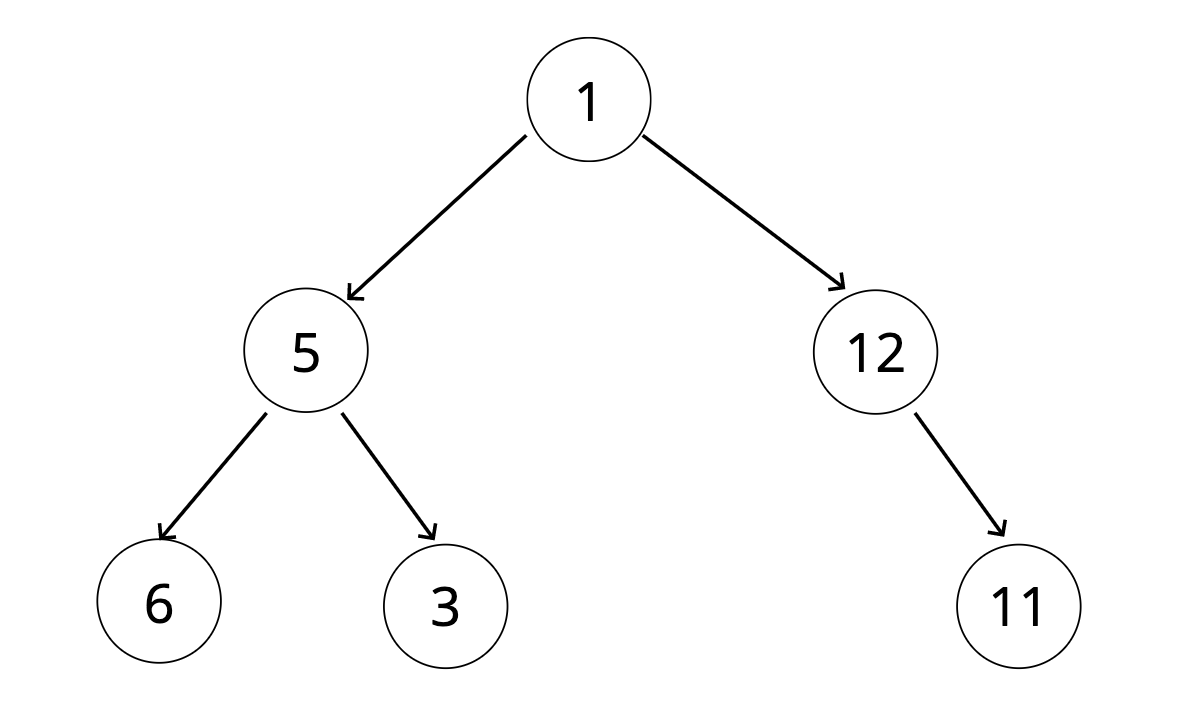
더하여, 부모 노드보다 작은 요소를 가진 노드는 왼쪽 자식 노드에 위치한다. 부모 노드보다 큰 요소는 오른쪽에 자식 노드에 위치한다. → 이진 탐색 트리
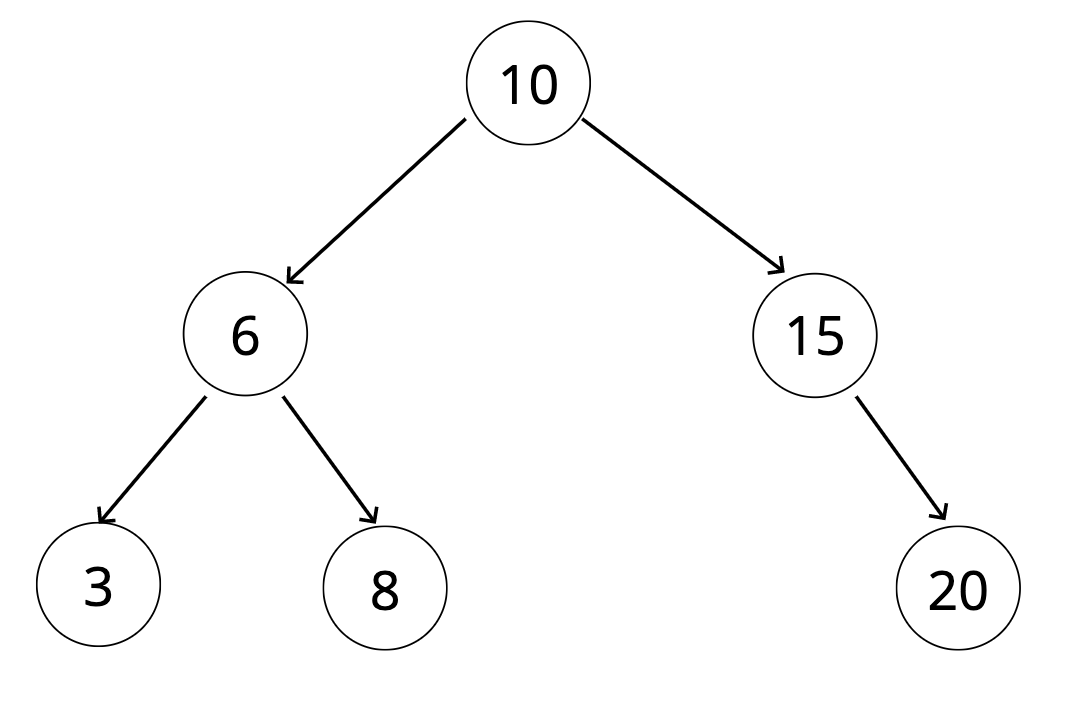
🛑 데이터가 특정 순서로 저장되기위해서는
각 노드의 요소는 (어떤 데이터이든 상관없지만) 어떤 것이 더 크고 작은지 구분할 수 있는지 비교하고 순서를 매길 수 있는 기준이 있어야 한다. (그림에서는 숫자)
이진 탐색 트리의 시간복잡도
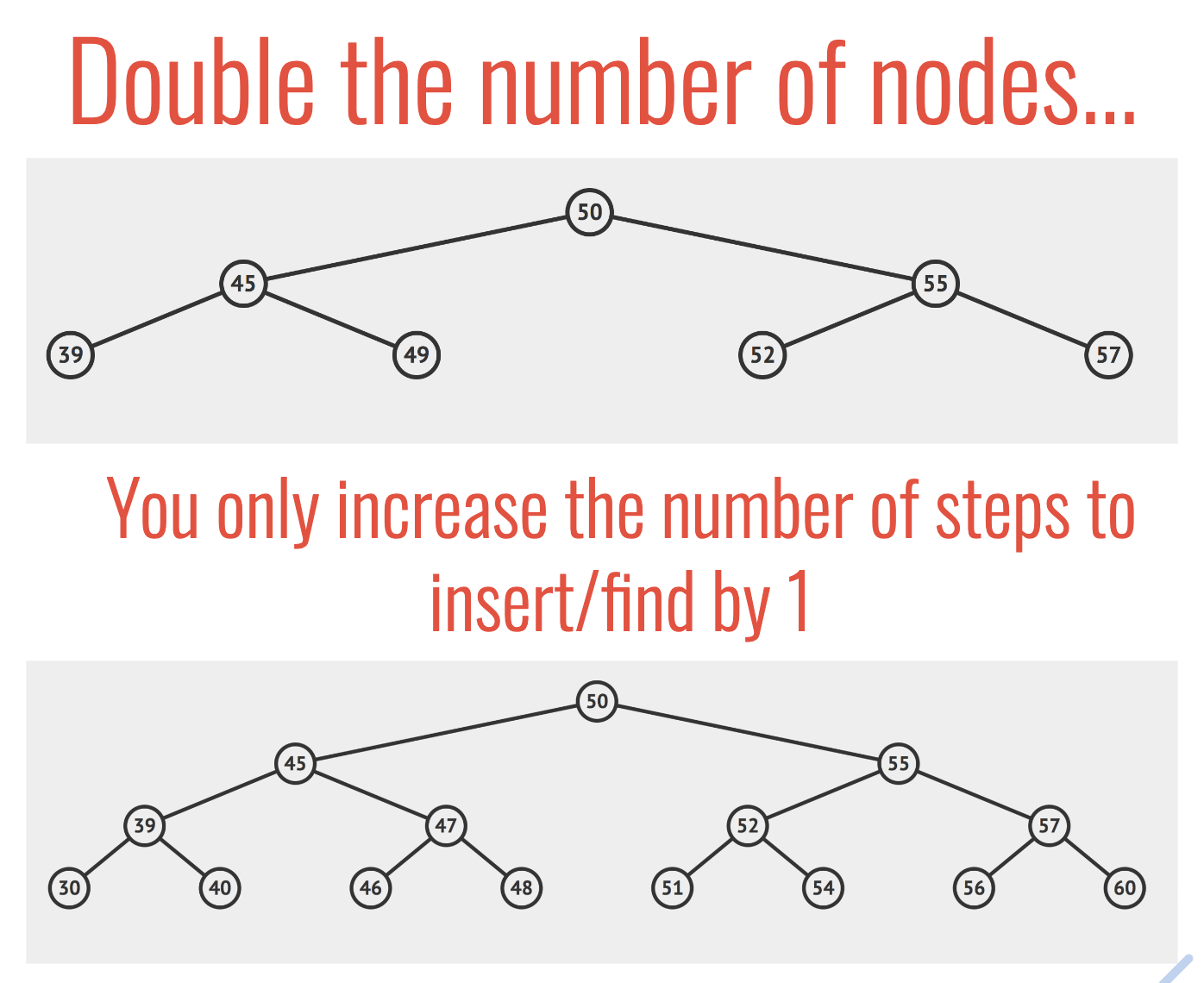
노드 추가와 탐색, 두 경우 모두 잘 정렬되어 있는 경우
O(log n)의 시간복잡도를 가진다. 아래 이미지처럼 노드가 2배 늘어나도 길이 1만큼만 증가하는 것을 볼 수 있다.
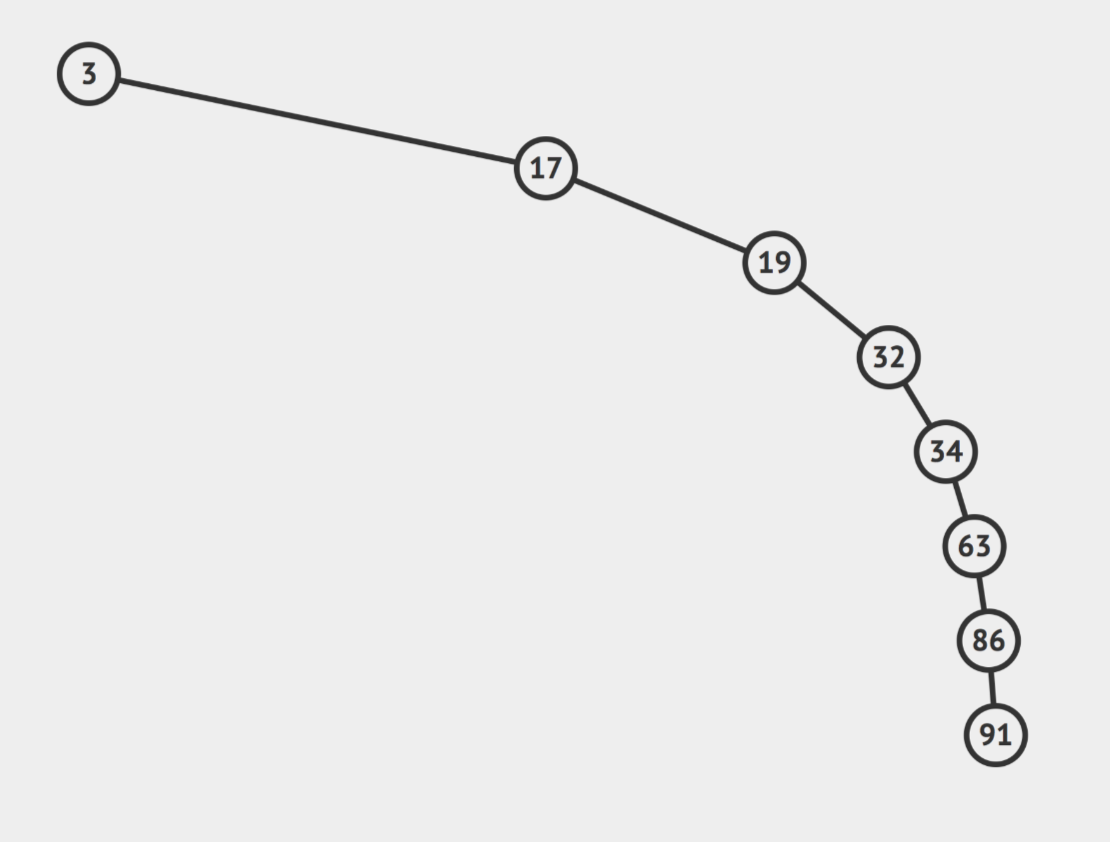
🛑 하지만 장담할 수는 없음!!
한쪽으로 치우쳐진 트리가 있다면 (이것도 유효한 이진 탐색 트리이기 때문에) 최악의 경우 O(n)의 시간복잡도를 가진다.