📆 2022년 9월 22일

n-Queen (DFS, 백트래킹)

일단 너무 만만하게 봤다. DFS인줄도 모르고..
퀸즈갬빗을 재밌게 보고, 체스판만 보고 고른 문제라서

📍 규칙

1. 퀸은 자기가 위치한 행, 열, 대각선으로 움직일 수 있다.
2. 어떤 퀸도 다른 퀸을 잡지 못하도록 배치해야 한다.

즉, n * n 체스보드에 n개의 퀸을 배치하는 문제이다.
(예를 들면, 위 그림(?)은 4-Queen)

n-Queen 역시 코드는 대체적으로 비슷한 것 같다. 이해하는 건 다른 문제 체스 보드에 퀸을 때, 가로, 세로, 대각선에 기물이 있는지 확인하는 방법이 있지만, 먼저 한 행에는 퀸이 1개만 올 수 있다는 가정만 가지고 생각해 본다. 그럼 한 칸의 4가지 경우가 있으므로 4 * 4 * 4 * 4 = 256가지의 경우의 수가 생긴다.

🛑 잠깐! 백트래킹 기법

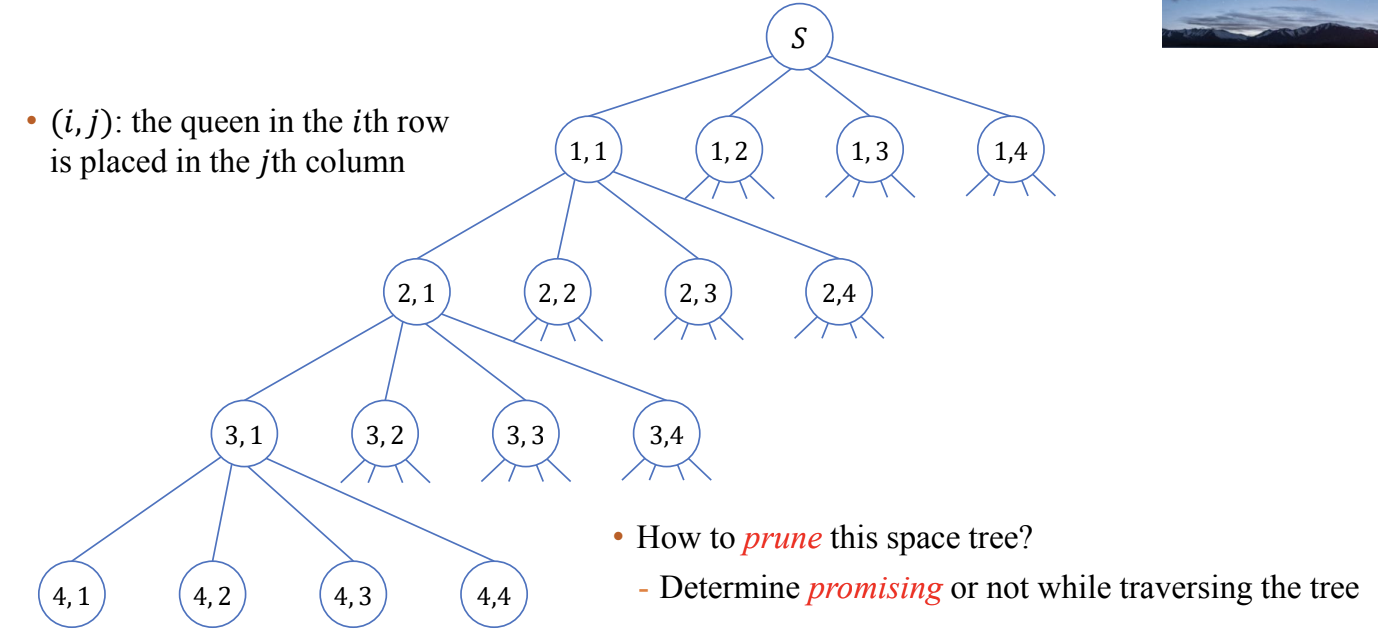
위와 같은 문제 해결을 위해 암묵적으로 작성하는 트리를 상태공간트리라고 한다..고 한다.
꼭 만들어야 하는 것은 아니며, 탐색 공간을 트리 형태의 구조로 암묵적으로 해석이 가능하다고 한다. 내 경우엔 트리 구조로 보니까 좀 더 이해가 잘 되긴 했다.

아무튼 DFS으로 탐색할 때, 모든 노드를 전부 확인하지 않아도 방문 중인 노드에서 하위 트리를 방문하지 않고도 가능성이 전혀 없을 경우가 생길 수 있다.

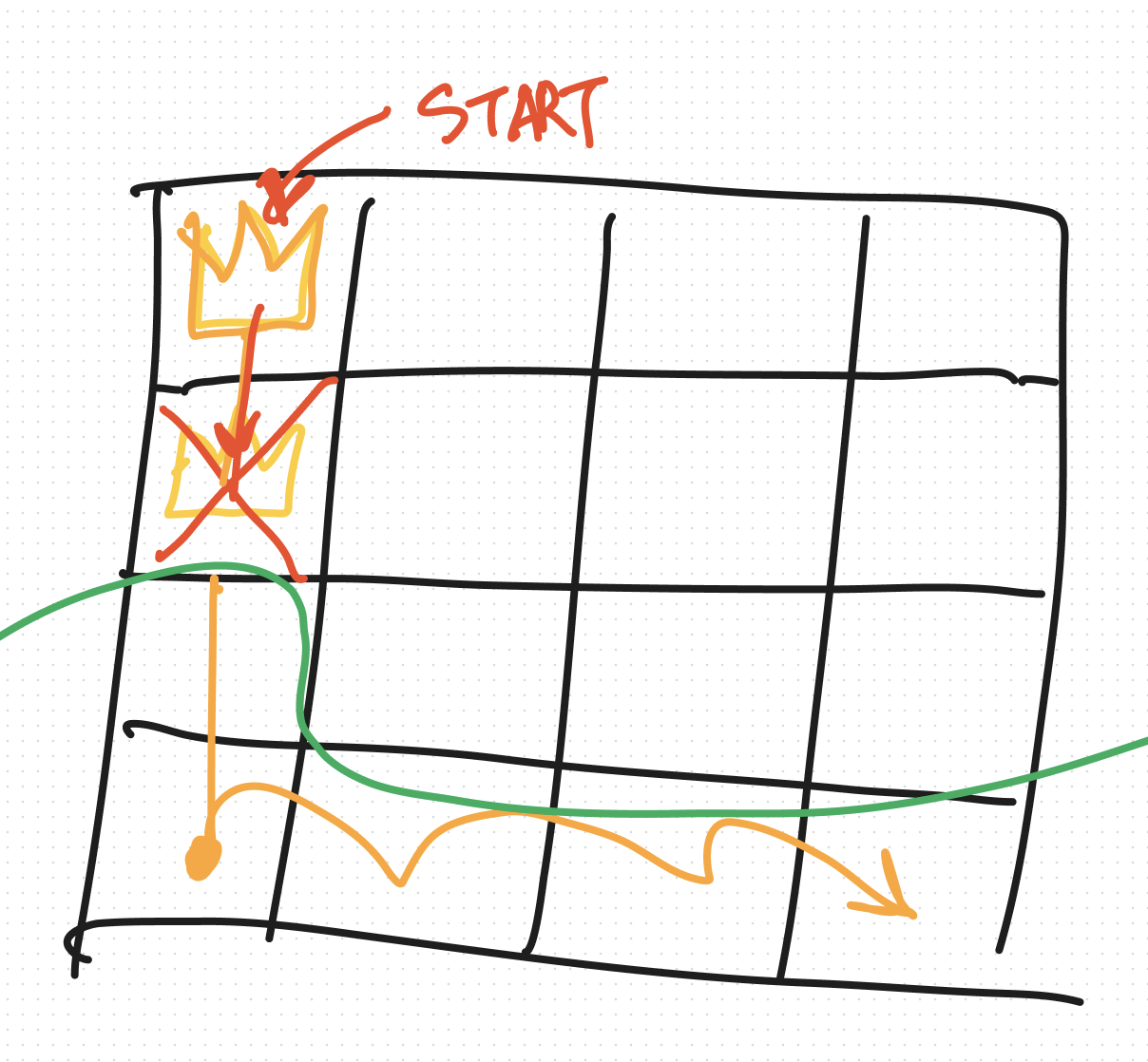
원래는 빨간선에 이어 노란선까지 탐색을 이어가야 하지만, n-Queen 같은 문제는 조건상 결과가 첫번째 행과 두번째 행이 연속해서 오는 케이스는 없기 때문에 초록선 아래로는 탐색하지 않고 다시 1,1로 돌아와 2,2부터 탐색을 진행할 수 있다.

체스판으로 보면 더욱 명확한데, 1,1과 2,1을 가지고 만드는 경우 중에 정답은 없다는 것..

정리하면, 백트래킹과 가지치기는
1. 상태공간트리를 DFS로 탐색하고
2. 방문 중인 노드가 유망한지 체크 후
3. 만약 유망하지 않다면, 백트래킹(부모노드로 돌아감)한다.

---

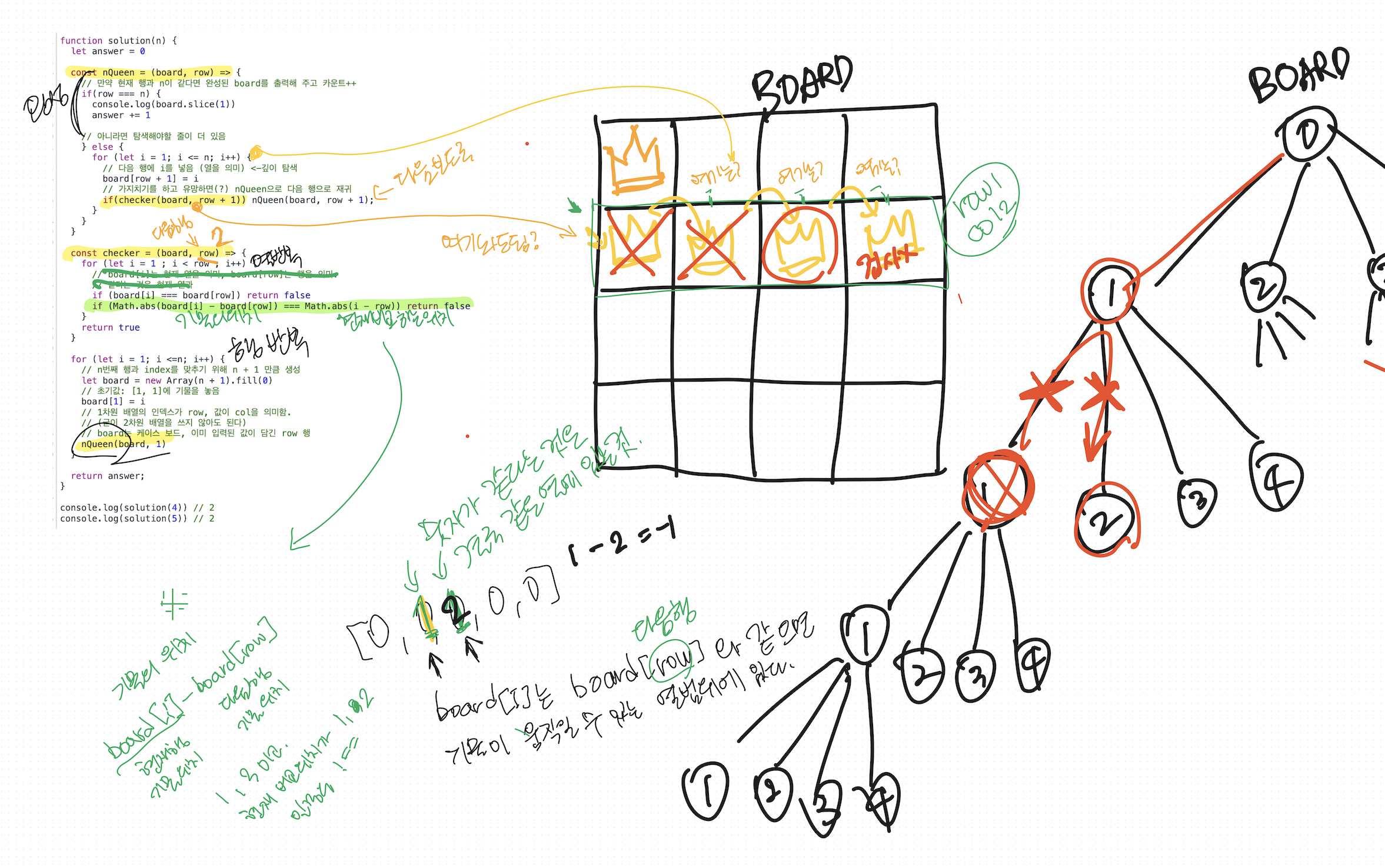
😤 구현 (javascript)

코드를 분석하면서 생각했던 중요한 것은 2가지였다. 첫번째는 1차원 배열로 보드의 기물의 위치를 파악하는 것과 두번째는 백트래킹 조건을 구현하는 것. 강의에서 구현했던 코드를 기준으로 행을 반복하면서 백트래킹 조건으로 같은 열에 있는지, 대각선에 위치하는지를 확인하는데, 좌표 식을 이해하기가 힘들었다.

⚠️ 주석 주의

function solution(n) {
  let answer = 0
  
  const nQueen = (board, row) => {
    // 만약 현재 행과 n이 같다면 완성된 board를 출력해 주고 카운트++
    if(row === n) {
      console.log(board.slice(1))
      answer += 1
      
    // 아니라면 탐색해야할 줄이 더 있음 
    } else {
      for (let i = 1; i <= n; i++) {
        // 다음 행에 i를 넣음 (열을 의미) <-깊이 탐색
        board[row + 1] = i
        
        // 가지치기를 하고 유망하면(?) nQueen으로 다음 행으로 재귀
        if(checker(board, row + 1)) nQueen(board, row + 1);
      }
    }
  }

  const checker = (board, row) => {
    for (let i = 1 ; i < row ; i++) {
      // board[i]는 현재행을 의미, board[row]는 다음행을 의미. 
      // 같다는 것은 현재행(기물의 위치)와 다음에 놓을 기물의 위치를 계산함. 
      // 행은 이미 조건으로 했으니, 같은 열에 있는지, 대각선으로 있는지만 검사.
      if (board[i] === board[row]) return false
      if (Math.abs(board[i] - board[row]) === Math.abs(i - row)) return false
    }
    return true
  }

  for (let i = 1; i <=n; i++) {
    // n번째 행과 index를 맞추기 위해 n + 1 만큼 생성
    let board = new Array(n + 1).fill(0)
    // 초기값: [1, 1]에 기물을 놓음
    // 1번행의 열을 반복함 1~4
    board[1] = i
    // 1차원 배열의 인덱스가 row, 값이 col을 의미함.
    // (굳이 2차원 배열을 쓰지 않아도 된다)
    // board는 케이스 보드, 이미 입력된 값이 담긴 row 행
    nQueen(board, 1)
  }
  
  return answer;
}

console.log(solution(4)) // 2
// console.log(solution(8)) // 2

구현 (python)

파이썬 코드는 아래 n-Queens 문제의 구현에서 가져왔습니다.

def n_queens (i, col):
    n = len(col) - 1
    if (promising(col, i)):
        if (i == n):
            print(col[1: n + 1])
        else:
            for j in range(1, n + 1):
                col[i + 1] = j
                n_queens(col, i + 1)

def promising (i, col):
    k = 1
    flag = True
    while (k < i and flag):
        if (col[i] == col[k] or abs(col[i] - col[k]) == (i - k)):
            flag = False
        k += 1
    return flag

n = 8
col = [0] * (n + 1)
n_queens(0, col)

---

🤔 문제

성능 최적화에 대한 부분이 약간 걱정이 된다.
프로그래머스는 어찌 통과가 되었는데, 백준은 어떨지.

• ✅ N-Queen | 프로그래머스
• N-Queen | boj

---

약간은 DFS와 친해(?)진 것 같은 기분이 들고 막 풀 수 있을 것 같고!! 🥹

출처

파이썬으로 배우는 알고리즘 기초: 19. n-Queens 문제의 구현 | youtube
파이썬으로 배우는 알고리즘 기초: 18. 백트래킹과 n-Queens 문제 | youtube
프로그래머스 LV.3 N-Queen (JS) | @longroadhome
여덟 퀸 문제 | 나무위키