1. 트리

1.1 개념

• 계층이 존재하는 비선형 자료구조
• 나무를 거꾸로 뒤집어 놓은 듯한 모습임
• 그림
  

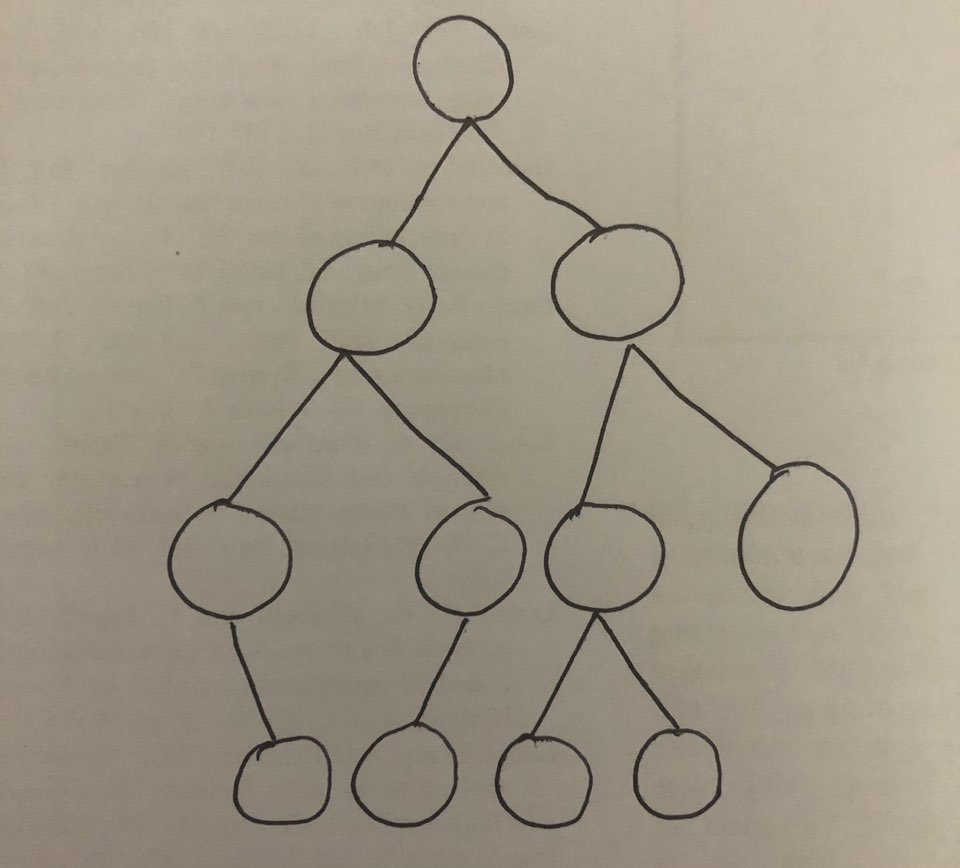
1.2 용어

1.2.1 그림

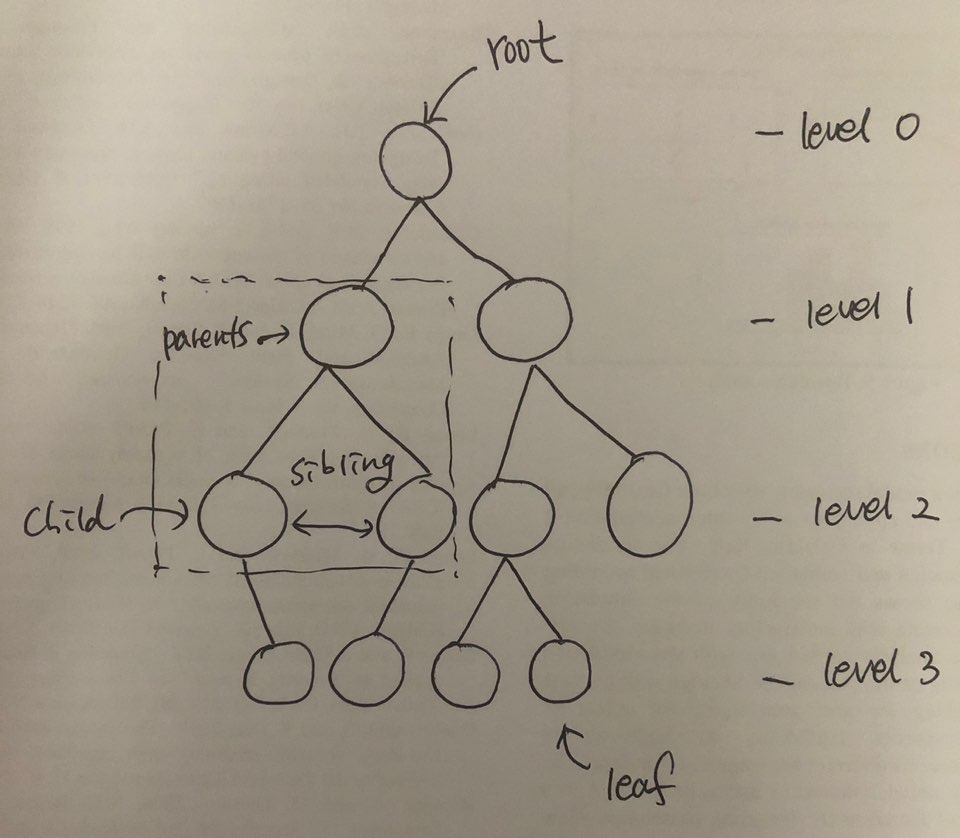
1.2.2 용어 설명

• node: 데이터를 저장하는 기본요소
• root node: 트리의 level0 에 존재하는 노드
• level: 트리의 깊이를 나타내는 단위
• parent node: 어떤 노드의 상위에 연결된 노드
• child node: 어떤 노드의 하위에 연결된 노드
• sibling: 동일한 level에 존재하는 노드
• depth: 노드가 가질 수 있는 최대 깊이(level)
• leaf node: child node가 없는 노드

1.3 종류

• 이진 트리, 이진 탐색 트리, 균형 트리, 이진 힙 등

2. 이진 트리

2.1 개념

• 각 노드의 child node의 개수가 최대 2개인 트리
• 각 노드의 child node의 개수는 0개, 1개 또는 2개

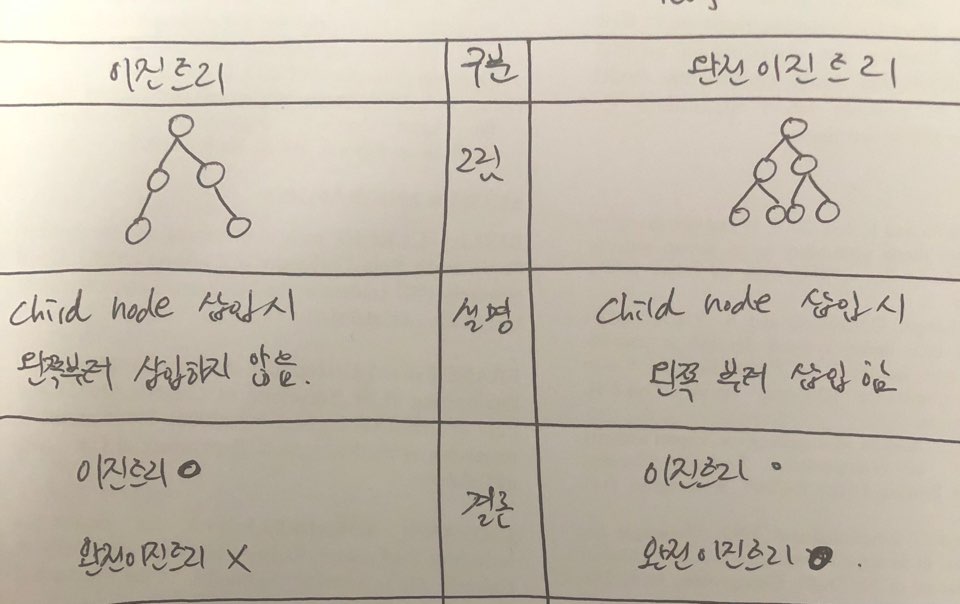
2.2 이진트리와 완전이진트리

2.3 표현하기

2.3.1 트리(tree)를 리스트(list)형식으로

-아래와 같은 트리구조가 있을 때 표현 방법은 다음과 같다.

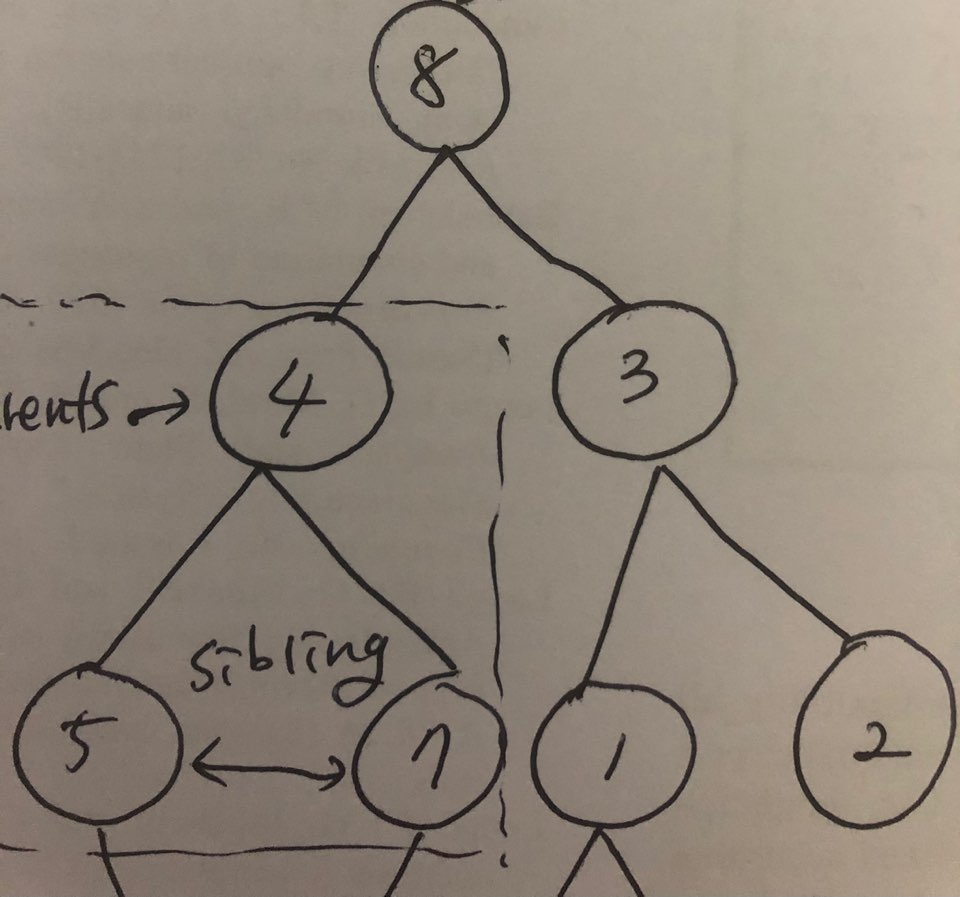
• 리스트 표현: [None, 8, 4, 3, 5, 7, 1, 2]

2.3.2 리스트(list)를 트리(tree)형식으로

• 공식을 이용하면 어떤 구조인지 도식화가 가능하다
• 공식:
  ㅇ child 왼쪽 노드: index 2
  ㅇ child 오른쪽 노드: index 2 + 1
  ㅇ parent 노드: index // 2
• 예시
  ㅇ 리스트 표현: [None, 8, 4, 3, 5, 7, 1, 2]
  ㅇ root 노드: 8
  ㅇ root 노드의 왼쪽 child 노드: 4 (=1x2 번째 노드)
  ㅇ index가 3인 노드의 오른쪽 child 노드: 2 (=3x2+1 번째 노드)
  ㅇ index가 3인 노드의 parent 노드: 8 (=3 //2 = 1 번째 노드)

2.4 특징

• 한 level 노드 개수: 2^level depth 개
• 전체 노드의 최대 개수(N): 2^h - 1
• 최대 이진 트리의 높이: O(log(N))