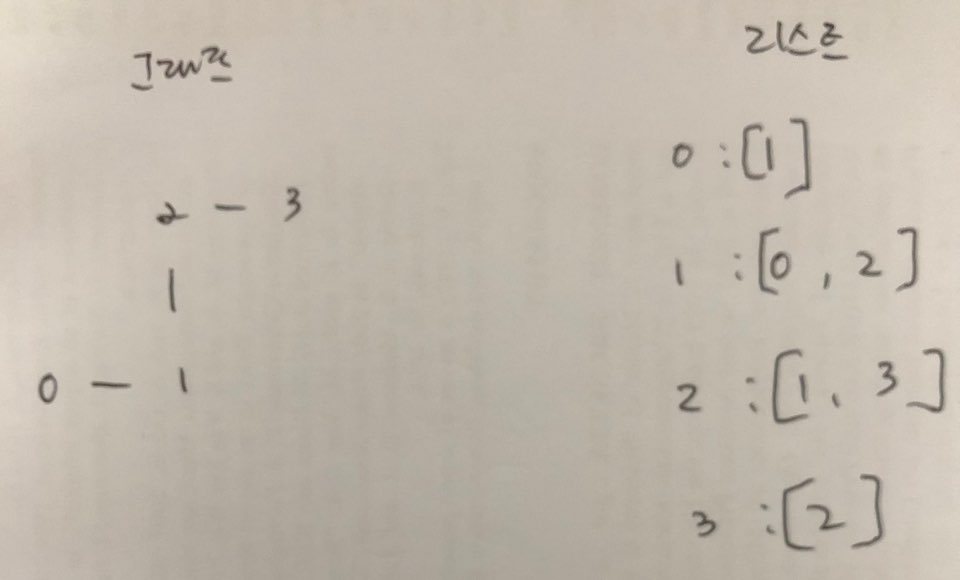1. 힙

1.1 개념

• 최댓값이 루트 노드(root node)에 위치한 완전이진트리(complete binary tree)

1.2 특징

• 부모 노드의 크기는 자식 노드의 크기보다 큼
• 예시
  
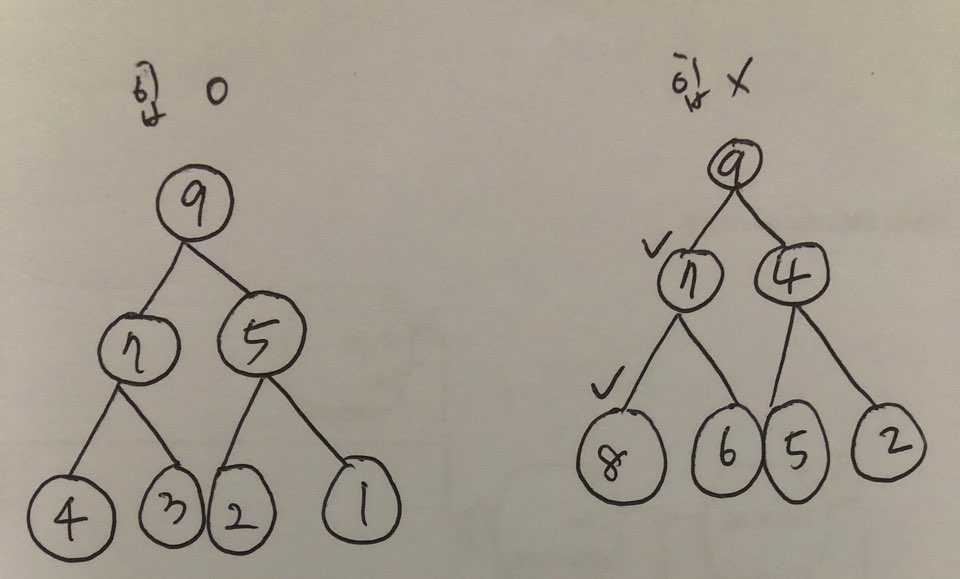
  ㅇ 오른쪽 이진트리는 힙이 아님(7과 8, 4와 5의 위치 때문)

1.3 추가

1.3.1 구현 개념

• 추가하고자 하는 수를 리스트 가장 마지막에 추가하고, 부모 노드와 비교하여 위치를 변경한다.

1.3.2 예시

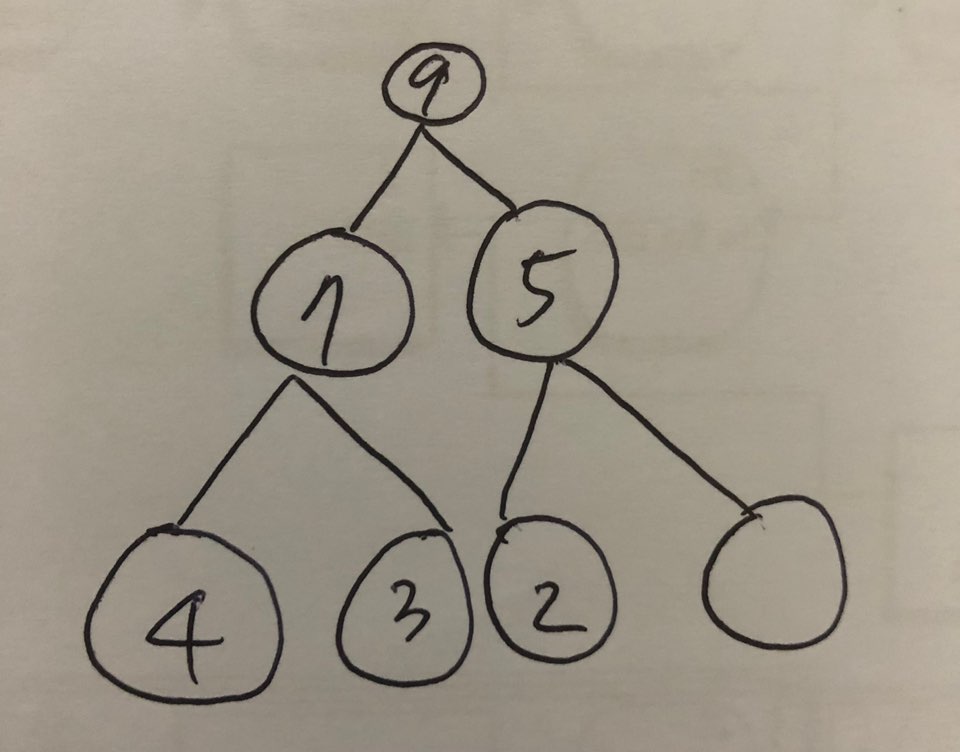
1.3.2.1 추가 전

• 이진트리구성: [None, 9, 7, 5, 4, 3, 2]
• 도식화
  

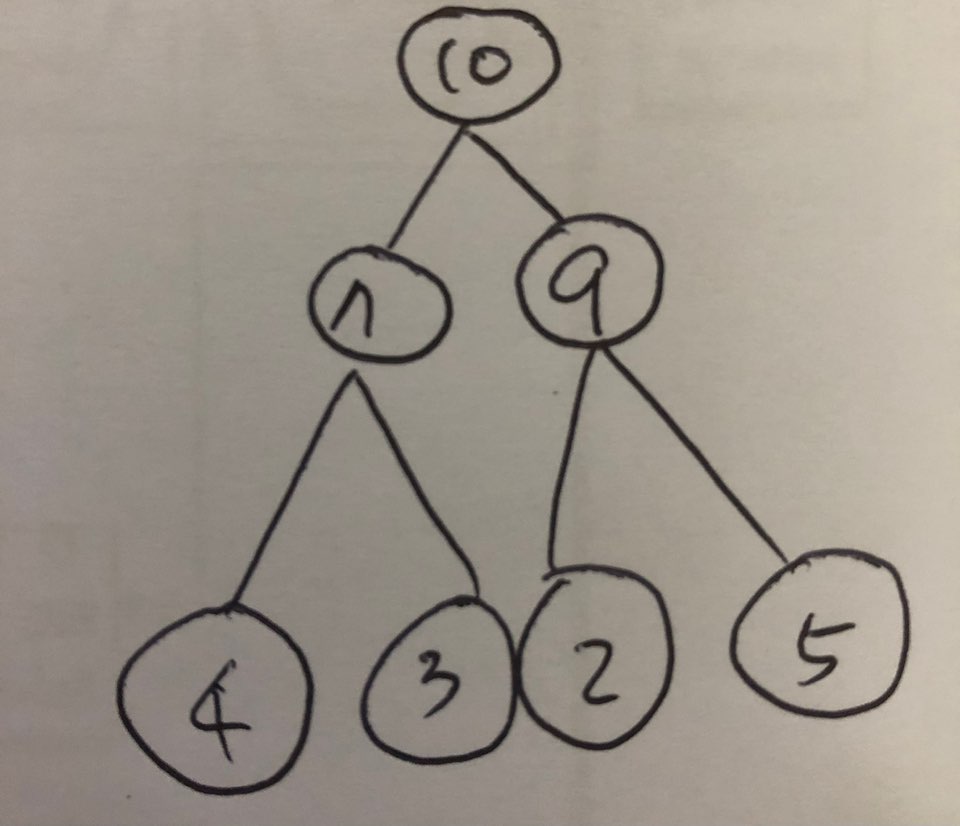
1.3.2.2 추가 후

• 이진트리구성: [None, 10, 7, 9, 4, 3, 2, 5]
• 도식화
  

1.3.2.3 추가 방법

• 그림으로 보기
  
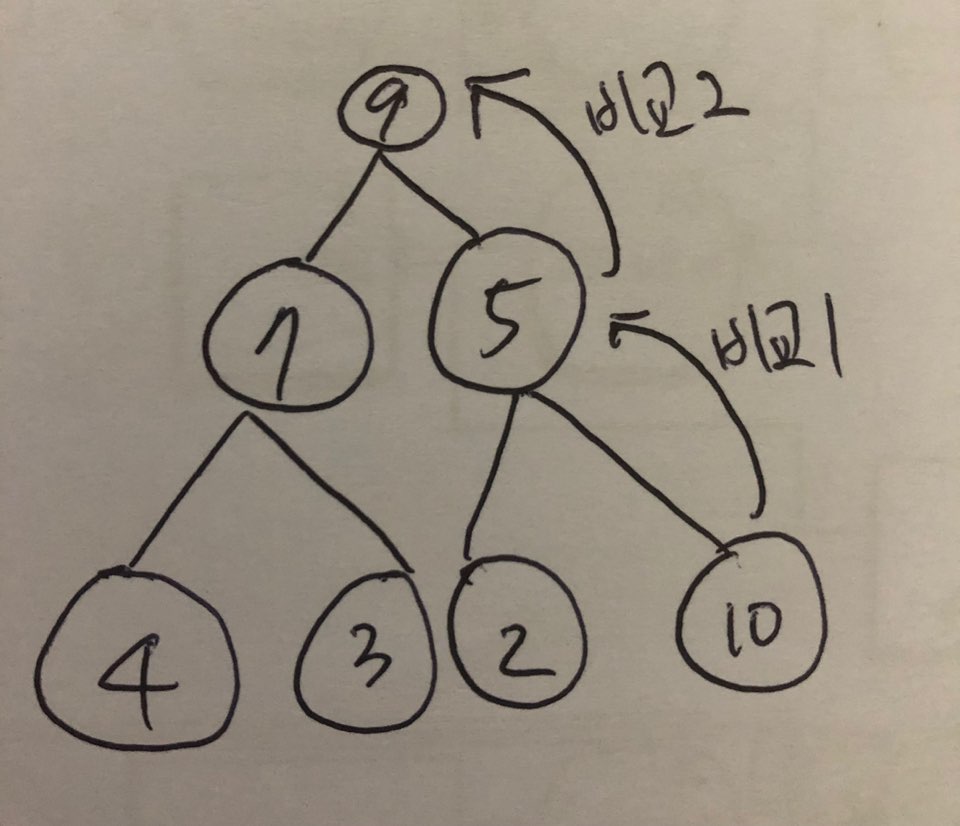
• 코드로 보기

    def insert(self, value):
        
        self.items.append(value) 				  # 1. 마지막에 노드를 추가한다.
        cur_index = len(self.items) - 1
        while cur_index > 1:
            parent_index = cur_index // 2 			  # 2. parent 노드 index 구하기
            if self.items[cur_index] > self.items[parent_index]:  # 3-1. parent 노드와 비교해서 자식 노드가 더 크면
                self.items[parent_index], self.items[cur_index] = self.items[cur_index], self.items[parent_index] # 3-2. child 노드와 parent 노드의 자리를 변경한다.
                cur_index = parent_index
            else:
                break

1.4 삭제

1.4.1 구현개념

• 최댓값을 삭제하고 싶다면, 최댓값과 가장 마지막 노드의 자리를 변경하고, 최댓값을 삭제한다.
• 힙의 특성을 유지하기 위해 변경된 루트 노드 숫자의 위치는 변경한다.

1.4.2 예시

1.3.2.1 삭제 전

• 이진트리구성: [None, 9, 7, 5, 4, 3, 2, 1]
• 도식화
  

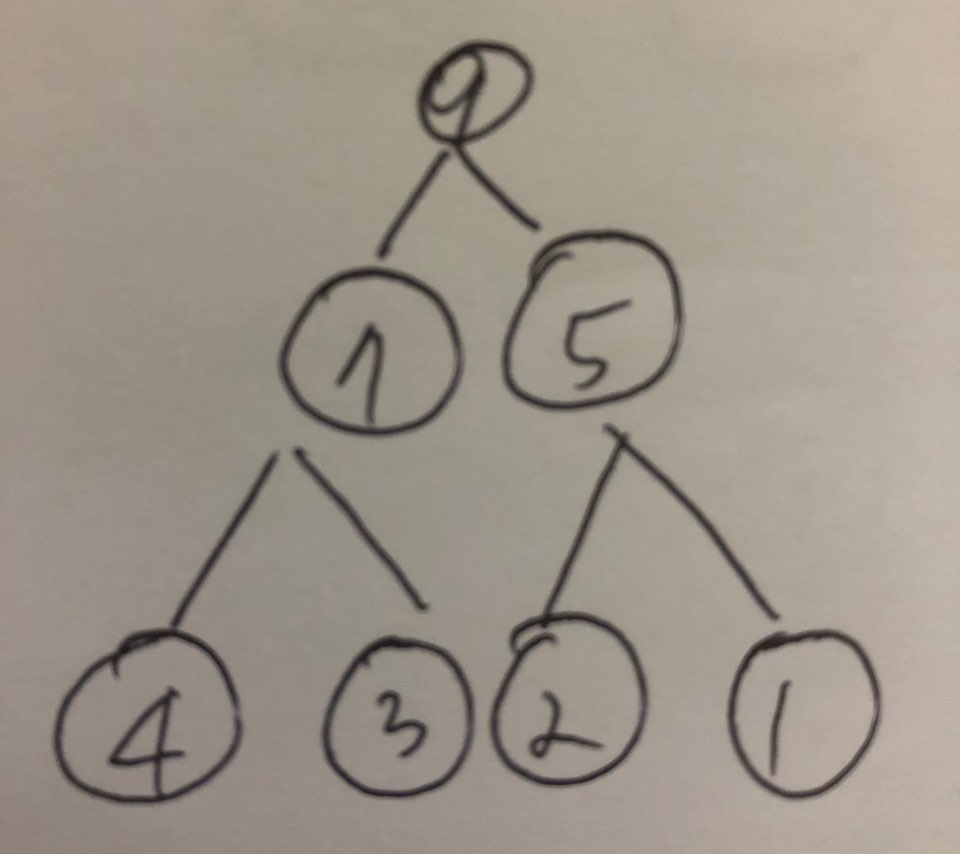
1.3.2.2 삭제 후

• 이진트리구성: [None, 7, 4, 5, 1, 3, 2]
• 도식화
  

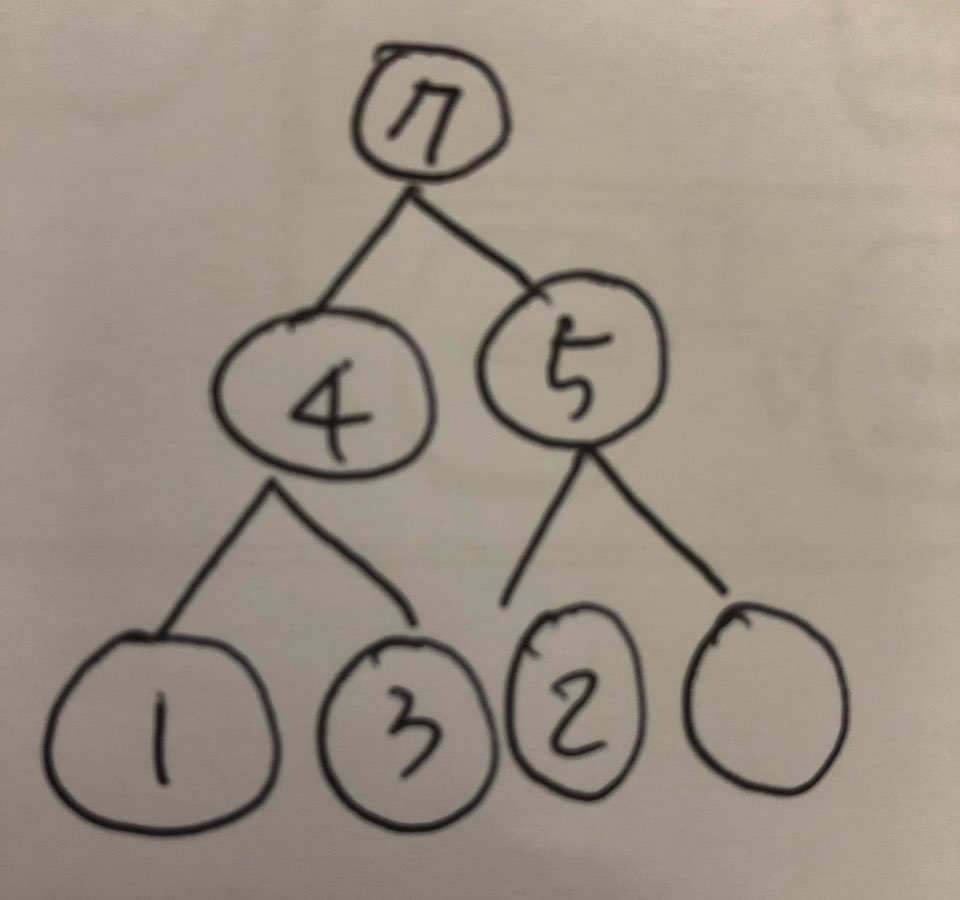
1.3.2.3 삭제 방법

• 그림으로 보기
  
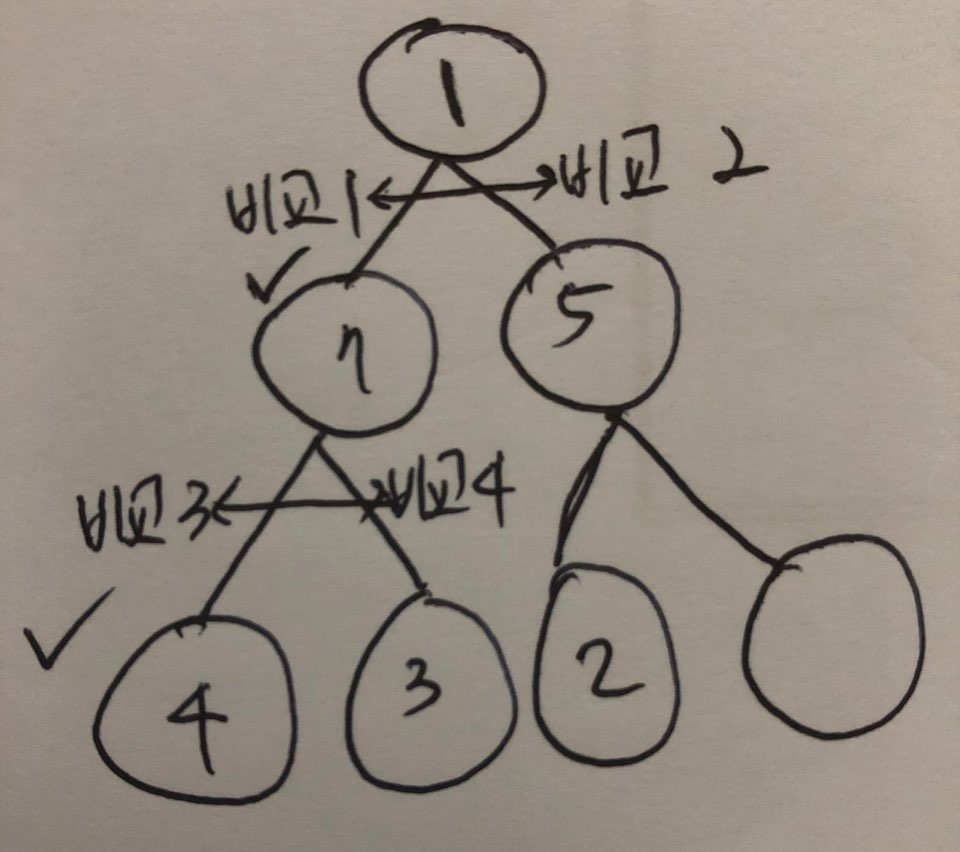
• 코드로 보기

    def delete(self):
    
        self.items[1], self.items[-1] = self.items[-1], self.items[1] 			   					      #1.자리 변경: 루트 노드와 마지막 노드의 자리를 변경한다.

        prev_max = self.items.pop() 												      #2.노드 삭제: 변경된 마지막 노드(9)를 빼낸다.
        cur_index = 1 														      #3.index선언: 움직일 노드의 index를 선언한다.

        while cur_index < len(self.items) - 1: 											      #4~11번 과정을 현재 index가 list의 길이보다 작을 때까지 반복한다.
            left_node_index = cur_index * 2  											      #4.index선언: child 노드 왼편 index 선언한다.
            right_node_index = cur_index * 2 + 1 										      #5.index선언: child 노드 오른편 index 선언한다.
            if self.items[right_node_index] < self.items[left_node_index] and self.items[left_node_index] > self.items[cur_index]:    #6. 노드 비교: child의 왼쪽 노드와 오른쪽 노드를 비교해서 왼쪽이 크고, 왼쪽과 현재 노드의 크기를 비교해 현재 노드가 작으면
                self.items[cur_index], self.items[left_node_index] = self.items[left_node_index], self.items[cur_index] 	      #7.자리 바꾸기: child 왼쪽 노드와 현재 노드의 자리를 바꾼다.
                cur_index = left_node_index 											      #8.index 재설정: 현재 노드의 위치를 재설정한다.
            elif self.items[right_node_index] > self.items[left_node_index] and self.items[right_node_index] > self.items[cur_index]: #9. 노드 비교: child의 왼쪽 노드와 오른쪽 노드를 비교해서 오른쪽이 크고, 오른쪽과 현재 노드의 크기를 비교해 현재 노드가 작으면
                self.items[cur_index], self.items[right_node_index] = self.items[right_node_index], self.items[cur_index] 	      #10.자리 바꾸기: child 오른쪽 노드와 현재 노드의 자리를 바꾼다.
                cur_index = right_node_index 											      #11.index 재설정: 현재 노드의 위치를 재설정한다.

        
        return prev_max

2. 그래프

2.1 개념

• 연결되어 있는 정점와 정점간의 관계를 표현할 수 있는 자료구조. [천재학습백과]

2.2 용어

• 노드(node): 데이터를 가진 한 지점
• 간선(Edge): 노드와 노드를 연결하는 선
• 인접노드(adjacent node): 한 노드에 대하여 간선으로 이어진 노드

2.3 표현법

2.3.1 행렬

• 그래프 및 행렬 표시
  
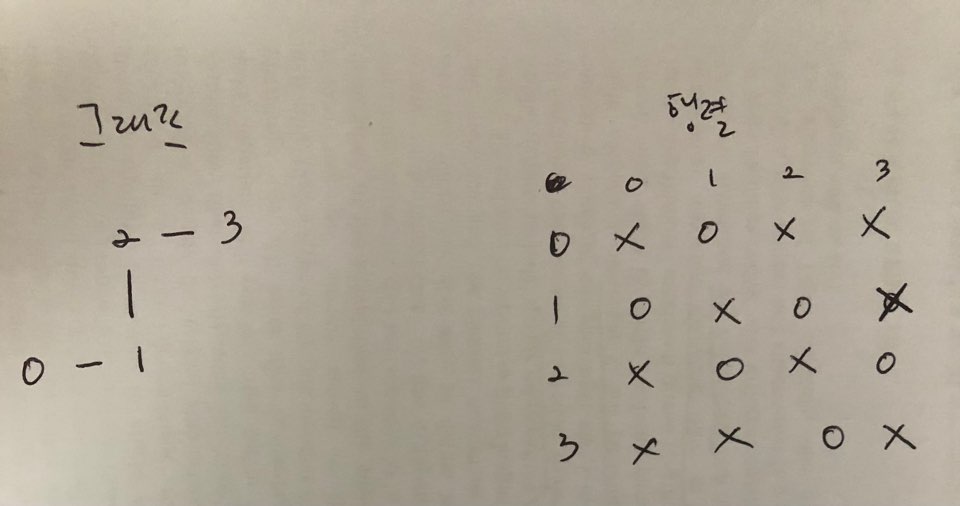
• 특징
  ㅇ (리스트 대비) 공간 복잡도 증가, 시간 복잡도 감소

2.3.2 리스트

• 그래프 및 리스트 표시
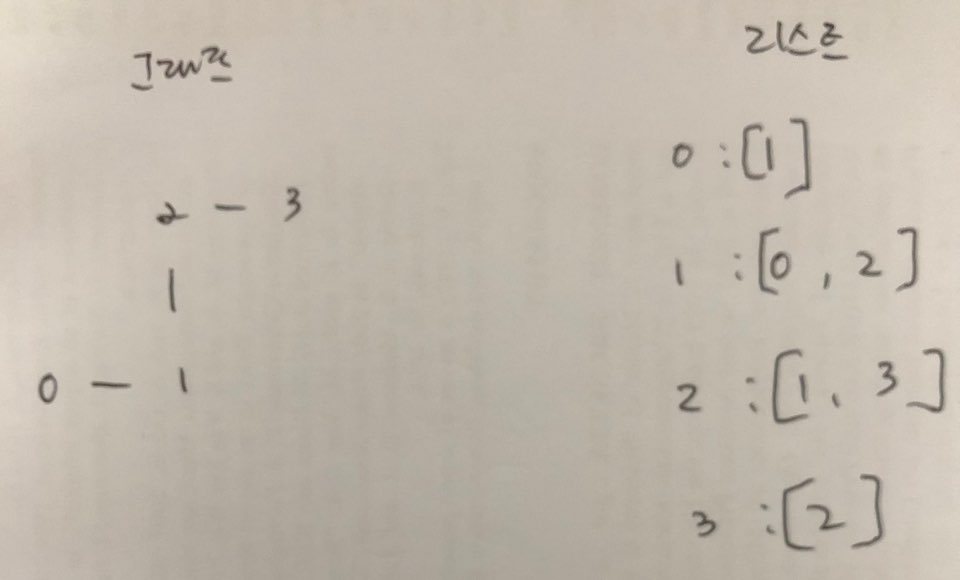
• 특징
  ㅇ (행렬 대비) 공간 복잡도 감소, 시간 복잡도 증가