해시테이블, 힙, 트리
1. 자료구조 알고리즘 2주차 강의
1-1 해시테이블
:평균 시간 복잡도가 O(1)이다 -> 빠르다 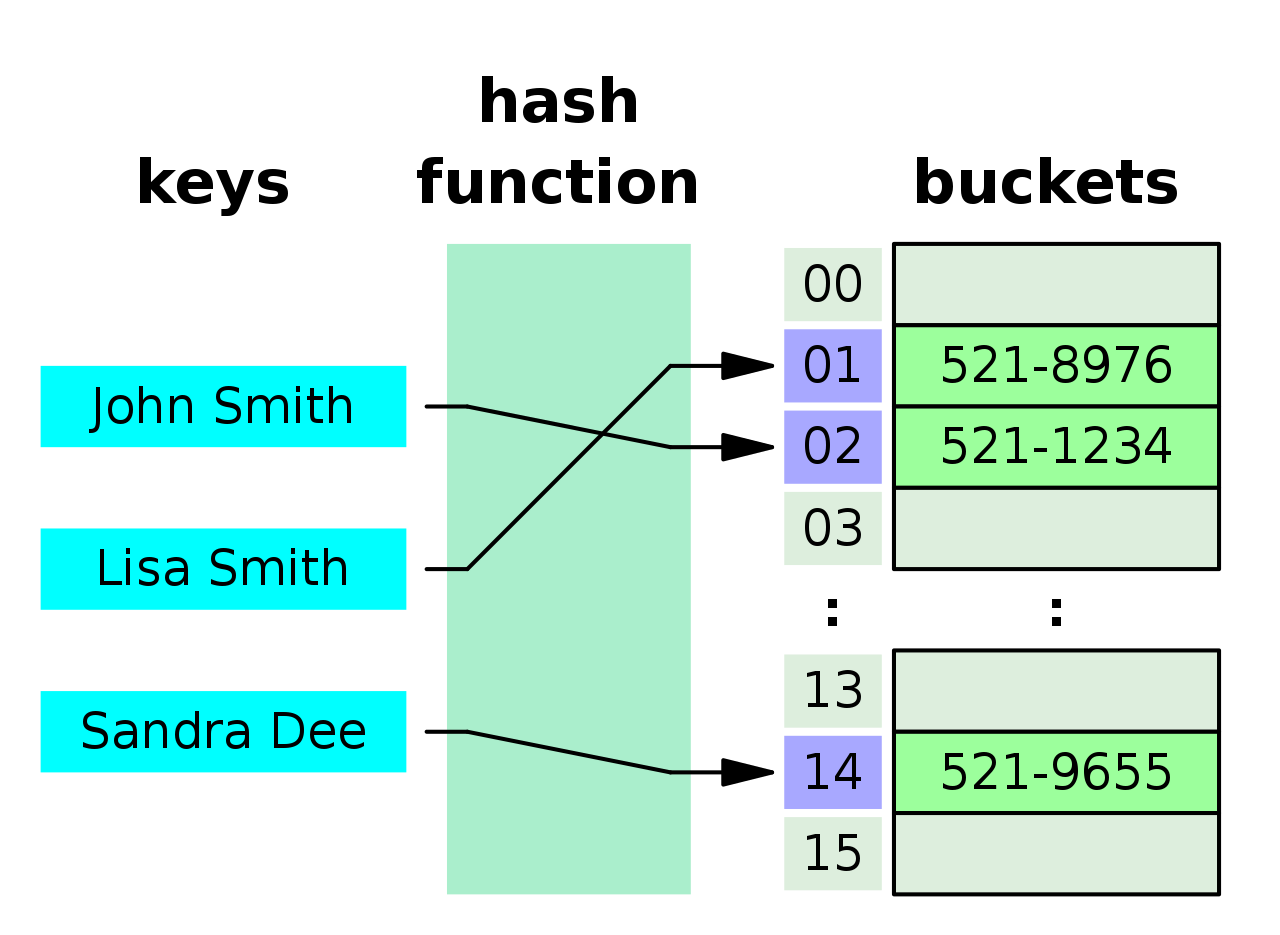
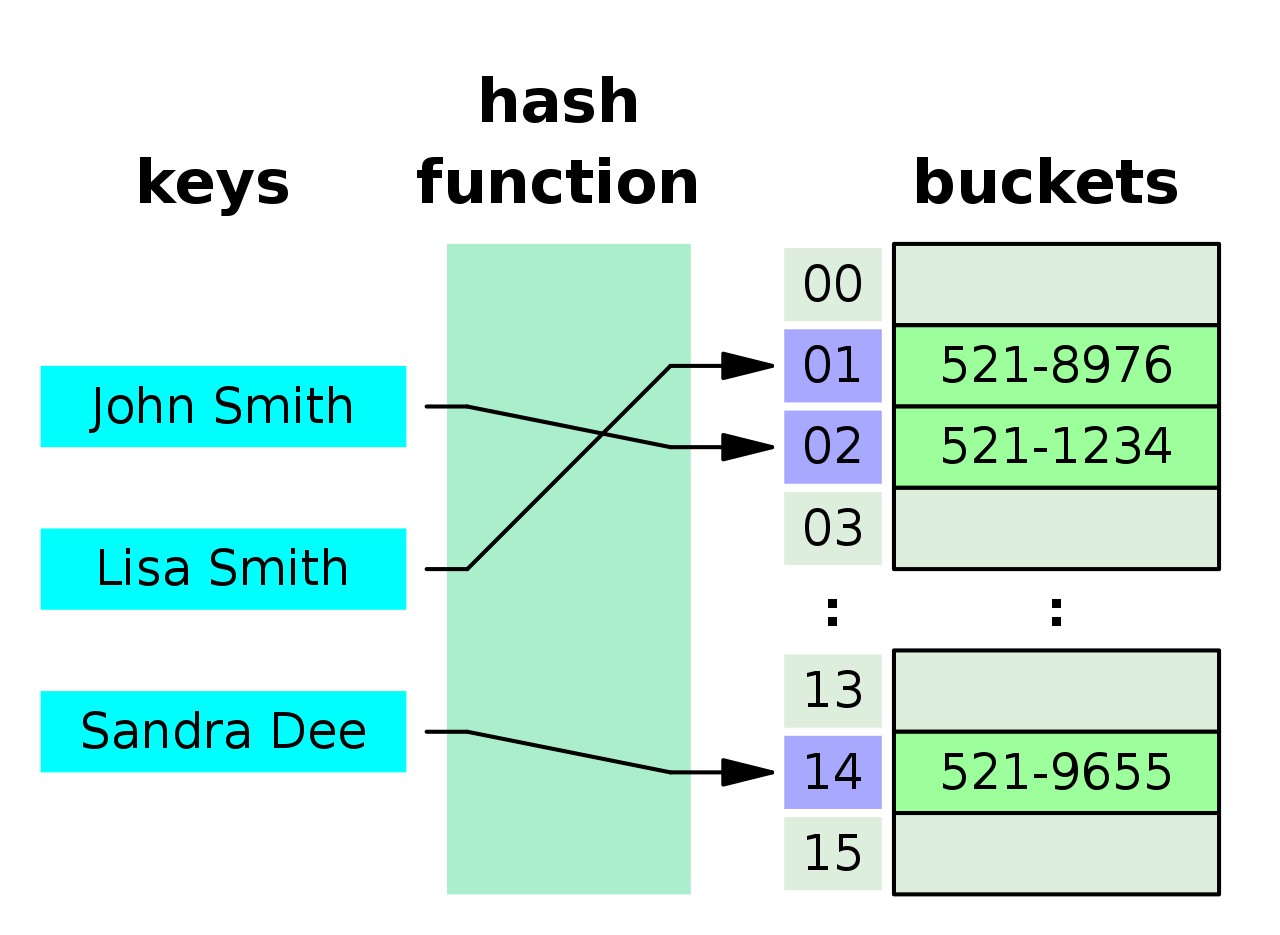
1-1-1 해시함수
key를 어떠한 고정크기의 값으로 변환시켜주는 함수
예) John Smith -> 02로 변환
1-1-2 해시함수의 성능
해시 값이 충돌의 가능성이 적어야함
쉽고 빠른 연산 = 적은 시간
해시테이블 사용효율이 높음 = 작은 공간(데이터)
해시값들의 균등한 분포
모든 key에 대해 해싱(매핑)이 되어야 함
💡 많이 사용하는 정수형 해싱 기법
h(key) = key mod M (M = 2의 멱수에서 먼 소수)
1-1-3 로드 팩터
Load factor = n / k (n=데이터 개수 k = 버킷 개수)
보통 값이 증가할수록 해시테이블의 성능이 감소
자바 10 => 0.75 이상이 될시 해시테이블 공간 재할당
💡 시간과 공간 비용의 적절한 절충안을 찾는 과정이 필요
==> 실험적으로 알아가야 한다
1-1-4 개별 체이닝
충돌 발생시 연결리스트로 연결
=> 최악의 경우 O(N)
1-1-5 오픈 어드레싱
충돌시 해시테이블 공간을 탐사 -> 빈공간 찾기
=> h(key) != 저장한 곳의 해시값
=> 뭉쳐서 저장되는 경우가 많다
💡 선형탐사 => 파이썬의 방식
아래 표처럼 Load factor값이 임계값을 넘어가면
해시테이블을 늘린다 => 평균적으로 체이닝보다 효율이 좋다 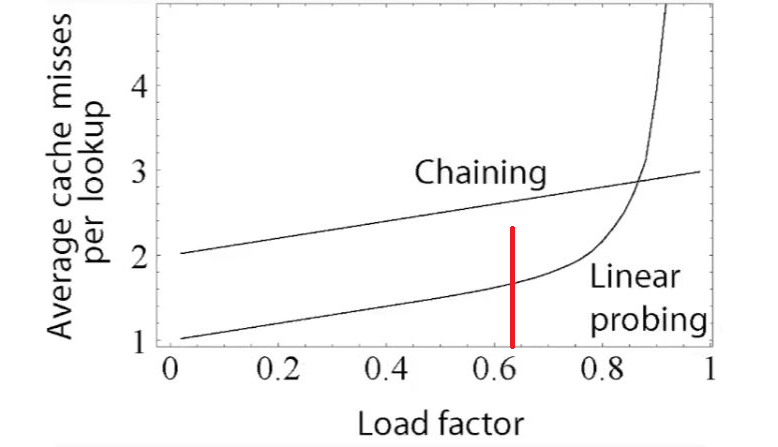
1-2 Heap
: 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리 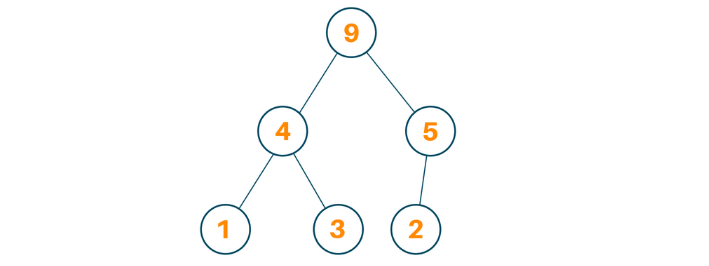
1-2-1 이진트리
: 각각의 노드가 최대 두 개의 자식 노드를 가지는 구조
<완전이진트리>
-> 마지막 레벨을 제외, 모든 레벨이 완전히 채워져 있다
-> 마지막 레벨의 모든 노드는 가장 왼쪽에 있다.
1-2-2 heap
Max heap: 항상 가장 큰 값이 상위레벨에 있도록 하는 구조 O(log(N))
Min heap: 항상 가장 작은 값이 상위레벨에 있도록 하는 구조
💡1) 이진탐색트리(BST)와 다르게 자식의 위치가 대소관계를 반영하지 않음
2) 보통 계산 편의를 위해 인덱스는 1부터 사용한다
(parent: x, left: 2x, right: 2x+1)
1-2-3 Maxheap code
삽입 알고리즘
1. 원소를 맨 마지막에 넣습니다.
2. 그리고 부모 노드와 비교합니다. 만약 더 크다면 자리를 바꿉니다.
3. 부모 노드보다 작거나 가장 위에 도달하지 않을 때까지
2과정을 반복합니다.
추출 알고리즘(추출 = 노드를 빼오는 것)
1. 루트 노드와 맨 끝에 있는 원소를 교체한다.
2. 맨 뒤에 있는 원소를 (원래 루트 노드)를 삭제한다.
3. 변경된 노드와 자식 노드들을 비교합니다. 두 자식 중 더 큰 자식과 비교해서
자신보다 자식이 더 크다면 자리를 바꿉니다.
4. 자식 노드 둘 보다 부모 노드가 크거나 가장 바닥에 도달하지 않을 때까지
3과정을 반복합니다.
5. 2에서 제거한 원래 루트 노드를 반환합니다.
문제풀이
2-1 1874. 스택 수열
스택을 활용
1. 숫자 한개를 받았을 때 pop은 한번만 해야함
2. push는 여러번 가능
주어지는 숫자 배열 = l
x번째 숫자 = l(x)
max = 스택에 들어갔었던 가장 높은 수
l(x) >= max -> 스택에 l(x)까지만큼 넣기
l(x) < max -> 무조건 pop을 해야함. 이때, l(x) = pop()
2-2 9012. 괄호, 4949. 균형잡힌 세상
1. 스택에 여는 괄호 {([ 를 오는 순서에 맞춰 넣는다.
2. })]가 올때 스택에서 pop을하여 비교 ==> 짝이 안맞으면 VPS가 아님
3. 끝났을 때 스택에 무엇인가 남아 있으면 VPS가 아님
VPS: 호의 모양이 바르게 구성된 문자열을 올바른 괄호 문자열