Tree, DFS, BFS, 백트래킹
1. 자료구조 알고리즘 2주차 강의
1-1 Tree
:연결되어 있는 정점와 정점간의 관계를 표현할 수 있는 자료구조
1-1-1 용어
노드(Node): 연결 관계를 가진 각 데이터를 의미(정점, Vertex)
간선(Edge): 노드 간의 관계를 표시한 선
인접 노드(Adjacent Node): 간선으로 직접 연결된 노드
1-1-2 종류
유방향 그래프(Directed Graph): 방향이 있는 간선을 가짐
무방향 그래프(Undirected Graph): 방향이 없는 간선을 가짐
1-1-3 표현
인접 행렬(Adjacency Matrix): 2차원 배열로 그래프의 연결 관계를 표현
인접 리스트(Adjacnecy List): 링크드 리스트로 그래프의 연결 관계를 표현
💡 차이점: 시간 VS 공간
인접 행렬: 즉각적으로 연결되었는지 여부를 바로 알 수 있다.
하지만 O(node²)의 공간이 필요함.
인접 리스트: 즉각적으로 연결되었는지 알 수 없다. O(edge)
대신 모든 조합의 연결 여부를 저장할 필요가 없다.
따라서 O(node+edge)만큼의 공간을 사용. 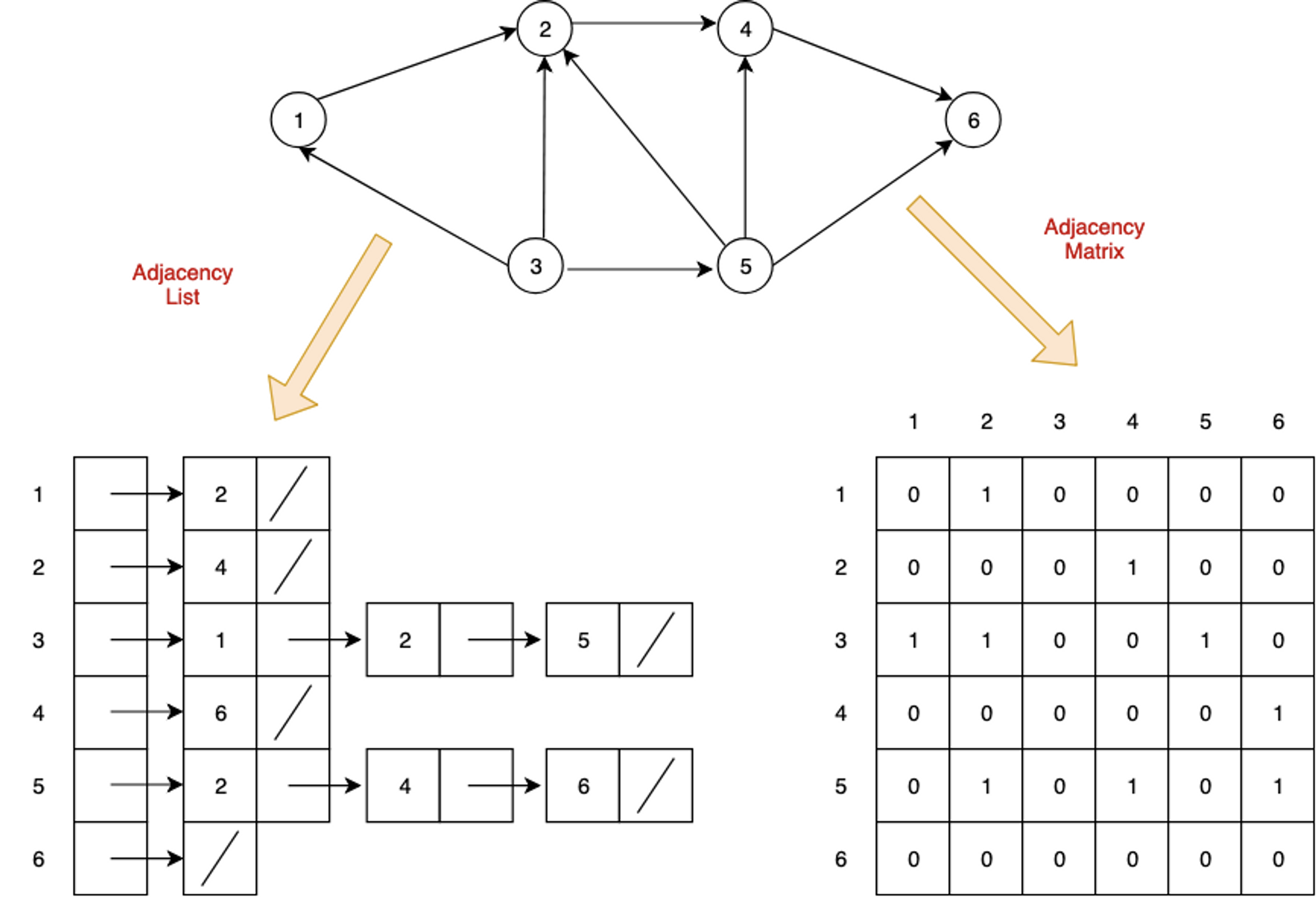
1-2 DFS
:Depth First Search 깊이 우선 탐색
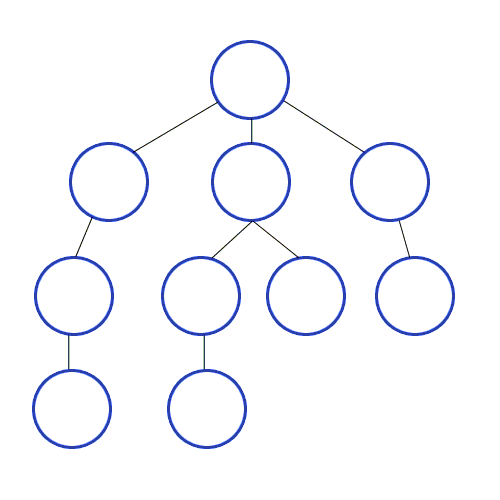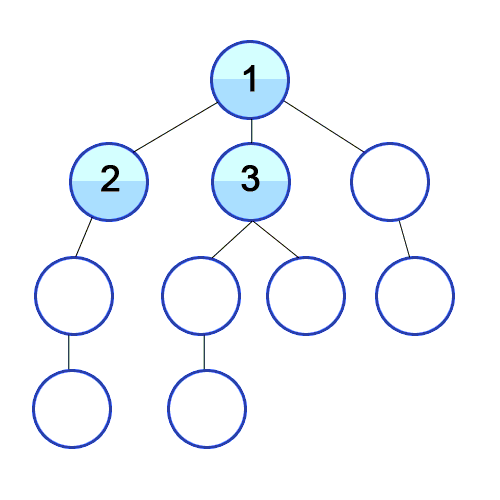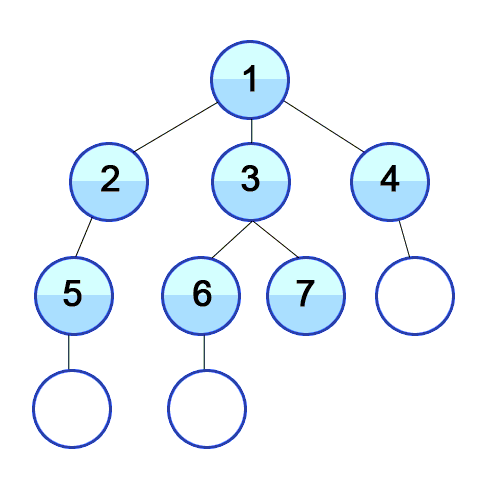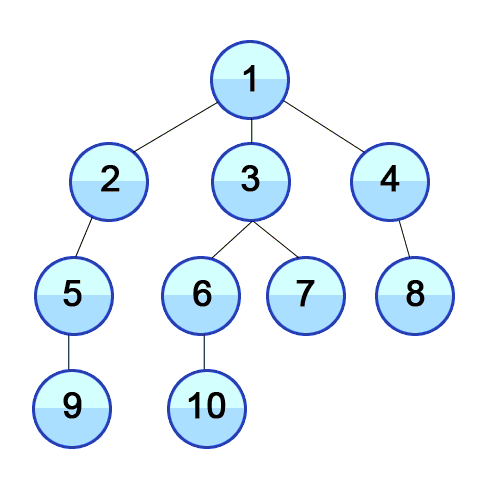
1-2-1 탐사(구현) 방법
1. 갈 수 있는 노드가 있다면 계속해서 탐색
2. 갈 수 있는 노드가 없다(= 갔던 곳 밖에 없다)
=> 전 노드(부모)로 이동(스택 활용)
3. 1-2를 반복
1-3 BFS
:Breadth First Search 너비 우선 탐색
1-3-1 탐사(구현) 방법
1. 루트 노드를 큐에 넣는다
2. 큐에서 노드를 빼서 visited 에 추가한다.
3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 큐에 추가
4. 2, 3 반복
5. 큐가 비면 탐색 종료
1-3 백트레킹
:필요없는 부분을 가지치기(pruning)하면서 시간복잡도를 줄이는 방법
1-3-1 N-Queen문제
1. N*N 체스판에 N개의 퀸을 배치할 수 있는 경우의 수를 센다.
2. 퀸은 상하좌우, 대각선 방향으로 거리 제한 없이 이동할 수 있다.
3. N=8인 경우, 경우의 수는 다음과 같다.
=> 64 * 63 * ... * 57 = 178,462,987,637,760
=> C 기준 모든 경우의 수를 탐색하는데 약 20.6시간이 소요된다
💡 부모가 안되는 가지는 탐색하지 않음 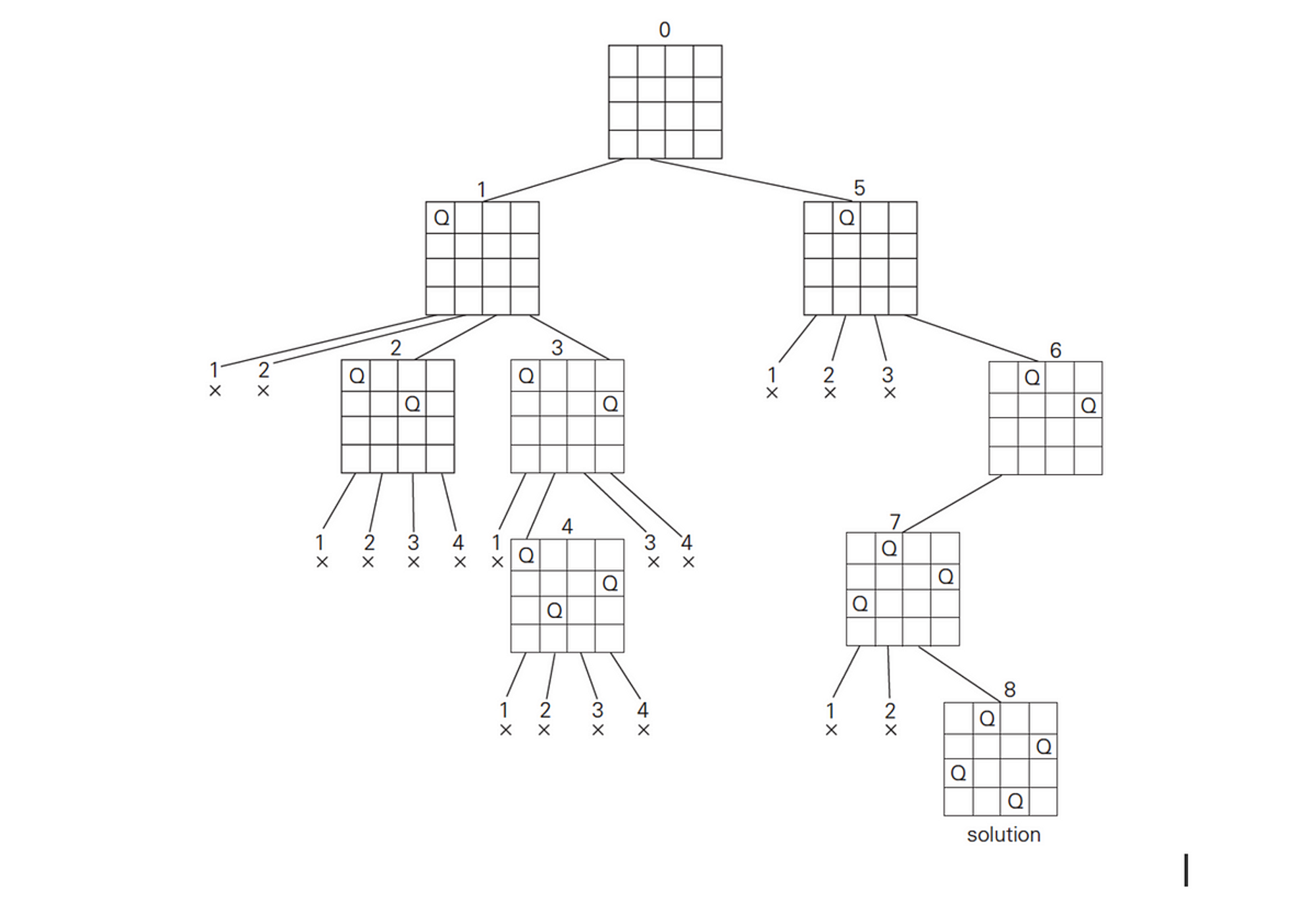
문제풀이
2. 문제풀이
2-1 11866. 요세푸스
from collections import deque 의
deque.rotate() 활용
n > 0 --> rotate(n) = pushleft(pop())
n < 0 --> rotate(n) = push(popleft()) 2-2 1927. 최소 힙, 11279. 최대 힙
파이썬에 내장된 heapq를 사용 (최소 힙)
최대 힙 구현 = 음수로 넣어주면 됨2-3 1037. 약수
(가장 작은 약수) X (가장 큰 약수) = Nint형태의 list로 받기: list(map(int, input().split()))
list안의 nim,max 구하기: max(list), min(list)
2-4 1021. 회전하는 큐
1. 첫 번째 원소가 원하는 원소(=k)여야함!
2. 양쪽 중 가까운 곳은? deq.index(k) <= N/2+1
3. 뽑은 원소는 없어진다.
