이진 트리
1. 자료구조 알고리즘 3주차 강의
1-1 Tree
:계층형 비선형 자료 구조
1-1-1 트리 자료구조
비선형 자료구조: 관계(표현) 중심의 자료구조
💡 선형 자료구조 : 스택, 큐 등
계층형: 비선형 자료구조 중 트리는 계층이 뚜렸하게 나뉜다
1-1-2 용어
Node: 트리에서 데이터를 저장하는 기본 요소
Root Node: 트리 맨 위에 있는 노드
Level: 최상위 노드를 Level 0으로 하였을 때,
하위 Branch로 연결된 노드의 깊이를 나타냄
Parent Node: 어떤 노드의 상위 레벨에 연결된 노드
Child Node: 어떤 노드의 하위 레벨에 연결된 노드
Leaf Node(Terminal Node): Child Node가 하나도 없는 노드
Sibling: 동일한 Parent Node를 가진 노드
Depth: 트리에서 Node가 가질 수 있는 최대 Level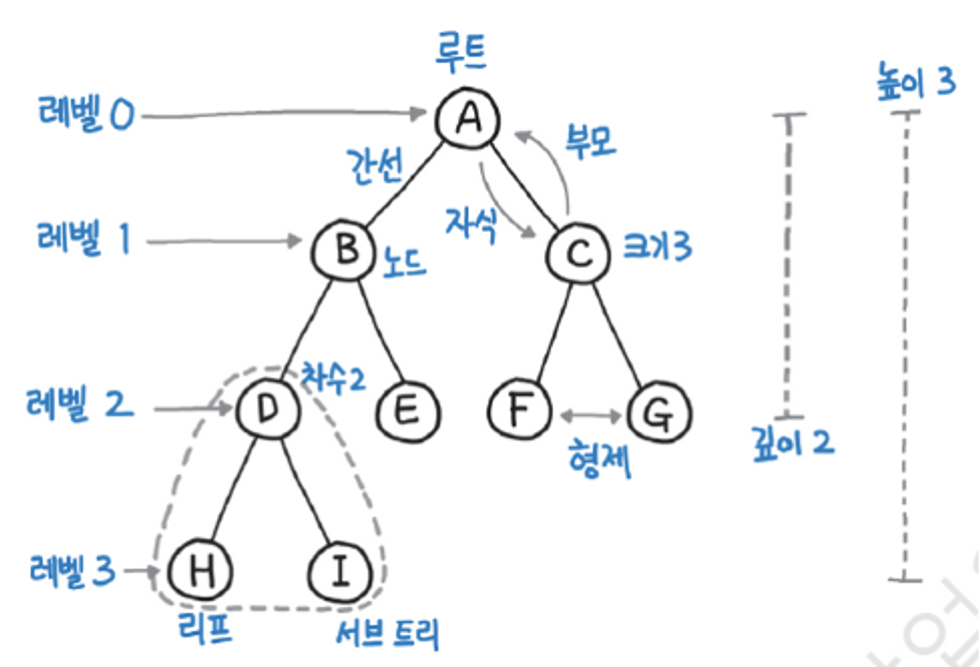
1-1-3 종류
이진 트리 -> 이번 강의에서 다룸
완전 이진 트리 -> 이번 강의에서 다룸
이진 탐색 트리
균형 트리(AVL 트리, red-black 트리)
이진 힙(최대힙, 최소힙)...
1-2 이진 트리
:각 노드가 최대 두 개의 자식을 가진다
1-3 완전 이진 트리
:최하단 왼쪽 노드부터 차례대로 값을 삽입
1-3-1 특징
1. 배열로 표현 가능 -> 넣는 순서가 정해져 있기 때문
2. 레벨=k => 레벨안에 삽입 가능한 노드의 개수는 2^k 개
3. 높이=h => 삽입 가능한 노드의 개수 = 2^(h+1)-1
4. 노드의 개수 = x
2^(h) < x+1 <= 2^(h+1)
h < log2(x+1) <= h+1
==> O(log(x))
5. 자식 노드의 번호(index)
부모의 index = i
left = (i*2)+1
right = (i*2)+2
1-4 이진 탐색 트리
:부모 기준 왼쪽에는 작은 값, 오른쪽에는 큰 값을 가지는 이진 트리
1-4-1 특징
1. 평균적으로 탐색의 시간복잡도는 O(logN)치우친(skewed) 경우 O(n)
2. 치우친(최악의) 경우 O(n) => 균형이 중요! 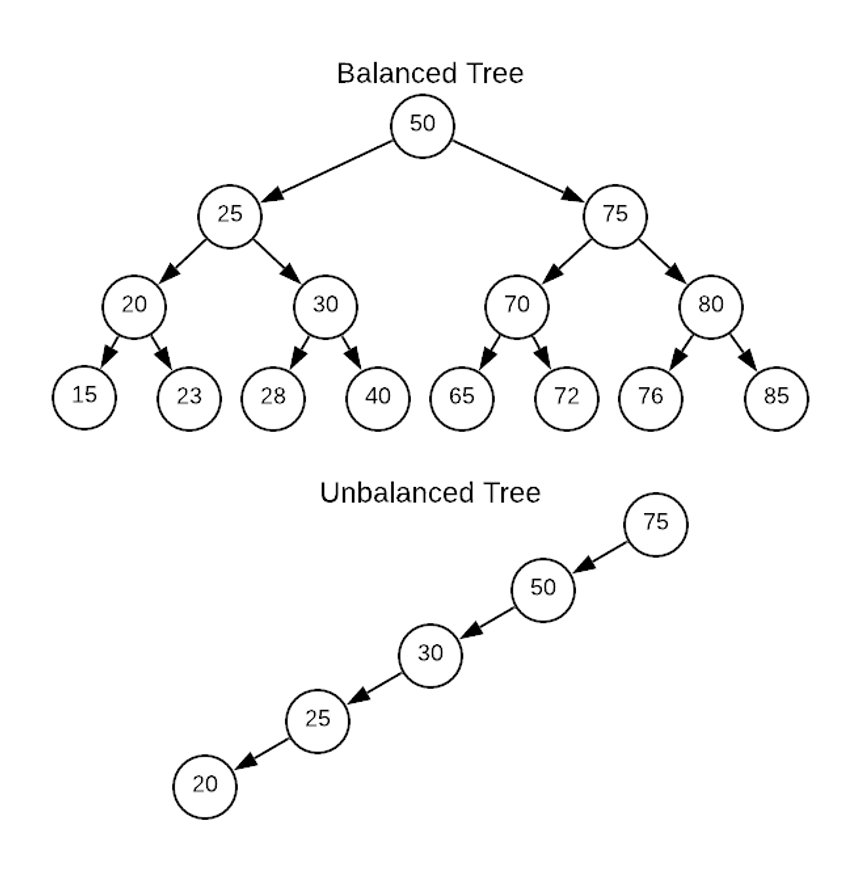
문제풀이
2. 문제풀이
2-1 11047. 동전 0
그리즈만 알고리즘을 이용
1. 가장 큰 동전(c)부터 K와 비교
2. while c <= K: k-c
3. k == 0 이면 종료2-2 11050. 이항 계수 1
def factorial(n): 함수 정의
nCk = N! / ( K! X (N -K)!) 2-3 1547. 잃어버린 괄호
그리즈만 알고리즘을 이용
1. '-' 기준으로 나눈다
=> - 뒤에 값들은 모두 더해 빼야 최소값
2. 첫 번째 index는 sum변수에 더해야 함
3. 나머지는 모두 빼면 됨백준문제풀이
3. 백준문제풀이
1000, 1001,
1003. 피보나치 함수
전역변수로 풀기가 가능하나 시간초과!
n = 입력 값
Z(n) = 총 0의 개수
O(n) = 총 1의 개수
Z(n) = Z(n-1) + Z(n+2)
O(n) = O(n-1) + O(n+2) 가 성립.
따라서 Z(0), Z(1), Z(2) 를 구하면 나머지 값도 알 수 있다.
따라서 O(0), O(1), O(2) 를 구하면 나머지 값도 알 수 있다.-
수 찾기
1.이진 탐색을 이용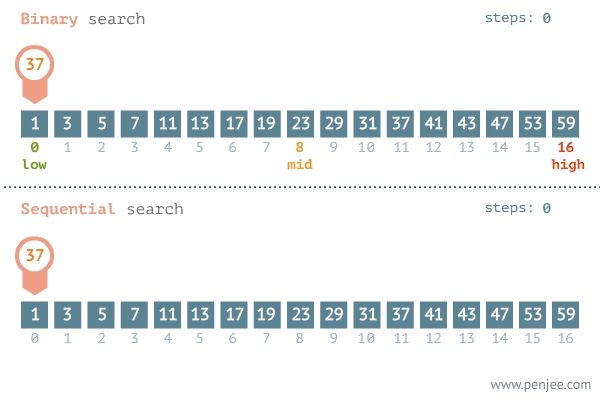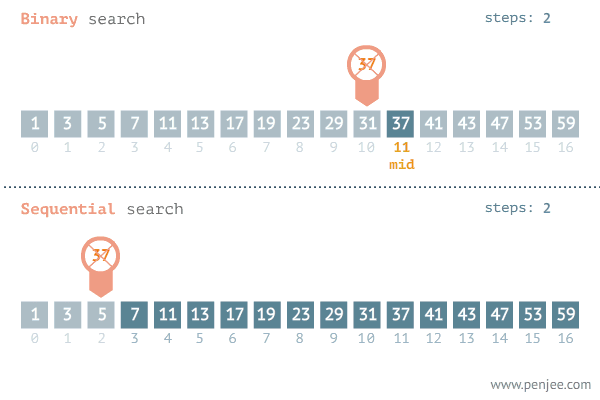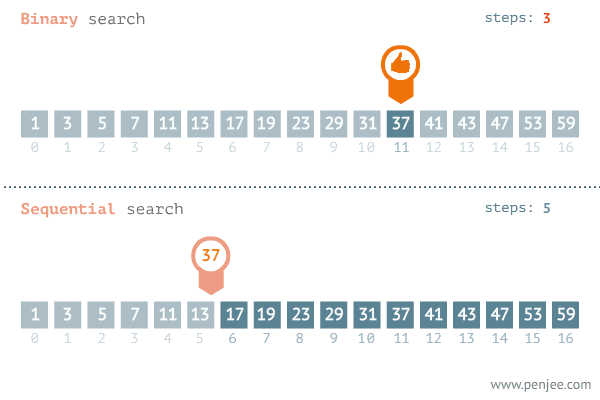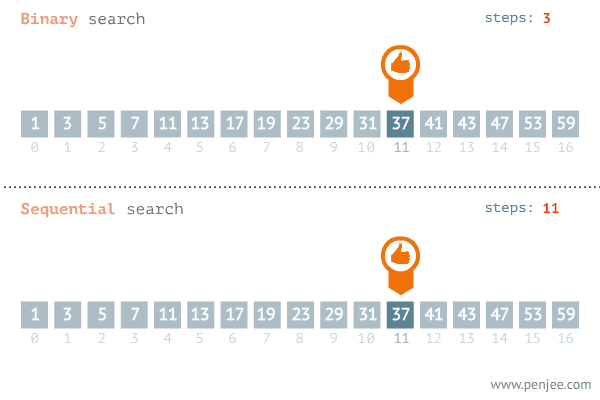
2. set을 이용 set의 특징 : 중복을 허용하지 않는다. 순서가 없다(Unordered).끝
