[Attention Is All You Need]-Transformer 논문 리뷰

1. Introduction

• 그간 sequence modeling이나 language modeling은 recurrent neural network에 의해 진행되어 왔다. (sequence modeling이나 language modeling은 시그널 데이터, 언어 데이터와 같은 시계열 데이터를 사용해 특정 task를 해결하기 위한 혹은 그러한 데이터 생성을 위한 모델 설계와 학습을 의미한다고 이해하였습니다.)

• 그러나 이러한 RNN은 메모리의 제한으로 인해 sequential nature를 완변히 반영하기에 제한된다.

• 이러한 문제점을 해결하기 위해 sequential data의 길이 혹은 데이터 사이의 거리에 의존하지 않는 'Attention mechanism'이 제안되기는 하였지만 여전히 RNN과 함께 사용되기 때문에 언급된 문제를 본질적으로 해결할 수 없다.

• 따라서 우리는 attention mechnism만을 이용한 'Transformer architectur'를 제안한다.

2. Background

본 섹션에서는 계속해서 'attention'과 'self-attention' mechanism에 대해 언급한다. 그러나 기존에는 이러한 메커니즘들이 RNN과 연결되어 사용되어 왔고 Transformer는 RNN 없이 attention으로만 구성된 최초의 모델임을 언급한다.

기존의 이러한 메커니즘들에 대해서는 딥 러닝을 이용한 자연어 처리 입문 사이트를 활용하시기를 적극 추천드립니다. 상당히 자세히 설명되어 있고 코드와 간단한 실험들도 있어서 참고하기 좋습니다.

3. Model Architecture

3.0 Data notation

본 논문에서 사용되는 몇가지 표기와 모델 구조는 다음과 같습니다. 또한 용이한 이해를 위해 몇가지 파트의 설명 순서를 조정하였습니다.

• Transformer는 일반적은 neural transduction model들과 같이 encoder와 decoder로 구성.
• Encoder는 Input $\mathbf{x}=(x_{1},\cdots,x_{n})$를 $\mathbf{z}=(z_{1},\cdots,z_{n})$로 변환.
• Decoder는 $ $\mathbf{z}$가 주어졌을 때 output $\mathbf{y}=(y_{1},\cdots,y_{m})$을 생성하며 이러한 과정은 auto-regressive하게 진행된다. ($y_{m}$을 생성하기 위해서 $(y_{1},\cdots,y_{m-1})$을 decoder의 input으로 다시 투입시킨다는 이야기 입니다.)

3.2 Attention

3.2.1 Scaled Dot-Product Attention

본 섹션은 'self-attention'을 기준으로 설명드리겠습니다. Attention 이해에 있어 가장 중요한 것중 하나는 query, key, value의 개념입니다.

• query: 아웃풋을 산출해내기 위한 기준이 되는 인풋입니다. 예를들어 $x_{1}$의 output $z_{1}$을 얻어내기 위해서는 query를 $1$로 설정합니다.
• key: key에 대해서 attention score를 얻기 위한 후보들입니다.
• value: 최종 임베딩을 얻기 위한 임베딩 벡터입니다.

수식을 통해서 보여드리겠습니다. 예를들어 data notaion의 상황에서 $x_{1}$이 query로 설정되었다면 다음과 같은 수식에 따라 ouput $z_{1}$이 산출될 수 있습니다.

• $x_{n} \in \mathbb{R}^{1\times d}$
• query embedding $x^{q}_{1} = x_{1}W^{Q}\; where\;W^{Q}\in\mathbb{R}^{1\times d_k}$
• key embedding $x^{k}_{i} = x_{i}W^{K}\; where\;W^{K}\in\mathbb{R}^{1\times d_k}$
• value embedding $x^{v}_{i} = x_{i}W^{V}\; where\;W^{K}\in\mathbb{R}^{1\times d_v}$
• 각 key들에 대한 $attention\;score = softmax(x_{1}^{q}(x_{1}^{k})^{T},\cdots,x_{n}^{q}(x_{1}^{k})^{T})$이고 각 key에 대한 attention score는 $s^{q}_{i}$라 하겠습니다
• 최종 $z_{1} = \sum_{i}s_{i}^{q}x_i^{v}$

수식을 통해보니 알고리즘이 좀 더 잘 이해가실까요? 결국 attention이란 query를 기준으로 key들과의 attention score를 구해내고 해당 score의 중요도에 따라(곱해주는 것으로) value들의 weighted sum을 진행하는 것과 같습니다. 이러한 attention을 제가 보여드릴 예시처럼 input 내부에서만 진행한다면 self attention, query를 input이 아닌 외부에서 갖고온다면 attention이 됩니다. 또한 위 식들의 4번 과정에서 dot-prouct에 softmax를 취해 attention score를 구하는 것은 dot-product attention이고 key, query embedding들을 mlp에 투입해 attention score를 계산하는 것은 addictive attention이라 한다네요. 본 논문에서는 dot-product attention을 사용한다고 합니다.

물론 제가 예시로 보여드린 것처럼 하나의 key에 대해서만 계산하지는 않고 모든 input들에 대해 matrix 형태로 계산하는데 식은 아래와 같습니다.

• $Attention(Q, K, V)=softmax({{QK^{T}}\over{\sqrt{d_{k}}}})V\;where\;Q,V\in\mathbb{R}^{n\times d_{k}}, V\in\mathbb{R}^{n\times d_{v}}.$

근데 저는 지금까지 $\sqrt{d_K}$로 softmax 내부의 값을 나눠주는 이유가 gumble softmax의 relaxation과 같이 attention score의 값을 일정하게 배분하기 위함이라고 생각하고 있었습니다만 본문에는 $d_{k}$ 값이 커서 dot product의 값이 커지기 때문에 gradient가 작아지는 것을 방지함이라고 하네요 ... 이부분에 대해서 softmax의 backpropagation을 복습해 보았는데 지금의 저로서는 100% 이해하기는 어려울 것 같습니다. 죄송합니다만 혹시 다시 학습할 기회가 생긴다면 조금 더 깊게 공부해보도록 하겠습니다! 참고로 논문에서 제시한 figure는 아래와 같이 매우 심플하게 그려져 있습니다.

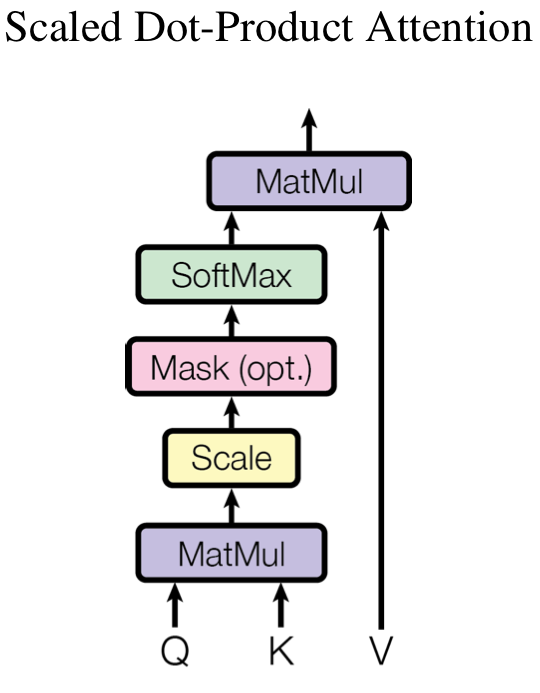
위그림을 보시면 Mask block이 있는데 이는 추후 decoder 파트에서 다루겠지만 특정 key-value의 score를 보지 않기위해 masking을 씌우는 block입니다. 간단하게 설명드리자면 attention score를 구하기 위해 $QK^{T}$가 softmax를 지날 때 해당부분의 output을 $-\infin$으로 처리해주면 됩니다. 이렇게 할경우 softmax 내부에서 exponential을 취할 때 해당 부분의 score가 0이 되므로 value embedding과 곱해질 때 해당 score를 고려하지 않을 수 있게 됩니다.

3.2.2 Multi-Head Attention

Multi-head attention은 attention을 여러번 (여러개의 head)로 진행하는 것입니다. 본문에는 자세히 나와있지 않지만 제가 처음에 transformer를 공부할 때 'multi-head를 사용하는 것이 전혀 다른 여러개의 perspective를 학습하기 위해서가 아닐까?' 생각했던게 기억이 납니다.

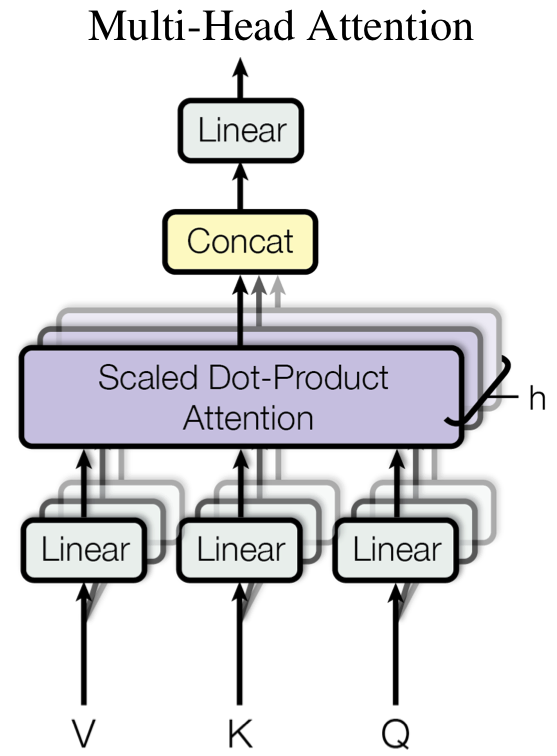
논문 내의 figure는 위와 같은데 여러 개의 head로 attention을 진행하는 것을 알 수 있습니다. 수식은 아래와 같이 아주 간단합니다.

• $MultiHead(Q, K, V) = Concat(head_{i},\cdots,head_{h})W^{O}\; where \; head_{i}=Attention(W_{i}^{Q}Q,W_{i}^{K}K, W_{i}^{V}V )$
• $W_{i}^{Q}, W_{i}^{K}\in\mathbb{R}^{d_{model}\times d_{k}}, W_{i}^{V}\in\mathbb{R}^{d_{model}\times d_{v}}, W_{O}\in\mathbb{R}^{hd_{v}\times d_{model}}$

이때 head의 갯후 $h=8$로 설정하고 $d_{k},d_{v}=d_{model}/h=64$로 설정하였다고 합니다. 또한 이러한 설정은 head가 늘어남에 따라 $d_{k}, d_{v}$에 연산에 필요한 비용을 줄임으로써 multi-head attention도 single-head attention과 동일한 비용을 사용하기 위함이라고 합니다.

3.1.1 Encoder and Decoder Stacks

Transformer의 최종 architecture는 아래 그림과 같습니. Encoder는 residual connection과 layer-normalization을 사용했다는 것 외에는 특별한 특징은 없습니다. 본 문에서는 output dimension $d_{model}= 512$, 총 레이어의 갯수 $N=6$으로 설정했다고 합니다.

Decoder또한 $N=6$층으로 구성되어 있습니다. 또한 masking 기법을 활용하여 i번째 임베딩에는 i이전의 토큰들만 사용됩니다. 또한 그림을 보시면 decoder의 두번째 multi-head attention layer는 encoder로 부터 정보를 받는데 이는 3.2.3절 에서 알아보도록 하겠습니다.

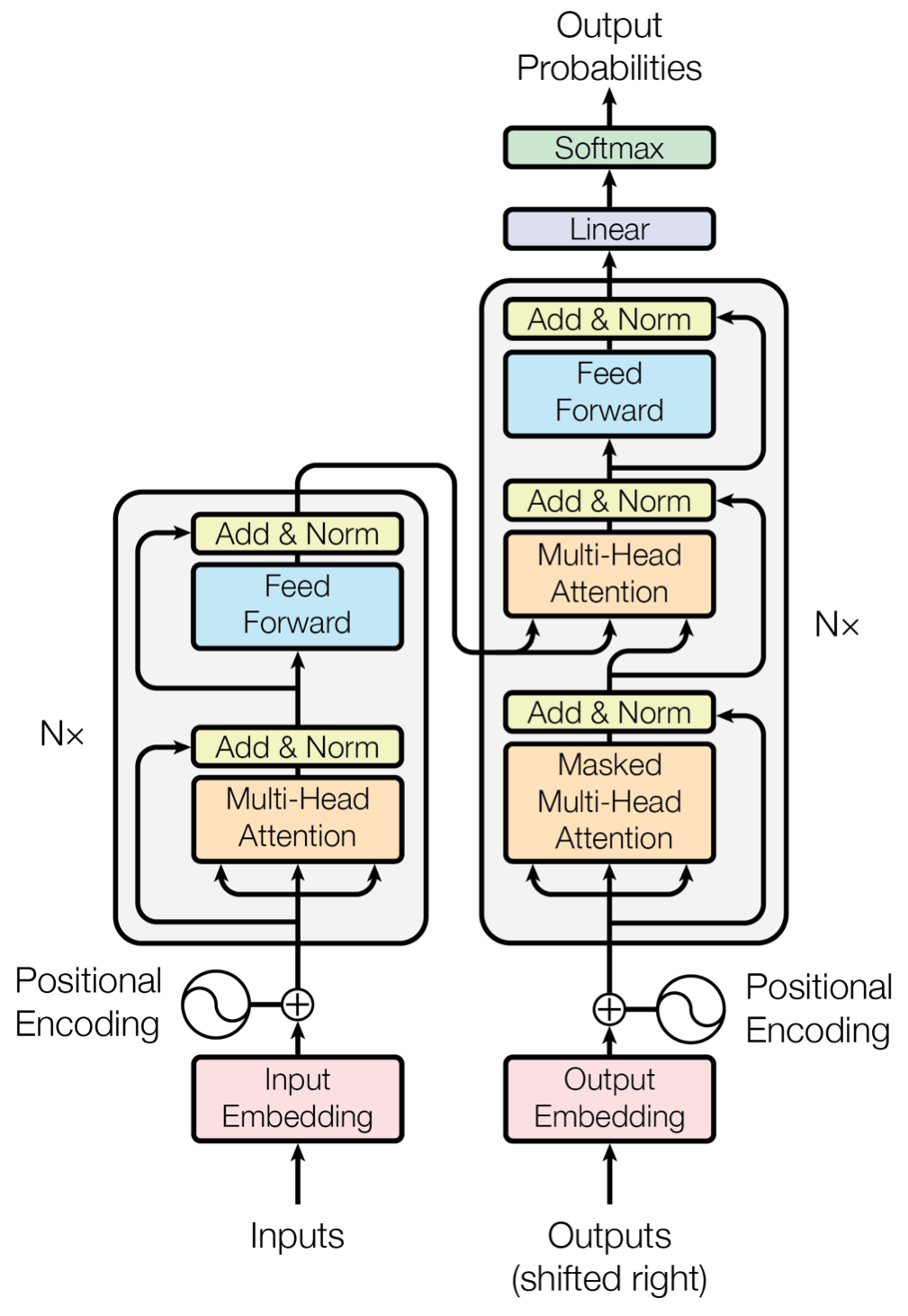
3.2.3 Applications of Attention in our Model

트랜스포머의 멀티헤드 어탠션은 다음과 같은 세가지를 고려하여 설계 되었습니다.

• 그림에서 볼 수 있듯이 decoder의 순전파 시 encoder의 키, 밸류를 가져와 어탠션을 진행합니다. 이러한 특성을 Encoder-decoder attention라고 합니다.
• Encoder의 attention은 전 층의 attention 결과를 인풋으로 하여 생성됩니다.
• Decoder의 attention은 생성 모델에서 auto-reggresive한 성질을 반영하여 진행됩니다. (auto-reggresive한 성질이란 시계열 데이터의 i-time의 데이터 생성시 i 이전까지의 정보를 사용한다는 의미입니다. 즉, 마스킹을 활용한다는 뜻.)
  

3.3 Position-wise Feed-Forward Networks

그림에서 position-wise Feed-Forward Networks에 해당하는 부분입니다. 트랜스포머에서는 어탠션 후의 feed-feed network를 진행할 때 각각의 토큰 별로 다음과 같은 식에 의해 따로 진행한다고 합니다.

• $FFN(x)=max(0,xW_{1}+b_{1})W_{2}+b_{2}$
  

3.4 Embeddings and Softmax

해당 파트의 맨 첫번째 문장 'Similarly to other ...'을 솔직히 잘 이해가 안되네요... input token을 output token으로 바꾸기 위해 linear layer를 사용한다고 했는데 이게 트랜스 포머 내의 Feed-Forward network와 유사한 역할을 하는 또 다른 네트워그아 있다는 건지... 일단 뒷 내용은 decoder에서 next token을 맞추기 위한 linear layer와 softmax layer를 사용한다고 하는 것 같습니다.

3.5 Positinoal Encoding

위 까지 설명드린 트랜스포머의 구조는 positional한 정보를 반영하지 못합니다. 따라서 아래와 같은 token input embedding에 positional encoding을 더 해줘야합니다. Positional encoding은 다음과 같은 식에 따라 정해집니다.

• $PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})$
• $PE_{(cos,2i+1)}=sin(pos/10000^{2i/d_{model}})$
  

4. Why Self-Attention

저자들은 self-attention을 사용하는 이유를 다음과 같이 2가지로 설정하였습니다.

• Layer당 total computation의 양
• 필요한 parallelize 될 수 있는 sequential operation의 양
• 서로 관여할 수 있는 data의 길이 (long-range dependence라고 표현합니다.)
  

위 표를 보시면 트랜스 포머느 고정된 길이에서는 한번의 operation (sequential operation)으로 모든 길이의 포워딩을 진행할 수 있습니다. 하지만 RNN은 데이터의 길이 (n)만큼 operation이 필요합니다.

5. Training

트레이닝 디테일은 특별 사항이 없어 패스합니다 :)

6. Results

실험 또한 패스하겠습니다 ..!