[통계 이론] z-검정(z-test)

robin·2021년 8월 28일

z-검정 z-분포 z-점수 표준화

통계 이론

목록 보기

5/5

표준화

필요성: 측정하는 단위가 달라서 원점수별 비교가 어려운 문제가 있음.

예) A 테스트는 점수가 0점~100점, B 테스트는 점수가 0점~80점 일 때 A 테스트에서 80점과 B 테스트에서 80점을 어떻게 비교할 것인가.
원점수(raw score)를 표준점수(standard score)로 변환함.

z-score (z-점수 또는 표준점수)

어떤 원점수도 z-점수로 변환할 수 있음.
z-점수는 평균으로부터 몇 SD 큰지, 작은지 나타냄.
예: z-점수가 1이면 평균보다 1SD 크다.
z-점수가 + 이면 원점수가 평균보다 크다는 것을 의미하고, -이면 원점수가 평균보다 작다는 것을 의미함.
어떤 분포를 가진 점수도 z-점수로 변환할 수 있으며, z-점수로 변환한다고 해서 원점수의 분포가 바뀌지 않음.
정규분포만 z-점수로 변환할 수 있는 것은 아님. 다만, 정규분포에서 z-점수가 유용하게 사용될 수 있음.

z-점수 기본 공식

$z = \frac{x – μ}{σ}$

표집분포의 원점수를 z-점수로 표준화하기

$z = \frac{\overline{X} – μ}{\frac{σ}{\sqrt{N}}}$

중심극한정리로 인해 $μ_{\overline{x}} = μ$ , $σ_{\overline{x}} = \frac{σ}{\sqrt N}$

z-distribution (z-분포)

평균은 0, 표준편차는 1인 정규 분포
특정한 값이 평균으로부터 몇 SD 떨어져 있는지 안다면(즉, z-점수를 안다면) 그 값보다 크거나 작은 값을 얻을 확률을 구할 수 있음.

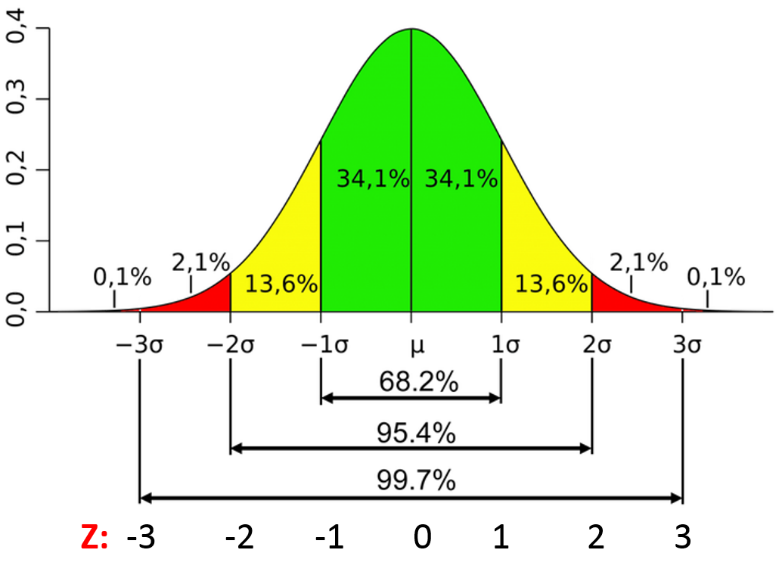
<예시>

평균보다 1SD 작은 값보다 작은 값을 얻을 확률은 얼마인가? ➡️ z-점수가 -1인 경우에 그보다 작은 값을 얻을 확률이므로 P = 13.6 + 2.1 + 0.1 = 15.8%
평균보다 1SD 큰 값보다 작은 값을 얻을 확률은 얼마인가? ➡️ z-점수가 1인 경우에 그보다 작은 값을 얻을 확률이므로 P = 34.1 + 34.1 + 13.6 + 2.1 + 0.1 = 84%

z-test(z-검정)

z-분포를 이용하여 가설을 검정하는 통계적 방법.
모집단의 평균과 표준편차를 알 수 있어야 함.
표본의 크기가 크거나 (n > 30) 모집단의 정규분포여야 함.
등분산 가정이 충족될 때 사용함. 두 모집단을 비교할 경우 두 모집단의 분산이 같아야 함.

(1) 단일 표본 z-검정 (one sample z-tset)

모집단을 대표하도록 추출된 표본의 평균을 연구자가 이론적 혹은 경험적으로 얻은 특정한 값과 비교하는 통계적 방법.

<예제>
[문제]
백문이불여일타아카데미에서 수년간 파이썬 강의를 통한 파이썬 코딩 평균 점수가 80점이었고 표준편차는 15점이었다. 이번학기에 프로젝트를 활용한 파이썬 수업을 100명의 수강생들에게 실시하였고, 파이썬 코딩 평균 점수는 85점이었다. 새로운 강의 방식에 따른 수강생들의 평균 점수 85점이 80점과 같은지 유의수준 .05에서 검증하라.

[풀이]

귀무가설: 새로운 강의 방식에 의한 파이썬 코딩 평균 점수는 80점과 같다.
$\mu = 80$
대립가설: 새로운 강의 방식에 의한 파이썬 코딩 평균 점수는 80점이 아니다.
$\mu ≠ 80$

z = $\frac{{85} – 80}{\frac{15}{\sqrt{100}}}$ = 3.33

유의수준 .05에서 기각값은 $\pm$ 1.96이다.

새로운 강의 방식에 의한 파이썬 코딩 평균 점수 85점의 z-점수는 3.33이어서 1.96보다 크기 때문에 귀무가설을 기각한다.

따라서 유의수준 .05에서 새로운 강의 방식에 의한 파이썬 코딩 평균 점수는 80점이 아니다.

(2) 독립 표본 z-검정 (independent sample z-tset)

두 모집단의 평균을 비교하기 위해서 각 모집단을 대표하도록 추출된 독립적인 두 표본을 비교하여 두 모집단을 비교하는 통계적 방법.
두 모집단의 분산이 동일하다는 것을 이론적 혹은 경험적 배경을 통해 알고 있어야 함.

z-score 공식

$z = \frac{(\overline{X_{1}} - \overline{X_{2}}) - (\mu_{1} - \mu_{2})}{\sqrt{ \frac{\sigma_{1}^{2}}{n_{1}} + \frac{\sigma_{2}^{2}}{n_{2}}}}$

<예제>
[문제]
전국 30세 남녀 각각 100명을 무작위 추출하여 체중을 측정했다. 남성의 체중 평균은 68kg, 여성의 체중 평균은 60kg였다. 연구자는 이론적 배경에 의해 30세 남성 모집단의 체중 표준편차는 10kg이고 여성 모집단의 체중 표준편차는 9kg임을 알고 있다. 30세 성인 남녀의 체중에 차이가 있는지 여부를 유의수준 .05 수준에서 검정하라.

[풀이]