[A/B Test] Thompson Sampling

안녕하세요! 오늘은 A/B Test에 자주 쓰이는 방법인 Thompson Sampling에 대해 알아보겠습니다. 이 방법은 베이지안 추론을 바탕으로 설계되었는데요, 통계학을 전공하면서 베이지안 추론에 대해 배운적이 있는데 그 내용이 그대로 녹아있더라고요! 아마도 베이지안 통계학을 배워보신분이라면 아주 쉽게 이해하실 수 있을거에요.

A/B Test에서 Thompson Sampling의 목표는 기회비용을 줄이는 것인데요! 쉽게 말하면, A/B Test에서 KPI달성에 낮은 성능을 보이는 전략을 점점 낮게 적용하며, 반대로 높은 성능을 보이는 전략을 더욱 많이 적용하는 방식으로 A/B Test를 진행하며 이에 따르는 손실을 최소화하는 것입니다!

A/B Test에서 이러한 목표를 이루기위한 다른 방법들이 많이 존재하지만, 요즘에는 Thompson Sampling이 가장 많이 쓰이는 방법이라고 합니다.

내용은 A tutorial on Thompson Sampling을 바탕으로 작성하였습니다.

Multi Armed Bandit Problem

Multi Armed Bandit 이란 단어는 카지노에서 처음으로 쓰인 단어라고 합니다.

• 한 도박꾼이 카지노의 슬롯 머신을 돌려 최대한 많은 돈을 벌고자 합니다. 여기서 각각의 머신은 다른 분포를 따르며 돈을 내놓게 됩니다. 이 도박꾼이 카지노에서 최대한의 이득을 보기위해 여러 슬롯머신을 실험하며 슬롯 머신의 패턴을 파악하고자 합니다. 이때 파악한 패턴을 통해 가장 많은 수익을 낸 머신에 남은 돈을 모두 써버리기에는 정보가 너무 부족하고, 더 많은 정보를 얻기 위해 더 많은 실험을 하는 것은 큰 지출을 발생시킵니다.

이러한 문제를 Multi Armed Bandit Problem이라고 하며 Thompson Sampling은 이 문제의 전략 중 하나입니다.

Multi Armed Bandit Problem은 현실에서 종종 볼 수 있는데, 대표적으로 기업들의 광고전략 비교 등의 문제로 많이 다루어지며, 우리에게 친숙한 추천시스템, UI 비교 등 사전에 어떠한 지표의 측정이 어려운 문제들에 대하여 A/B Test를 진행할 때 다루게 됩니다.

Thompson Sampling

앞서 말씀드렸듯이 Thompson Sampling은 최근의 Multi Armed Bandit Problem에서 좋은 성능을 내고 있으며, 요즘 널리 사용되는 방법입니다. Thompson Sampling의 방법을 대략적으로 설명하면

1. K개의 전략의 사전분포에서 표본을 추출하며 가장 큰 값을 갖는 표본의 전략을 선택합니다.

2. 선택된 적략을 통해 실험하며, 실험결과를 통해 사후분포를 얻습니다.

3. 사후분포(Posterior distribution)를 새로운 사전분포로 적용하여 다시 1.을 실행합니다.

이 과정을 일정 시간, 횟수만큼 반복하게 됩니다.

기본적인 골자는 이렇게 진행되지만, 이 포스트에서는 가장 많이 이용되며 가장 간단한 Bernoulli 케이스를 들어 더욱 자세하게 설명하겠습니다.

우리가 어떠한 $K$개의 후보 광고페이지 중 어떠한 광고페이지가 가장 많은 클릭을 발생시킬 수 있는지 알고 싶다고 가정하고 계속해서 설명하겠습니다.

Posterior Distribution

우선 Bernoulli 케이스에서의 Thompson Sampling을 알아보기전에 Baysian방법을 통해 사후분포를 구하는 방법부터 알아보겠습니다.

$k$번째 광고페이지는 $\theta_k$의 확률로 클릭을 발생시킨다고 합시다. 즉, $X_k$를 $k$번째 페이지에 대한 클릭이라고 할때, $X_k \sim Bern(\theta_k)$입니다.

우선 $\theta_k$의 사전분포를 $Beta(\alpha_k, \beta_k)$라고 가정해봅시다.

• 대게 사전 정보가 없기 때문에 $\alpha_k$ = 1, $\beta_k$ = 1로 두고 시작합니다. 이 경우는 Uniform 분포와 동일합니다.

• 베타분포는 여러 부분에서 많이 쓰이지만 다음과 같은 이유로 Bernoulli 분포의 모수에 대한 사전분포로 많이 이용됩니다.

  • 계산이 매우 편리합니다.

  • 예를 들어 10번의 방문 중 5번의 클릭이 있었을 경우, $\theta_k$ 값은 0.5로 추정할 수 있지만 그 신뢰도가 약합니다(분산이 큼). 하지만 200번의 방문 중 100번의 클릭이 있었을 경우 마찬가지로 $\theta_k$ 값을 0.5로 추정할 수 있지만 그 신뢰도가 큽니다(분산이 작음).

    • $Beta(5,5)$ 의 평균은 $0.5$이며, 분산은 $0.0228$.

    • $Beta(100,100)$ 의 평균은 $0.5$이며, 분산은 $0.0012$.

  

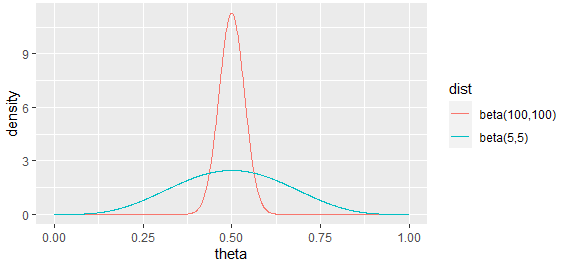
이때 $k$번째 광고페이지에서 클릭이 발생한 경우 $\theta_k$의 사후분포는 $Beta(\alpha_k+1, \beta_k)$ 발생하지 않은 경우 $Beta(\alpha_k, \beta_k+1)$ 을 갖게 됩니다. 이 계산은 다음을 참고하시면 됩니다.

이것을 확률분포를 이용해 설명하면 $\theta_k$의 확률 밀도함수 $p(\theta_k) = \frac{\Gamma(\alpha_k + \beta_k)}{\Gamma(\beta_k)\Gamma(\alpha_k)}\theta_k^{(\alpha_k-1)} (1-\theta_k)^{(\beta_k-1)}$ 이기 때문에

$\hspace{12mm}p(\theta_k \mid X_k = x_k) \propto p(\theta_k)\cdot p(X_k = x_k \mid \theta_k) \propto \theta_k^{(\alpha_k-1)+ x_k}(1-\theta_k)^{(\beta_k-1) +1-x_k}$

인데요.

이것을 이용하면 (확률밀도함수에서 $\theta_k$의 함수적 관계를 보면 베타 분포임을 알 수 있습니다.)

$\hspace{30mm}\theta_k \mid X_k = x_k \sim Beta(\alpha_k +x_k, \beta_k+1-x_k)$

임을 알 수 있습니다.

즉, $\theta_k$의 사후분포는 클릭이 발생한 경우 $Beta(\alpha_k +1, \beta_k)$, 그렇지 않은 경우 $Beta(\alpha_k, \beta_k+1)$이 됩니다.

• 여기서 사전분포와 사후분포가 모수만 다른 같은 분포를 가지게 되는데요 이것을 공액사전분포(Conjugate prior distribution)라고 합니다.

다시 Thompson Sampling으로 돌아와서 Bernoulli case에서의 방법은 아래와 같습니다.

1. K개의 사전분포에서 $\hat{\theta}_k$를 샘플링하여 가장 큰 값을 갖는 $\hat{\theta}_k$의 인덱스$(x_t \in \{1,...,K\})$를 얻습니다.

2. $x_t$에 해당하는 광고페이지를 통해 실험하며, 실험결과를 통해 사후분포를 얻습니다.

3. 사후분포를 새로운 사전분포로 적용하여 다시 1.을 실행합니다.

이 원리에 대해 조금 더 자세히 설명하면, $Beta(\alpha, \beta)$의 평균과 분산은 각각 $\frac{\alpha}{\alpha+ \beta}$, $\frac{\alpha\beta}{(\alpha+ \beta)^2(\alpha+\beta+1)}$입니다. 즉 Thompson Sampling의 iteration이 진행됨에 따라 평균에 가까운 표본이 많이 추출되고 이러한 경향으로 인해 더 높은 클릭확률을 갖는 광고페이지를 더 많이 노출하게 됩니다.

결과적으로 노출되는 확률을 살펴보시면 (action1, 2, 3의 참 $\theta$값은 각각 0.9, 0.8, 0.7)

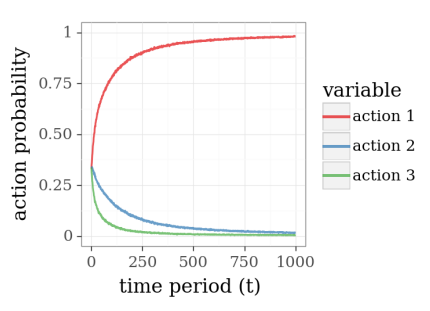
으로 참 $\theta$ 값이 가장 큰 action 1을 점차 많이 노출하게 됩니다.

Conclusion

A/B Test를 통해 실험을 할때에 동일한 비율로 광고를 노출하게 되면 클릭률이 낮은 광고페이지를 자주 노출하게 되어 기회비용이 발생하지만, Thompson Sampling을 통해 이 기회비용을 크게 줄일 수 있습니다.

또한 광고페이지처럼 클릭함/ 클릭하지 않음과 같은 이진변수가 아니더라도 Count일 경우 Poisson, 연속형일 경우 Gaussian분포를 적용하여 Thompson Sampling으로 A/B Test를 진행할 수 있을 것으로 보입니다. (두 분포 모두 공액사전분포가 존재하기 때문입니다.) 다만, Bernoulli분포보다 더 강한 가정으로 보입니다..