[Causal Inference] Introduction To Causality

안녕하세요. 요즘 인과관계추론에 관심이 많아져 공부를 하는 중에 있는데요!

괜찮은 자료를 발견해서 이 내용을 공부해보고 스텝에 맞게 정리해보고자 합니다. 자료의 출처는 Causal Inference for the Brave and True (https://matheusfacure.github.io/python-causality-handbook/) 입니다.

작성자분께서 굉장히 유쾌하셔서 어려운 내용임에도 불구하고 굉장히 흥미롭게 공부하고 있습니다. 또한 작성자분께서 흔쾌히 공유는 언제든 가능하다고 해주셔서 내용을 포스트하게 되었습니다.

작성내용은 해당 내용의 이해를 바탕으로 정리하기 때문에 틀린 부분이 있을 수도 있습니다! 여러분들도 공부해 보시고 틀린부분이 있다면 지적해주시면 감사하겠습니다!!

Introduction

머신 러닝이 현재 좋은 성능을 보이고 있는 분야는 예측입니다. Ajay Agrawal, Joshua Gans, Avi Goldfarb는 Prediction Machines라는 책에서 "인공 지능의 새로운 파도는 실제로 우리에게 지능을 가져다주는 것이 아니라 지능의 중요한 구성 요소인 예측을 가져다 준다."라고 말했습니다. 우리는 머신 러닝으로 많은 것을 해낼 수 있으며, 유일한 요구되는 것은 문제를 예측 문제로 프레임화하는 것입니다.

하지만 머신러닝은 몇가지 문제점이 있습니다.

• 머신러닝은 현재 아주 제한적인 분야에서 쓰이고 있으며, 그렇지 않은 경우 좋은 성능을 보이지 못하고 있습니다.

• 예를들어, 머신러닝이 "만약에"라는 질문에 답해야 한다면 어떻게 될까요? 예를들어, 상품의 가격을 올리면 어떠한 일이 일어날까요? 이러한 질문의 중심에는 인과관계를 알고자함이 있습니다. 머신러닝으로 이런 종류의 문제를 해결하는 것은 대부분의 사람들이 해결하는 것보다 어렵다고 합니다.

데이터 분석을 해보셨던 분들이라면 "연관관계는 인과관계가 아니다"라는 말을 많이 들어보셨을 것입니다. 그러나 실제로 왜 그런지 설명하는 것은 조금 복잡합니다. 사실 이정도가 인과 추론에 대한 소개의 전부입니다. 이 글의 나머지 부분에서는 연관관계를 어떻게 인과관계로로 만들 수 있는지에 대해 주로 다루어 보겠습니다.

언제 연관관계는 인과관계일까요?

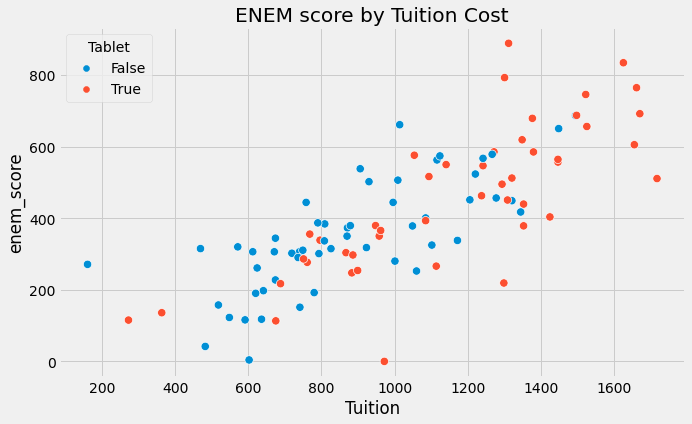
직관적으로 연관성이 인과 관계가 아니라는 것은 잘 알고있습니다. 예를들어, 학생들에게 태블릿을 제공하는 학교가 그렇지 않은 학교보다 더 나은 성적을 받는다고 한다면, 태블릿을 제공하는 학교가 더 부유하기 때문이라는 사실을 눈치채실 수 있을 것입니다. 따라서 태블릿을 제공받지 않더라도 평균보다 더 잘 할수 있는 학생들입니다.

• $T_i$: unit $i$에 대한 treatment여부
  
  
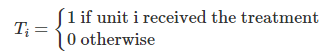
• $Y_i$: unit $i$에 대한 관측된 결과 값
  - $Y_{0i}$: treatment가 없는 경우 unit $i$의 잠재적 결과
  - $Y_{1i}$: treatment가 있는 경우 unit $i$의 잠재적 결과

결과는 관심 변수이며, treatment가 결과 값에 대한 영향의 유무가 주 관심사 입니다. 태블릿 예시에서는 성적이 관심 변수이며, 태블릿의 제공여부가 treatment가 됩니다.

당연하게도 인과 추론에서, treatment를 받거나 받지 않는 경우의 동일한 unit을 관찰할 수 없습니다. 즉, $Y_{0i}$와 $Y_{1i}$는 동시에 관측되지 않습니다.

이 문제를 둘러싸고 우리는 잠재적인 결과 에 대해 많은 이야기를 할 것 입니다. 그들은 실제로 일어나지 않았기 때문에 가능성이 있습니다. 대신 그들은 어떤 치료가 취해진 경우에 일어날 일 을 나타냅니다.

잠재적인 결과로 개별 treatment의 효과를 정의하면 다음과 같습니다.

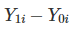
하지만 인과 추론에서 두 값은 동시에 관측될 수 없으므로 다음과 같은 평균 치료 효과(ATE)에 초점을 맞추고 있습니다.

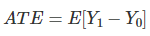
이때 조금 더 추정하기 쉬운 또 다른 값은 treatment에 대한 평균 치료 효과(ATT)입니다.

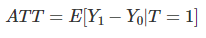
하지만 ATE, ATT모두 잠재적 결과를 알지 못하기에 측정할 수 없습니다..!

만약 우리가 전지전능한 힘이 있어 우의 태블릿 예시에서 treatment에 따른 두 값을 모두 알 수 있다고 가정하고 ATE와 ATT를 계산하여 봅시다. (t: treatment)

$ATE = (-50 + 0 -200 + 50)/4 = -50$

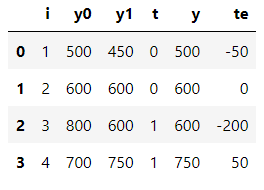
• 이것은 태블릿이 학생들의 성적을 50점 감소시켰음을 의미합니다.

$ATT = (-200 + 50)/2 = -75$

• 태블릿을 제공받은 학생의 경우 태블릿이 학생들의 성적을 평균적으로 75점 감소시켰습니다.

하지만 실제 표를 통해 ATE를 계산해보면,

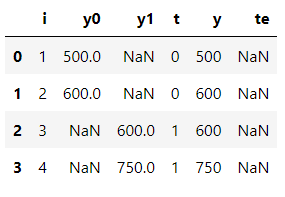
계산할 수 없습니다.. 하지만 $E(Y_1\mid T = 1) - E(Y_0\mid T = 0)$ 을 이용해 계산하여 보면,

$ATE = (600+750)/2 - (500+ 600)/2 = 125$ 로 실제 결과와 아주 크게 다릅니다.. 왜 이런 일이 생겼을까요? 그 답은 연관성을 인과관계로 착각하는 중대한 범죄를 저질렀기 때문입니다! 그 이유에 대해 계속해서 알아보겠습니다.

편향 (Bias)

편향은 연관관계를 인과관계와 다르게 만든다고 합니다! 다음 예시를 보면서 이해해보겠습니다.

• 위의 태블릿 예시를 다시 한번 보겠습니다. 학생에게 태블릿을 제공하는 학교가 더 높은 시험 점수를 얻는다는 주장에, 그러한 학교는 태블릿 없이도 어쨌든 더 높은 시험 점수를 얻을 것이라고 반박할 수 있습니다. 다른 학교보다 돈이 더 많기 때문입니다. 따라서 그러한 학교의 학생은 더 나은 교사에게 더 큰 비용을 지불하고 더 좋은 교실에서 공부할 수 있습니다. 즉, 태블릿 제공여부로 학교들의 학생 성적을 비교할 수 없다는 것입니다.

이제 연관성이 인과관계가 아닌 이유를 수식을 통해서 알아보겠습니다.
연관성은 $E[Y|T=1] - E[Y|T=0]$으로 측정할 수 있습니다. 하지만 인과관계는 $E[Y_1 - Y_0]$으로 측정이됩니다.

연관성을 한번 살펴보겠습니다.

$E[Y|T=1] - E[Y|T=0] = E[Y_1|T=1] - E[Y_0|T=0]$

여기에 $E[Y_0|T=1]$을 빼고 더하여 보겠습니다.

$E[Y|T=1] - E[Y|T=0] = E[Y_1|T=1] - E[Y_0|T=0] + E[Y_0|T=1] - E[Y_0|T=1]$

이때, 이 식은 다음과 같이 ATT와 Bias로 분해가 가능합니다.

$E[Y|T=1] - E[Y|T=0] = \underbrace{E[Y_1 - Y_0|T=1]}_{ATT} + \underbrace{\{ E[Y_0|T=1] - E[Y_0|T=0] \}}_{Bias}$

이 수식을 통해 우리가 알 수 있는것은 연관성을 계산할 때 ATT이외에 Bias의 효과도 함께 계산된다는 것입니다. Bias는 treatment 그룹과 대조군이 treatment 전에 서로 다름에 의해 발생합니다. 즉, 두 실험군 모두 treatment가 취해지지 않은 경우 입니다. 위의 태블릿 예제에서는 $E[Y_0|T=0] < E[Y_0|T=1]$이기 때문에 Bias가 발생합니다. 즉, 태블릿을 제공할 수 있는 학교는 태블릿 제공에 관계없이 그렇지 않은 학교보다 학생들의 성적이 좋기 때문입니다.

그럼 왜 이런일이 발생할까요? 이후 포스트에서 교란자(Confounder)에 대해 다룰 것이지만, 대략적으로 설명하면 우리가 제어할 수 없는 요인들이 treatment와 종속되어있기 때문에 이러한 편향이 발생합니다. 인과관계의 측정을 더욱 정확히 하려면 이러한 외부요인(등록금, 교사의 능력 등)을 철저히 비슷한 수준으로 통제해야 합니다.

즉, $E[Y_0|T=0] = E[Y_0|T=1]$이라면 연관성은 인과성과 같습니다!

$\;$

다시 한번 수식을 통해 설명하면

$E[Y|T=1] - E[Y|T=0] = E[Y_1 - Y_0|T=1] = ATT$

이고

$E[Y_0|T=0] = E[Y_0|T=1]$

이기 때문에

$E[Y_1 - Y_0|T=1] = E[Y_1|T=1] - E[Y_0|T=1]\\\hspace{26.8mm}= E[Y_1|T=1] - E[Y_0|T=0] = E[Y|T=1] - E[Y|T=0]$

또한, 간단히 계산해보면 $E[Y_1 - Y_0|T=1]=E[Y_1 - Y_0|T=0]$임을 얻을 수 있기 때문에 이를 통해서

$E[Y|T=1] - E[Y|T=0] = ATT = ATE$

입니다! 즉, 해당 값의 차이를 통해 인과적 효과를 얻을 수 있습니다.

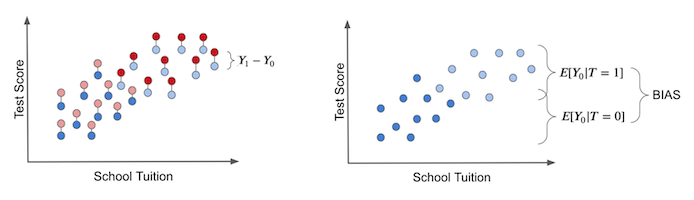
다시 한번, 예제를 통해 설명해보면, treatment 그룹과 그렇지 않은 그룹의 단순 평균만을 비교하면 아래 그림과 같습니다.

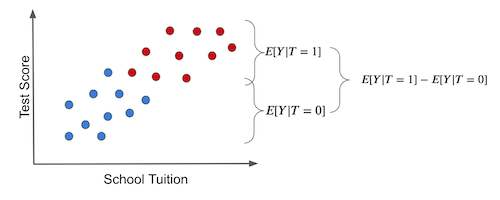
두 그룹간 차이는 다음과 같은 두 가지 원인을 가질 수 있습니다.

1. treatment의 효과로 시험 점수가 상승하였다.

2. treatmet자체가 아닌 그룹간의 차이로 인해 상승하였다. 이 경우에는 treatment를 받은 학생과 그렇지 않은 학생보다 더 높은 등록금을 낸다는 차이가 있습니다. 즉 성적의 차이 중 일부는 등록금이 교육자체에 영향을 주기 때문일 수도 있습니다.

진짜 treatment의 효과는 이제 아시다 시피 전지전능한 능력이 있어야 알 수 있습니다. 아래의 그림은 그러한 슬픈 사실을 잘 보여주고 있습니다!! 여기서 연한색으로 표시된 점은 잠재적 효과를 나타냅니다.

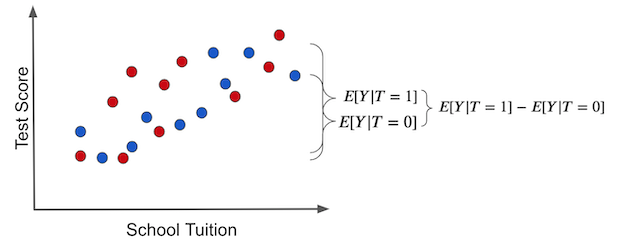
만약 가상의 상황에서, 태블릿이 학교에 무작위로 할당되었다고 해봅시다. 그럼 모든 학생에게 태블릿을 받을 기회가 있고, treatment는 아래의 그림과 같이 모든 등록금에 대해 잘 분배되어 나타날 것입니다.

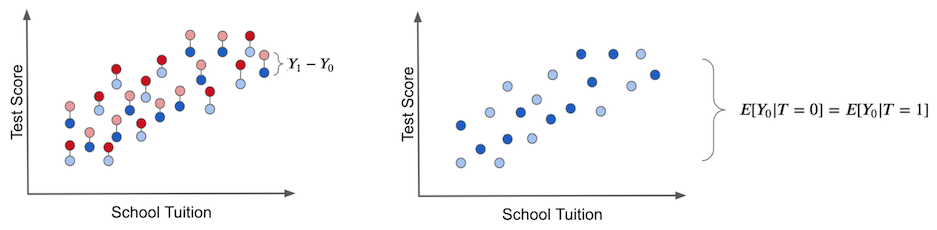
이 경우, 위에서 다루었듯이 실험군과 대조군의 차이는 ATE입니다! 이는 treatmemt와 연관되어 있는 다른 요인이 없기 때문입니다.

결론

이것이 바로 인과추론의 핵심입니다. Bias를 제거하고 treatment를 받은 사람과 그렇지 않은 사람을 비교할 수 있는 방법을 찾는 것입니다. 이를 통해, 두 그룹 평균의 차이로 ATE를 얻는 것입니다! 이 글의 작성자는 "Ultimately, causal inference is about figuring out how the world really works, stripped of all delusions and misinterpretations." 라고 표현을 해주었는데요. 인과 추론은 정말 치밀하게 접근해야할 것 같습니다..!