[Causal Inference] Doubly Robust Estimation

Introduction

Confounder 가 존재하는 경우 Causal Effect, 즉, ATE를 추정하기 위해 잘 알려진 방법이 있습니다. Propensity score weighting, Linear Regression을 이용하는 방법 등이 있습니다. 여기서 Linear Regression을 이용하는 방법은

를 추정하는 방법입니다. 그럼 여기서 Propensity score weighting 는 무엇일까요?

Propensity Score

ATE 를 추정하기 위해 Confounder 인 $X$를 제어해주어야 합니다. 즉, $(Y_1, Y_0 ) \perp T \mid X$가 되도록 해주어야 합니다. 하지만 여기서 밸런싱 스코어를 제어하는 것만으로 충분하다고합니다! 여기서 나온 것이 Propensity Score 입니다. 이것은 $P(T\mid X) = P(x)$ 으로 조건부 Treatment 확률입니다. 즉,

이 만족된다고 합니다. 이를 도식화하면 아래와 같습니다!

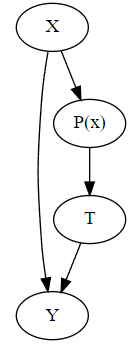
Propensity Weighting

자, 그럼 성향 점수를 어떻게 이용할까요? 성향 점수를 이용해 다음과 같이 ATE를 추정할 수 있습니다.

Treatment에 대한 확률 값으로 나누어 주는 것입니다. 이러한 스케일링의 효과는 인과효과의 밸런스를 맞추어주는 효과가 있습니다 다음의 사진처럼 말이죠 !!

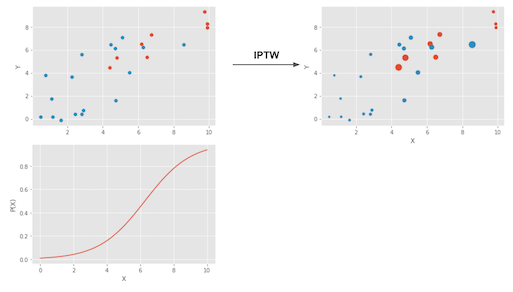
이러한 방법은 Inverse Probability of Treatment Weighting (IPTW) 이라고 부릅니다! 그리고 다음과 같이 축약된 형태로 나타낼 수 있습니다.

그럼 여기서 Propensity Score의 추정은 어떠한 방법으로 할까요? 일반적으로 logistic regression 방법을 이용한다고 합니다. 예측력이 좋은 ML방법도 있습니다만, 그렇게 권장되지 않는다고 합니다. 그 이유는 Propensity Score의 핵심은 경향성을 통해 균형을 찾는 것이기 때문에 예측자체에 초점이 맞추어 져있는 ML방법은 적절하지 않다고 합니다!

Propensity Score에 대한 더 자세한 설명은 여기를 참고하세요!

Doubly Robust Estimation

그럼 Doubly Robust Estimation은 무엇일까요? 이름만 보면 이중 강건 추정.. 이중으로 Robust 추정을 할 것같은데요..! 그것이 맞습니다! 간략하게 소개하면 ATE를 추정하는 방법 중 하나인데요! 어떠한 방법으로 이중 Robust 추정이 가능한지 알아보기 위해 아래의 Doubly robust estimation 식부터 살펴보며 얘기하여보겠습니다.

여기서 $\hat{P}(X_i)$ 는 Propensity score의 추정치이며, $\hat{\mu}_j(X_i)$ 는 $E[Y\mid X, T = j]$ 의 추정치 입니다.

위 식에서 앞쪽의 항은 $E[Y_1]$, 뒤쪽의 항은 $E[Y_0]$에 대한 추정입니다.

그럼 이 방법을 Athey and Wager, Estimating Treatment Effects with Causal Forests: An Application에서 제공하는 시뮬레이션 데이터에 적용해보겠습니다.

import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import seaborn as sns

from sklearn.linear_model import LogisticRegression, LinearRegression

from joblib import Parallel, delayed # for parallel processing


style.use("fivethirtyeight")
pd.set_option("display.max_columns", 6)

data = pd.read_csv("C:/CausalInference/learning_mindset.csv")
categ = ["ethnicity", "gender", "school_urbanicity"]
cont = ["school_mindset", "school_achievement", "school_ethnic_minority", "school_poverty", "school_size"]

data_with_categ = pd.concat([
    data.drop(columns=categ), # dataset without the categorical features
    pd.get_dummies(data[categ], columns=categ, drop_first=False) # categorical features converted to dummies
], axis=1)



def doubly_robust(df, X, T, Y):
    ps = LogisticRegression(C=1e6, max_iter=1000).fit(df[X], df[T]).predict_proba(df[X])[:, 1]
    mu0 = LinearRegression().fit(df.query(f"{T}==0")[X], df.query(f"{T}==0")[Y]).predict(df[X])
    mu1 = LinearRegression().fit(df.query(f"{T}==1")[X], df.query(f"{T}==1")[Y]).predict(df[X])
    return (
        np.mean(df[T]*(df[Y] - mu1)/ps + mu1) -
        np.mean((1-df[T])*(df[Y] - mu0)/(1-ps) + mu0)
    )

T = 'intervention'
Y = 'achievement_score'
X = data_with_categ.columns.drop(['schoolid', T, Y])

doubly_robust(data_with_categ, X, T, Y)

np.random.seed(88)
# run 1000 bootstrap samples
bootstrap_sample = 1000
ates = Parallel(n_jobs=4)(delayed(doubly_robust)(data_with_categ.sample(frac=1, replace=True), X, T, Y)
                          for _ in range(bootstrap_sample))
ates = np.array(ates)

print('Score :%3f' % doubly_robust(data_with_categ, X, T, Y))
sns.distplot(ates, kde=False)
plt.vlines(np.percentile(ates, 2.5), 0, 20, linestyles="dotted")
plt.vlines(np.percentile(ates, 97.5), 0, 20, linestyles="dotted", label="95% CI")
plt.title("ATE Bootstrap Distribution")
plt.legend();

위 결과 ATE의 추정치는 0.3882이며 Bootstrap 방법을 이용한 95% 신뢰구간은 (0.3536, 0.4197)입니다.

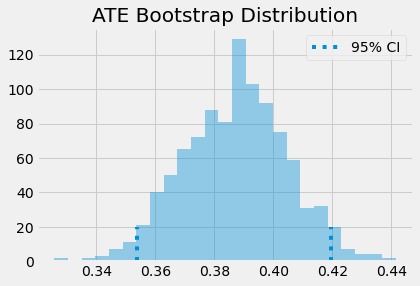
그럼 이때 Propensity Score 추정이 좋지 못한 경우를 가정해봅시다. 그러한 경우 ATE의 추정치는 어떻게 될까요?

def doubly_robust_wrong_ps(df, X, T, Y):
    # wrong PS model
    np.random.seed(654)
    ps = np.random.uniform(0.1, 0.9, df.shape[0])
    mu0 = LinearRegression().fit(df.query(f"{T}==0")[X], df.query(f"{T}==0")[Y]).predict(df[X])
    mu1 = LinearRegression().fit(df.query(f"{T}==1")[X], df.query(f"{T}==1")[Y]).predict(df[X])
    return (
        np.mean(df[T]*(df[Y] - mu1)/ps + mu1) -
        np.mean((1-df[T])*(df[Y] - mu0)/(1-ps) + mu0)
    )

print('Score %3f' % doubly_robust_wrong_ps(data_with_categ, X, T, Y))


np.random.seed(88)
parallel_fn = delayed(doubly_robust_wrong_ps)
wrong_ps = Parallel(n_jobs=4)(parallel_fn(data_with_categ.sample(frac=1, replace=True), X, T, Y)
                              for _ in range(bootstrap_sample))
wrong_ps = np.array(wrong_ps)

print(f"Original ATE 95% CI:", (np.percentile(ates, 2.5), np.percentile(ates, 97.5)))

print(f"Wrong PS ATE 95% CI:", (np.percentile(wrong_ps, 2.5), np.percentile(wrong_ps, 97.5)))

Propensity Score 추정값은 0.1과 0.9사이의 임의의 값을 적용하여 위와 같이 Doubly robust estimation을 얻어보면 0.3801이며, Bootstrap을 이용한 95% 신뢰구간은 (0.3385, 0.4328)입니다. 거의 비슷하게 추정하였으며, 신뢰구간은 조금 더 넓어지는 경향을 보이네요!

자, 그럼 다음으로 $\mu(X_i)$의 추정이 좋지 못한 경우를 살펴보겠습니다.

def doubly_robust_wrong_model(df, X, T, Y):
    np.random.seed(654)
    ps = LogisticRegression(C=1e6, max_iter=1000).fit(df[X], df[T]).predict_proba(df[X])[:, 1]
    
    # wrong mu(x) model
    mu0 = np.random.normal(0, 1, df.shape[0])
    mu1 = np.random.normal(0, 1, df.shape[0])
    return (
        np.mean(df[T]*(df[Y] - mu1)/ps + mu1) -
        np.mean((1-df[T])*(df[Y] - mu0)/(1-ps) + mu0)
    )

print('Score %3f' % doubly_robust_wrong_model(data_with_categ, X, T, Y))

np.random.seed(88)
parallel_fn = delayed(doubly_robust_wrong_model)
wrong_mux = Parallel(n_jobs=4)(parallel_fn(data_with_categ.sample(frac=1, replace=True), X, T, Y)
                               for _ in range(bootstrap_sample))
wrong_mux = np.array(wrong_mux)

print(f"Original ATE 95% CI:", (np.percentile(ates, 2.5), np.percentile(ates, 97.5)))
print(f"Wrong Mu ATE 95% CI:", (np.percentile(wrong_mux, 2.5), np.percentile(ates, 97.5)))

$\mu(X_i)$의 추정값을 $N(0,1)$에서 임의로 추출하여 적용하여 위와 같이 Doubly robust estimation을 얻어보면 0.3981이며, Bootstrap을 이용한 95% 신뢰구간은 (0.3387, 0.4197)입니다. 위의 정상적인 추정값보다 조금 벗어났지만 큰 수준은 아닌것 같네요, 신뢰구간은 조금 더 넓어졌습니다.

자! 그럼 어떤 느낌인지 아시겠나요? Propensity Score 와 Confounder를 regression하여 얻은 $\mu(X_i)$값 중 하나만 올바르게 추정되더라도 준수한 추정을 해낼 수 있습니다. 물론 잘못된 추정으로 인한 불확실성때문에 추정치의 분산이 커지긴하지만요..!

출처: https://matheusfacure.github.io/python-causality-handbook/12-Doubly-Robust-Estimation.html