안녕하세요!
오늘은 Instrumental Variable에 대해 공부해본 내용을 포스팅해보겠습니다!!
Introduction
Instrumental Variable은 이름에서와 알 수 있듯이 계측기 변수라는 뜻으로, 정확한 계측을 도와주는 변수를 말하는데요! 천천히 알아가보겠습니다.
자 다음과 같은 상황을 가정해보겠습니다.
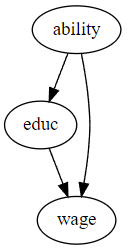
저희는 교육에 대한 임금의 효과를 측정하고자 합니다. 하지만 개인의 능력이라는 Confounder가 존재합니다.. 자, 전의 포스팅에서도 배웠다 싶이 이러한 경우에 교육에 대한 임금의 효과는 편향되게 됩니다. 이러한 경우 간단하게 개인의 능력을 조건화하여 해결할 수 있습니다! 하지만, 개인의 능력을 정량화하기 힘든 경우, 즉 이를 조건화할 수 없는 경우에 어떻게 해야할까요?
Instrumental Variables
위와 같이 막막한 경우에 Instrumental variable을 이용하면 해결할 수 있습니다!

여기서 임금을 , 교육을 , 개인의 능력을 , Instrumental variable을 라고 하겠습니다.
그럼 각 특성들 간에 다음과 같은 식이 성립합니다.
우리가 원하는 것은
로 두고 를 측정하는 것입니다. 하지만 여기서 와 는 서로 독립적이지 않기 때문에 불가능합니다..
자 그럼 instrumental variable과 임금간의 공분산을 한번 계산해보겠습니다.
입니다. (여기서 은 independent 에러로 가정합니다.)
위 식을 다시 한번 의 식으로 나타내면
입니다. 여기서 재밌는 것은 는 에 대한 의 회귀 계수입니다.
그럼 여기서 Confounder를 고려하지 않고 두번의 회귀모형적합으로 우리가 원하는 교육에 대한 임금의 효과 를 추정할 수 있다는 것입니다!
이때 는 1st Stage, 는 Reduced Form이라고 하겠습니다.
예제: 출생 분기와 교육이 임금에 미치는 영향
미국에서 입학하는 해의 1월 1일까지 6세가 되어야 학교에 입학할 수 있습니다. 하지만 법은 16세까지 학교를 의무적으로 다닐 것을 요구하고, 이때 법적으로 자퇴가 허용된다고 합니다. 그 결과 연말에 태어난 사람이 연초에 태어난 사람들 보다 평균적으로 더 많은 교육을 받게 됩니다.

이때 개인의 능력과 출생은 서로 독립적이라고 가정된다면 출생분기는 instrumental variable로 이용될 수 있습니다.
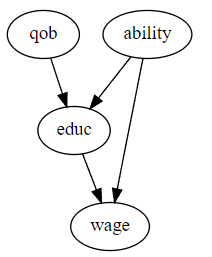
1st Stage
우선 유효한 instrumental variable인지 알아보기 위해 두가지 가정을 확인하여야 합니다.
-
, 강력한 1st Stage 효과를 가지며, instrumental variable이 Treatment 변수에 직접 영향을 주고 있음을 의미합니다.
-
. instrumental variable이 Treatment에 만 직접적으로 관여하며 목표 변수인 에는 를 거쳐야만 영향을 미친다는 것입니다.

위 플롯에서와 같이 출생 분기별로 교육수준에 차이가 나타남을 확인할 수 있었고, 예시를 단순화하기 위해 Q4만을 더미 변수로 이용해 instrumental variable로 활용해 보겠습니다.

이를 이용해 회귀모형을 적합하여본 결과 Treatment에 대한 Q4의 효과는 0.1로 추정되었으며 p-value 또한 굉장히 낮음을 확인할 수 있었습니다.
Reduced Form
위에서 언급되었던 instrumental variable의 두번째 조건은 확인하기 어려우며, 우리들 각자의 삶의 경험을 통한 사전정보 (?) 를 통해 맞다고 가정을 하고 진행하겠습니다. (통계적 검증은 어렵지만 굉장히 합리적인 가정이라는 의미입니다..)
그 결과 
Q4에 대한 회귀 계수 값은 0.008 이며 p-value 또한 낮은 값으로 위 추정치가 유의미함을 보여주고 있습니다!!
자 그럼 1st Stage 값과 Reduced Form의 값을 모두 얻었습니다. 계산 결과를 바탕으로 ATE를 구하여 보면 0.08임을 얻을 수 있습니다. 여기서 임금의 로그값을 이용하여
계산하였으니 교육의 연단위 효과는 약 8%임을 알 수 있습니다.
Weakness of Instruments
Instrumental variable을 이용할 때 ATE를 간접적으로 추정하게 됩니다. 결과 변수에 대한 Treatment의 영향이 강한것도 중요하지만, Instrumental variable과 Treatment가 약한 상관관계를 가지는 경우에 ATE의 추정에 대한 분산이 커지게 됩니다.
그럼 이를 알아보기 위해 시뮬레이션을 해보겠습니다.
여기서
즉, 는 Confounder, 는 Treatment, 는 outcome, 는 instrumental 변수입니다.
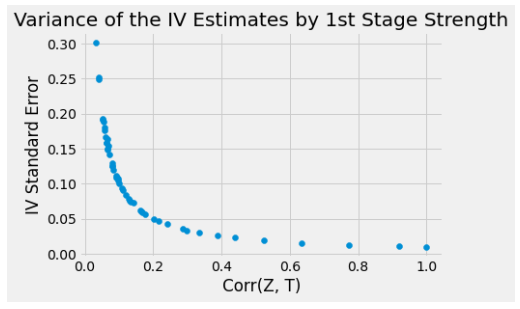
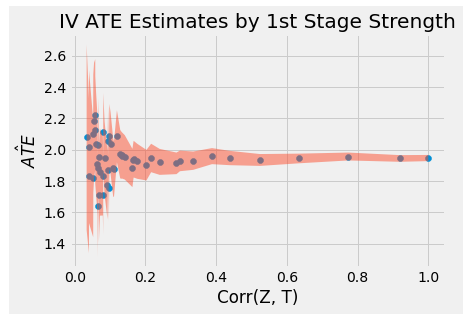
여기서 그림을 보시면 Instrumental 변수가 Treatment와 상관계수가 높을수록 ATE추정치의 분산이 줄어드는 것이 확인됩니다.
실제로 IV의 ATE 추정은 조금 편향되어 있는 것을 확인할 수 있는데
이것은 IV를 이용한 방법이 OLS 의 편향을 받기 때문이라고 설명하고 있습니다.
하지만 제생각에는 처음 시뮬레이션 셋팅에서 T -> Z로의 인과적관계에서 Z 와 U의 상관관계가 커지기 때문에 IV의 두번째 가정에 위배되기 때문에 그러한 편향이 생긴다고 생각됩니다. 아무래도 Correlation 을 1까지 올리기 위함인것 같지만 셋팅을 바꾸어 본다면 더욱 유의미하지 않을까 싶네요.
그래서 이 셋팅을 Z->T로 바꾸어 보았습니다.
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import pandas as pd
np.random.seed(12)
n = 10000
U = np.random.normal(0, 2, n)
stddevs = np.linspace(0.1, 100, 50)
Z = np.random.normal(1, 0.5, n)
Ts = {f"T_{z}": np.random.normal(1 +0.5*U +Z, s, n) for z, s in enumerate(stddevs)}
Ys = {f"Y_{i}": np.random.normal(2 + 0.5*U + 2*Ts[f"T_{i}"], 5, n) for i in range(50)}
sim_data = pd.DataFrame(dict(U=U, Z=Z)).assign(**Ts).assign(**Ys)
LR = LinearRegression()
temp = []
for i in range(50):
LR.fit(sim_data[[ 'Z'] ], sim_data['Y_'+str(i)])
second = LR.coef_[0]
LR = LinearRegression()
LR.fit(sim_data[['Z']], sim_data['T_'+str(i)])
first= LR.coef_[0]
temp.append(second/ first)
plt.plot(temp[::-1])
plt.hlines(2, xmin= 0 , xmax= 50)왜 저자가 저렇게 셋팅했던것인지 알 수 있을 정도로 극단적인 셋팅이긴 하나...
바꾸어 진행해보니 실제로 편향이 거의 없는 듯해보이네요 .
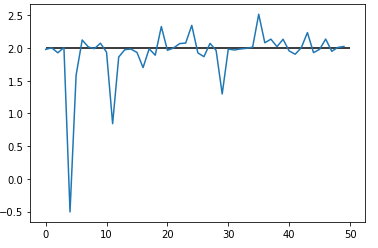
- 플롯에서 X 축이 0 -> 50 으로 갈수록 Correlation 이 커지고 ( 전의 셋팅처럼 1에 가깝게 커지지 않습니다. 대략 0.5 정도 까지 상승합니다.), y 축은 ATE추정치를 말합니다.
어쩃든 중요한 것은 가정에 아주 잘 맞는 Instrumental variable 을 이용한다면 ATE 를 정확히 추정할 수 있습니다!!
