[Reinforcement Learning] DQN 리뷰

안녕하세요 오늘은 지난번에 공부했던 Playing Atari with Deep Reinforcement Learning라는 논문에 대해 리뷰해 보겠습니다. 해당 논문에서 소개하는 알고리즘은 DQN(Deep Q-Network)으로 딥러닝과 기존의 강화학습 방법인 Q-Learning을 결합한 방법이라고 보시면 될 것 같습니다! 본 리뷰는 DQN알고리즘을 좀 더 이해해보고자 작성하였으며 related work와 자세한 experiment는 생략하겠습니다!

저는 이쪽 공부를 한번도 해 본적없지만, 강화학습이 너무 궁금해서 이 논문을 읽어봤는데 너무 재밌게 잘 읽어서 리뷰를 해 보았습니다. 이 논문을 보면서 Q-learning을 처음 접해보았는데 비교적 오래된 아이디어임에도 불구하고 꽤 흥미로우니 리뷰 보시고 논문도 꼭 찾아보시길 바랍니다.

1. Introduction

Problem

• 시각, 음성과 같은 고차원 입력데이터를 통해 학습하는 것은 강화 학습의 오랜 과제였고 이에 대한 성능은 높은 품질의 특성에 매우 의존하였다.
• 딥러닝의 관점에서의 강화학습의 어려움은 두 가지로 언급된다.
  - 대용량의 직접 라벨링된 트레이닝 데이터가 필요함. 하지만 강화학습에서는 희박하고 노이즈가 많으며 딜레이가 존재하는 reward가 발생하여 학습에 어려움이 있다.
  - 많은 딥러닝 알고리즘들이 데이터가 서로 독립이라고 가정하지만, 강화학습에서는 일련의 상태들이 서로 매우 관련(highly correlated)되어 있다.

Contribution

• raw video 데이터에서 CNN(Convolutional nueral network)를 이용하여 성공적으로 컨트롤 정책을 학습하였다.
• Q-learning 알고리즘을 적용하여 네트워크를 학습하였다.
• 데이터의 강력한 종속성을 극복하기 위해 Experience replay 메커니즘을 이용하여 이전의 트랜지션들을 랜덤하게 사용하였고 결과적으로 많은 과거 데이터의 학습분포를 매끄럽게 하였다. (일련의 과정들을 순차적으로 이용하지 않고 이를 저장해두고 랜덤하게 이용하였다고 보시면 될 것 같습니다.)

2. Background

• 여기서 저자는 환경 $\Epsilon$ 과 상호작용하는 에이전트(agent)를 고려하였습니다.
  - 매 스텝마다 액션$a_t$을 선택하여 취하고 이에 따라 state와 rewards은 얻게 됩니다.
  - 해당 논문에서는 Atari2600 게임들을 이용해서 게임을 통해 관측가능한 이미지 $x_t$를 관측하고 이에 따른 보상인 $r_t$를 얻게됩니다.
  
• agent가 게임의 화면만을 관측하여 현재의 상황을 완전히 이해하는 것은 거의 불가능에 가깝습니다. 그래서 저자는 action과 observation의 시퀀스인 $s_t = x_1, a_1, x_2,..., a_{t-1}, x_t$를 고려하였다고 합니다. 여기서 이 시퀀스를 유한한 시간으로 제한합니다. 이러한 시퀀스는 time-step에 의존하면서 크고 유한한 MDP(Markov decision process)를 구성할 수 있다고 합니다.

Reward

• 이 agent의 목표는 현재뿐만아닌 행동으로 인한 미래의 reward가 가장 높은 action을 선택하는 것입니다.

• 해당 논문에서 저자는 미래의 reward인 $R_t$에 대해서는 조금의 할인(?)을 적용하며 이에 대한 식은 아래와 같습니다.

  $\hspace{50mm}R_t = \sum_{t'=t}^T \gamma^{t'-t}r_{t'}$

  여기서 $\gamma$는 할인율(?)이며 해당 시점부터 미래에 대한 시점의 reward를 점점 낮을 값을 주어 계산합니다.

  이 이유에 대해 개인적으로 생각해보면, 저희가 직접 게임을 하게 되더라도 너무 먼 미래까지 생각하면 게임이 지나치게 어려워진다 생각이 듭니다. 마찬가지로 이 agent를 학습할 때에도 할인율을 적용하지 않으면 현재 어떠한 액션을 취해야하는지 결정이 어려울 것으로 보입니다.

Action-value function

• Optimal action-value function $Q^*(s,a)$ : 어떠한 전략을 따른 뒤에 시퀀스 s를 통해 어떠한 액션 a 취한 후 달성할 수 있는 기대 return의 최대값.
  즉,

  $\hspace{30mm}Q^*(s,a) = max_\pi \mathbb{E}[R_t\mid s_t=s, a_t=a,\pi]$

  여기서 $\pi$는 시퀀스로부터 액션으로 매핑되는 정책/전략 입니다.(또는 액션에 대한 분포)
  

• 이 optimal action-value function은 Bellman equation과 같습니다.
  - Bellman equation을 통해서 다음 time-step에서의 s'에 대해 $Q^*(s',a')$가 모든 가능한 액션 $a'$에 대해 알려져 있다면, 최적 전략은 $r+\gamma Q^*(s',a')$의 기대값을 최대로하는 $a'$를 선택하는 것입니다.
  즉, 아래와 같은 식이 성립하게 됩니다.

  $\hspace{28mm}Q^*(s,a) = E_{s'\sim\epsilon}\left[r+ \gamma max_{a'}Q^*(s',a')\mid s,a\right]$

• 많은 강화 학습 알고리즘의 기본 아이디어는 이 action-value function을 추정하는 것으로 iterative update를 Bellman equation에 적용합니다.

  $\hspace{28mm}Q_{i+1}(s,a) = E_{s'\sim\epsilon}\left[r+ \gamma max_{a'}Q_{i}(s',a')\mid s,a\right]$

  이러한 value interation알고리즘을 적용하면 optimal action-value function은 수렴 하게됩니다.

  $\hspace{45mm}Q_i \rightarrow Q^* \;\;as\;\; i \rightarrow \infty$

  해당 논문에서는 이 optimal action-value function을 근사하기 위해 neural network를 이용합니다.

• 해당 논문에서는 이 neural net work를 Q-network라고 합니다. 이 Q-network는 다음과 같은 loss function $L_i(\theta_i)$를 최소화하며 학습합니다.

  $\hspace{35mm}L_i(\theta_i) = \mathbb{E}_{s,a\sim \rho(\cdot)}\left[(y_i - Q(s,a;\theta_i))^2\right]$

  여기서 $y_i$는 $E_{s'\sim\epsilon}\left[r+ \gamma max_{a'}Q_{i}(s',a'; \theta{i-1})\mid s,a\right]$이고, $\rho(s,a)$는 s와 a에대한 확률 분포로 행동 분포입니다. 해당 논문에서는 SGD를 이용해 weight $\theta_i$를 최적화 합니다.

3. Deep Reinforcement Learning

해당논문의 목적은 RGB데이터에 작동하고 SGD를 통해 효율적으로 학습데이터를 처리하는 딥러닝 신경망을 강화 학습알고리즘에 연결하는 것이라고 합니다.

저자가 이 섹션에서 강조하는 부분은 Replay Memory으로, 제가 이해하기에도 이 알고리즘의 성공에 가장 큰 요인이라고 생각되는 부분입니다.

Algorithm

• 우선 $N$개의 트랜지션을 저장할 수 있는 replay memory $\mathcal{D}$와 action-value function $Q$의 weight를 랜덤으로 초기화 합니다.

• 각 에피소드 (한번의 게임 실행)에서 시간에 지남에 따라 관측치를 s_t에 저장합니다. (s_t의 구성은 위에서 언급되었습니다.) 여기서 $\phi$는 모두 다른 길이를 가진 상태 시퀀스인 $s_t$를 고정된 길이로 변환하여 주는 함수 입니다.
  - 해당 논문에서는 최근 4개의 관측치를 순차적으로 $s_t$에 저장하는데 이는 이미지를 통해 게임을 보았을 때 한장의 사진으로만 게임의 진행을 파악하기 어렵기 때문인 것으로 생각됩니다. 즉,벽돌 부수기 게임에서 최근 4장의 이미지를 통해 공이 위로향하는지 아래로 향하는지 판단하기 위함으로 추측됩니다!

• $\epsilon$- policy를 통해 액션을 선택합니다.
  - 여기서 $\epsilon$- policy란 $\epsilon$의 확률로 랜덤한 액션을 선택하거나 1-$\epsilon$의 확률로 $Q$ function이 가장 큰 값을 갖는 액션을 선택하는 것으로 $\epsilon$값을 시간이 지남에 따라 감소시키며 최적의 $Q$ function이 되기까지 여러 action을 통해 $Q$ function값을 최적화 하기 위함으로 보입니다.

• 게임(emulator)를 통해 다음 스텝의 리워드 $r_{t+1}$과 다음 관측치 $x_{t+1}$을 얻어 새로운 상태 $s_{t+1}$을 업데이트 합니다.

• 매 스텝마다 agent의 경험을 Replay memory $\mathcal{D}$에 저장합니다. ( $e_t = (s_t, a_t, r_t, s_{t+1})$ )

• 알고리즘이 각 에피소드의 매 시간마다 replay memory 에서 임의로 표본을 추출하고 minibatch update를 실행합니다. (해당 섹션에 설명되어있지 않지만 충분한 데이터가 Replay memory에 있지 않은 경우 업데이트는 스킵합니다.)
  - 여기서 minibatch update의 target은
  
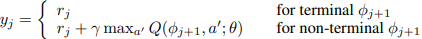
  으로 직전 시점의 최대 Q값에 $\gamma$를 곱하여 현재 시점의 reward와 더해 준 값이며, 게임이 마지막인 경우 현재 시점의 reward만을 계산하여 줍니다.

알고리즘의 목적은 이렇게 재귀적으로 $Q$ 함수의 값을 계산하고 업데이트 해가며 최적의 $Q$ 함수를 찾아내는 것이 목적입니다.

Summary

• 제 생각으로 논문의 가장 큰 기여점은 아래와 같은 두가지가 될 것으로 보입니다.
  - Deep neural network와 Q-Learing 알고리즘의 연결
  - Replay Memory 전략을 통해 관측치의 상관성을 줄이고 효율적으로 minibatch update를 진행

• 이 알고리즘의 핵심은 최적의 action-value function $Q$를 찾아가는 과정으로 discount factor $\gamma$를 적용하여 단기적인 이득뿐만아니라 현재의 action으로 인해 가까운 미래의 reward를 최대화하는 action를 찾도록한다.

• 리뷰에는 언급하지 않았지만 다들 아시다시피 이 알고리즘은 Atari 게임들에서 아주 성공적인 성능을 보여주었다고 합니다.

해당 논문은 이후에 많은 Double-DQN, Dueling-DQN 등으로 많은 개선버전이 존재하며, 최근에 이러한 개선버전을 다량 적용한 Rainbow알고리즘이 굉장히 유명한 것으로 알고 있습니다. 저도 이에 대해 계속 공부 중이며 관련 논문들을 찾아보시면 굉장히 재밌을 것 같네요!

현재 강화학습 알고리즘을 통해서 개인 프로젝트를 진행하고 있는데 조금 정리가되면 코드 정리해서 첨부할 수 있도록 하겠습니다!

감사합니다.