🚩딥러닝 기초 - part10. Batch Gradient Descent .vs Stochastic Gradient Descent

🟢 Introduction

이전 part06에서 gradient descent에 대해서 학습했었다.
그리고 선형일때(linear regression)과 비 선형 그래프(logistic regression)또한 알아보았다.
선형의 모형은 예측을 위해 사용이되고, logistic의 경우 분류에 사용이 되었다.
둘 다 최적의 모델 $y=wx+b$, $1\over 1+e^{-k}$$(k = wx+b)$ 을 구하기 위하여 gradient descent를 수행하였다.
(모델의 오차를 잘 표현할 수 있는 오차함수를 정의하고, 해당 오차함수를 미분해서 얻은 기울기 값을 빼는 형식으로 경사하강을 수행 - 파라미터를 업데이트)

하지만 이런 경사하강법에도 여러 방법이 있다는 것을 아는가?

이제 gradient descent의 방법의 2가지에 대해서 배워보자.

Batch Gradinet Descent

"비용함수"를 편미분하여 나온 값을 통해 파라미터의 값을 업데이트 할 수 있었다.
(여기서의 비용함수는 Linear regression / rogistic regression인가에 따라서 달라질 것이다)

이 때 우리는 "비용함수"를 사용했다.
즉, "평균"제곱오차가 바로 비용함수였다.
평균제곱오차라는 건 모든 입력 데이터에 대한 오차 제곱의 평균이라는 말이다.

왜이렇게 단순한 말을 강조할까? 중요해서 그렇다.

비용함수와, 손실함수에 대해서 기억나는가?

• 손실함수는 데이터 하나 대한 오차를 구하는 함수이고
• 비용함수는 이러한 손실함수로 구해진 오차들의 평균이다.

지금까지는 쭉 설명한 내용은 "비용함수"를 사용했기에 모든 데이터에 대한 오차를 구한 다음 이를 업데이트(파라미터의 갱신)에 반영을 했다는 의미이다.

이렇게 비용함수로 gradient descent를 수행하는 것이
Batch gradient descent라고 한다.

딥러닝에서 모든 학습데이터를 전부 보는 것을 한 세대라고 표현하는데 즉, Batch gradient descent는 한 세대마다 파라미터의 갱신이 이루어지는 것이다.

Batch gradient descent 과정

• 비용함수

  $\mathcal{J} = \frac{1}{2n} \sum_{i=1}^N (\hat{y}^{(i)} - y^{(i)})^{2} = \frac{1}{2n} \sum_{i=1}^N ((w x^{(i)}+b) - y^{(i)})^{2}$

• $w,b$에 대한 편미분(partial derivative)

  $\frac{\partial \mathcal{J}}{\partial w} = \frac{1}{n} \sum_{i=1}^N (\hat{y}^{(i)} - y^{(i)}) x^{(i)}$
  $\frac{\partial \mathcal{J}}{\partial b} = \frac{1}{n} \sum_{i=1}^N (\hat{y}^{(i)} - y^{(i)})$

• Gradient descent method (파라미터 업데이트)

  $w := w - \alpha \frac{\partial \mathcal{L}^{(i)}}{\partial w} = w - \alpha \frac{1}{n} \sum_{i=1}^N (\hat{y}^{(i)} - y^{(i)}) x^{(i)}$
  $b := b - \alpha \frac{\partial \mathcal{L}^{(i)}}{\partial b} = b - \alpha \frac{1}{n} \sum_{i=1}^N (\hat{y}^{(i)} - y^{(i)})$

Stochastic Gradient Descent (SGD)

그럼 Stochastic Gradient Descent (SGD)는 무엇일까?

눈치챘는가? 비용함수가 아닌 손실함수를 기준으로 파라미터를 업데이트 하는 것이다.

각 샘플(학습데이터)마다 구해진 ($오차^2$)를 기반으로 즉시 파라미터를 업데이트 하게 된다.

모든 샘플의 loss에 대해서 전부 각각의 파라미터의 갱신이 이루어 진다.

예를 들어 입력데이터의 개수가 100개라면 1세대(100개)동안 100번의 파라미터 갱신이 이루어 지는 것이다. (batch의 경우 1번이었음)

이렇게 되면 뭐가 다른걸까?

바로바로 갱신하다보니 loss가 빠르게 감소할 수 있다. 하지만 전체 데이터의 오차를 반영한 것이 아니므로 이러한 감소가 최적의 방향으로 흘러가는 것인지는 알 수 없다.

따라서, 항상 빠른 수렴을 한다라고는 정의할 수 없다.

SGD 과정

• 손실함수

  $\mathcal{L}^{(i)} = (\hat{y}^{(i)} - y^{(i)})^{2} = ((w x^{(i)}+b) - y^{(i)})^{2}$

• $w,b$에 대한 편미분(partial derivative)

  $\frac {\partial \mathcal{L}^{(i)}}{\partial w} = 2x^{(i)}(\hat{y}^{(i)} - y^{(i)})$
  $\frac{\partial \mathcal{L}^{(i)}}{\partial b} = \hat{y}^{(i)} - y^{(i)}$

• Gradient descent method (파라미터 업데이트)

  $w := w - \alpha \frac{\partial \mathcal{L}^{(i)}}{\partial w} = w - 2\alpha x^{(i)}(\hat{y}^{(i)} - y^{(i)})$
  $b := b - \alpha \frac{\partial \mathcal{L}^{(i)}}{\partial b} = b - 2\alpha (\hat{y}^{(i)} - y^{(i)})$

참고

왜 SGD에서는 Weight및 Loss의 변화가 두께가 있는 그래프처럼 보일까?

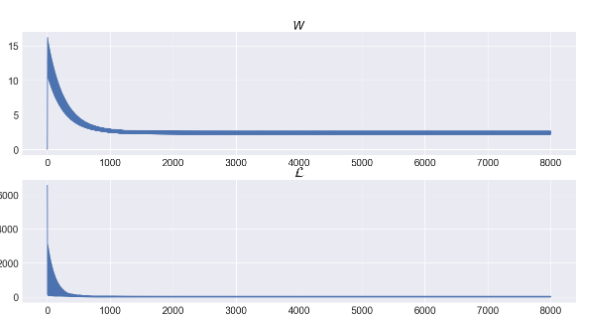
샘플마다 시행되므로 최적의 방향을 찾기위해서 값이 진동하는 것처럼 보이므로 두께가 있는 것과 같이 그래프가 보인다.