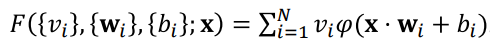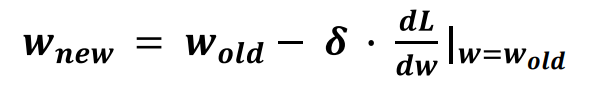Universial Function Approximator

• 보편 함수 f의 근사 모델 F 를 경사하강을 통해 적당한 모델 parameter vi, wi, bi 구한다.
  

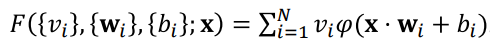
step 0. 필요 라이브러리 import

import matplotlib.pyplot as plt
import mygrad as mg
import numpy as np
%matplotlib notebook

step1. 모델 클래스 정의하기;순전파

순전파란?

• 입력층에서 은닉층 방향으로 이동하면서 각 입력에 해당하는 가중치가 곱해지고, 결과적으로 가중치 합으로 계산되어 은닉층 뉴런의 함수 값(일반적으로 시그모이드(Sigmoid) 사용)이 입력된다. 그리고 최종 결과가 출력된다.

Batch란?

• 입력 data를 M개씩 묶어 batch를 이루는 개별적인 data에 대해 독립적으로 순전파 진행
• batch내 개별 데이터에 대한 함수값 F({vi},{wi},{bi}; xj)에 대한 연산은 독립적인 연산이며, 각 예측은 모델 파라미터, 데이터 값에만 의존
• M개를 shape-(M,1)의 numpy배열로 구성하여 순전파를 한번에 진행 할 수 있다.

근사함수 수식 정의

1. M개의 입력data xj에 대한 행렬곱 진행 -> xjXwi이 담긴 shape-(M,N)
2. 스칼라 bi가 shape-(M,N)인 행렬의 i번째 열에 각각 더해지도록 구현 -> bi를 shape-(1,N)인 행렬로 정의 xjXwi+bi
3. 행렬의 각 원소에 대한 시그모이드 함수값을 구해야 한다. -> sigmoid(xjXwi+bi)
4. 각 행별로 i번째 원소에 vi를 곱한 후 다 더해준다. -> vi를 shape(N,1)인 행렬로 정의 vi(sigmoid(xjXwi+bi))

모델 클래스 정의

• 1. 초기화(initialize): self.w, self.b, self.v를 표준 정규분포를 따르는 텐서 값으로 초기화한다.
• 2. init() 매서드 : 클래스 생성시 실행되며, 뉴런 N개를 받아 파라미터 초기화하는 역할
• 3. call(self, x) 매서드 : 입력데이터에 따른 순전파 수행, 모델을 이용해 x에 대한 예측값 계산, shape(M,1)의 예측값을 담은 텐서를 반환한다.
• 4. 매개변수 갱신 : 튜플 형태로 self.w, self.b, self.v return, 외부에서 주어진 매개변수로 모델의 매개변수 갱신

step2. 손실함수 작성

• universial approximation theorem에 의해 E>0에 대해 |F(x)-f(x)| < E를 만족시키는 모델파라미터 값이 무조건 존재한다.
• 손실함수 L(x) = |F(x)-f(x)| 가 0에 가깝게 되도록 학습시킨다. -> return값 batch size가 M인 batch의 예측값(prediction)에 대한 평균 손실

step3. 경사하강법 작성;역전파

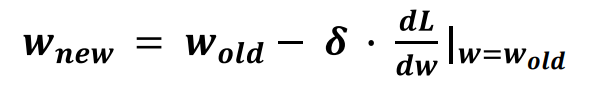
step4. 학습 : 순전파와 역전파 반복

• 학습용 데이터셋은 (xn, yn(true))쌍으로 구성
• train data와 truth를 잘 정의해야 한다.
• step1에서 정의한 Model class의 객체model을 생성하여 model parameters들이 초기화되도록 해야함
• 하이퍼파라미터인 batch size, 학습률, epoch수 등을 지정해준 상태에서 학습 시작
• 학습이후 근사모델 함수 F와 함수 f의 근사도 확인

step5. 학습과정 및 결과 확인

• 1.학습 진행에 따른 손실의 변화를 실시간 관찰
• 2. 각 뉴런별 학습 결과 그래프로 나타내기