신경망(Neural Network(NN))의 정의
- 입력 데이터와 출력 데이터 사이의 관계를 하나의 함수 관계로 연결해 표현해주는 인공지능 모델
- 모델 : 관찰한 데이터로부터 예측과 결정을 얻어내는 수학적 함수
신경망의 구조
- 입력 데이터와 출력 데이터 사이의 관계를 하나의 함수 관계로 연결을 표현해주는 인공지능 모델
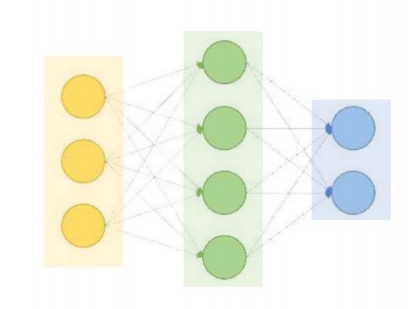
계층(layer)
- 같은 선상에 있는 노드들의 집합(입력층, 은닉층, 출력층)
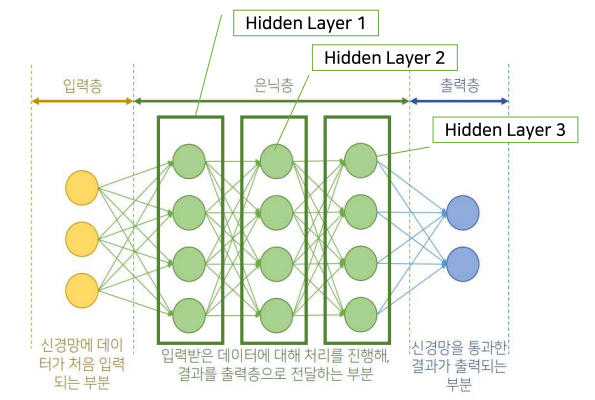
심층 신경망
- 은닉층의 개수가 2개 이상인 신경망
딥러닝(Deep Learning, DL)
- 심층 신경망에 대한 머신러닝
신경망의 흐름; 순전파(Feed-Forward NN)
- 순전파 : 데이터가 입력층, 은닉층, 출력층을 차례로 통과해 출력값이 나오는 과정
- 모든 뉴런이 공유하는 동일한 규칙
1) 각 뉴런에 입력되는 값은 여러개 가능, 그러나 출력되는 값은 오직 하나
2) 각 뉴런에 입력되는 값에 가중치가 곱해짐 - 은닉층
가중치 : wij(k) k번째 층의 i번째 뉴런과 k+1번째 층의 j번째 뉴런과 연결(최적의 가중치 찾는과정)
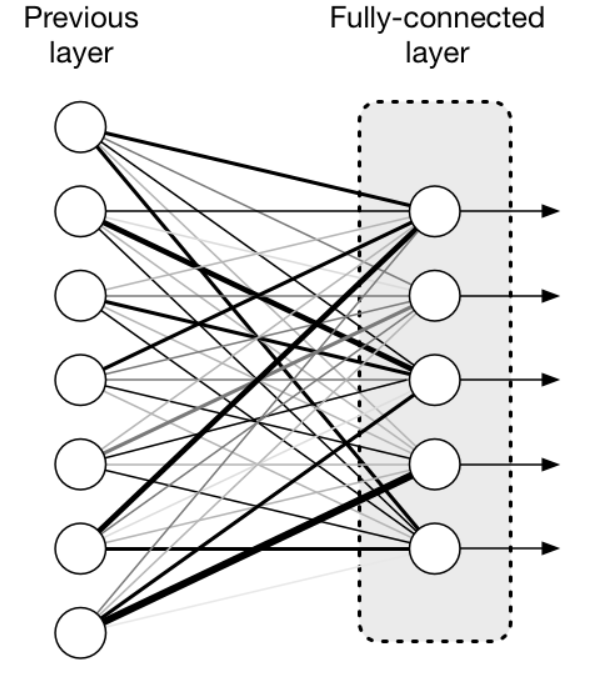
완전연결 계층(Fully-Connected Layer)
- 밀집층(dense later) or 완전연결 계층(fully-connected layer)
- 모든 입력 데이터에 대해 가중치를 곱하는 뉴런들로 이루어진 계층
- 각 층의 노드들끼리 완전하게 연결된 신경망의 layer
선형 신경망 vs 비선형 신경망
- 앞서 다룬 y = f(WT + b) 는 n차원에서 m차원으로서의 선형 변환
- 하지만 이는 현실 세계 데이터에서는 nonlinear dicision boundary를 가지는 데이터가 더 많음으로 중요한 요소를 놓칠 수도 있다.
- 각각의 출력되는 값이 활성화 함수를 통과하는 비선형 뉴런(Non linear nn)
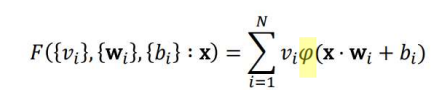
- 입력값(x)에 적절한 상수와 벡터 그리고 비선형 함수를 이용해 연산을 진행시키면 어떠한 수학적 함수 F로도 근사시킬 수 있다.
활성화 함수
- 뉴런에서 최종 값을 내보내기 전에 통과시켜주는 비선형 함수
활성화 함수 종류
- 함등함수
- σ(x) = x
- 주로 출력층에서 사용
- 회귀문제에서 많이 사용
2.sigmoid
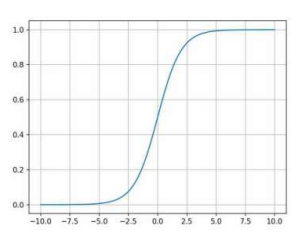
- σ(x) = 1/(1+e^(-x))
- 분류 문제에 많이 사용
- 출력값이 0~1 사이값이므로 해당 class에 속할 확률로 해석 가능
- DL 에서는 잘 사용하지 않음(이유: gradiant vanishing)
*gradiant vanishing : 역전파 과정에서 출력층에서 멀어질 수록 기울기 값이 매우 작아지는 현상 - 활성화 함수와 관련이 있다.
- sigmoid 함수의 미분함수는 |x|가 커질수록 0에 수렴한다. -> 역전파가 진행될수록 기울기 값이 0으로 수렴하게 되고 가중치 갱신이 일어나지 않는 문제가 발생한다.
- RELU
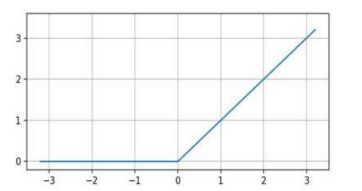
- σ(x) = max(x,0)
- gradiant vanishing 문제를 해결할 수 있다.
- 여전히 문제가 있으므로 Leaky RELU 이용
- softmax
- 입력값이 x1, x2, ..., xn, 출력값이 y1, y2,...yn일때
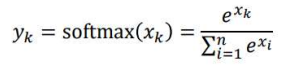
- 0<σ(xk)<1 이고 σ(xk) 값을 모두 더한 값은 1이다.
- 증가함수
- 각 class에 속할 확률로 해석가능 -> 다중분류 문제에 많이 사용된다.
활성화 함수를 이용하는 이유
1) 활성화 함수를 사용하지 않으면 선형모델만 표현가능
- 가중치를 곱해주는 과정은 선형 결합
- 비선형 함수를 추가해 보다 일반적인 수학적 표현 가능
- 정교한 규칙 모델링 가능
2) 활성화 함수를 이용해야 신경망의 층수를 증가시키는 것이 의미 있음
- 선형결합을 추가해봐야 한층을 사용하는거랑 똑같다.
- 비선형성이 추가됨
신경망의 학습
step1) 데이터 전처리
- 데이터셋을 잘 가공하는 것 -> NN이 더 효과적인 결과 보여줌
- data(feature) scaling : 데이터의 단위 값, 비율을 맞추는 것
- data binarizing: 데이터의 특성을 binary numbers로 바꾸는 것 -> 효율적인 알고리즘들을 분류하기 위해서
- data augmentation : 추가적인 데이터의 수집없이 training model에 사용할 데이터의 다양성을 증가시키기 위해(flip, crop,...)
step2) 신경망 모델 구성
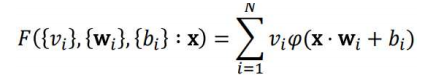
- 신경망이 F(x) 값에 가까운 값을 도출하도록 학습하는 것이 목적
- Layer수, layer종류, activation function 종류 결정하는게 중요
step3) 손실함수 정의 및 계산
- 실제값과 실험값의 오차로 모델의 성능 판단
1) SSE(오차 제곱합)
2) MSE(평균제곱오차)
3) |Residuals|(오차 절대값의 합)
4) cross entropy loss (교차 엔트로피 loss)
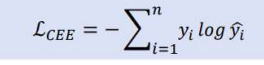
- 정보이론에서의 entropy란 사건의 확률을 사용하여 나타내는 사건에 있는 정보의 양
- 주로 회귀문제에서는 MSE 사용
- 분류문제에서는 CEE사용
step4) 손실함수 최적화(학습; back propagation)
- 손실함수 최적화 방법? optimizer
*optimizer - 경사하강법(GD)를 기반으로 손실함수를 최소화 하는 모델 파라미터를 찾는 알고리즘
- 기존 GD 단점 보완(local min 등)
- Adam, SGD...
- 편미분 계수 계산 : 오차 역전파법(back propagation)
- chain rule을 이용해 Loss의 gradiant 구한다.
신경망 모델의 표현-계산 그래프
계산 그래프
- 계산과정을 그래프로 표현
- 노드와 화살표로 표현
- 장점: 복잡한 계산을 쉽게 표현, 미분을 통한 역전파 계산이 효율적이고 쉬움
계산 그래프의 역전파
- 우리 목표는 각 변수에 대란 손실함수값의 미분을 구하는 것
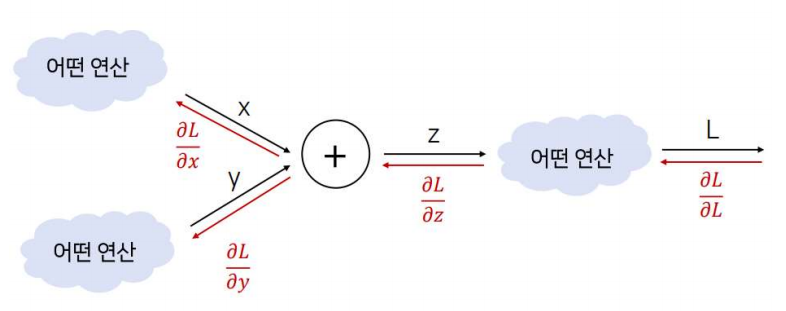
- 각 미분값을 구하는 것보다 앞의 계산 결과 활용
- 연쇄법칙 이용
affine layer
- 행렬곱을 이용해 순전파를 진행하는 계층
- 완전연결계층의 다른 이름, 즉 y = f(Wx+b) 진행
1 iteration의 정의
- 데이터 집합에 대한 순전파/ 역전파를 통해 가중치 업데이트 1회가 일어나는 것
- 실제로 N개의 전체 데이터를 M개씩 묶어 신경망에 입력하는데
- Batch: 한 번에 신경망에 입력하는 데이터 묶음
- Batch size: 1개의 batch내의 데이터의 수(=M)
- N개의 data를 랜덤하게 섞고 M개씩 골라 batch 생성
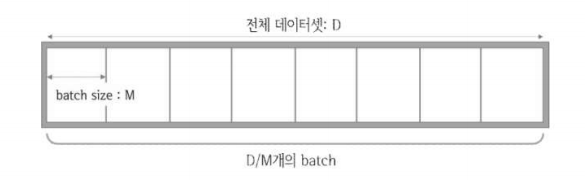
- 순전파 : 각 batch를 이루는 데이터에 대해 독립적으로 진행
- 역전파 : M개의의 데이터에서 계산된 손실함수의 평균을 이용해 진행
1epoch의 정의
- 전체 데이터에 대해 순전파 역전파를 통해 가중치 업데이트 1회가 일어나는 것
batch를 사용하는 이유
- 1개씩 학습 vs N개씩 묶어서 학습
1) 최적의 가중치를 향해 연속적이고 부드럽게 이동 - 개별 데이터는 서로 차이가 많이 나기 때문에 평균을 내서 가중치 업데이트
2) N개씩 묶어서 학습하는 것이 빠르고 효율적 - GPU의 병렬 연산을 활용 가능
- 효율적인 행렬곱 연산
3) 메모리 공간의 절약 + 학습 속도 향상 - 데이터 전체를 신경망에 입력하면 메모리 공간이 많이 소요됨
- 학습속도 저하
Hyperparameter
- 딥러닝 모델의 성능에 영향을 주는는 변수
- 사용자가 직접 설정해 학습과정에서는 변하지 않음
- parameter(가중치)를 효과적으로 업데이트 해 주기 위한 요소
