1. 경사하강법(Gradient Descent, GD)
- 함수값이 낮아지는 방향으로 독립 변수값을 이동하며 최솟값을 갖도록 하는 독립변수 값을 찾는 방법
경사하강법을 사용하는 이유
- Q)그냥 미분값 = 0 찾으면 되는거 아니냐?
- A) 미분이 힘들수도 있고 경사하강법이 미분보다 쉬운 경우 사용한다.
손실 함수
최적화(optimization)
- 딥러닝 최적화란 손실함수 값을 최소화 하는 모델 파라미터를 구하는 것
손실함수와 경사하강법
- 손실함수(L)가 w에 대한 일변수함수임을 가정하고 보여주겠다.
- 밑의 그림에서 볼 수 있듯이 손실함수를 따라 내려가며 극소값을 만족시키는 w를 찾는 과정을 경사 하강법이라 한다.

손실함수 표기
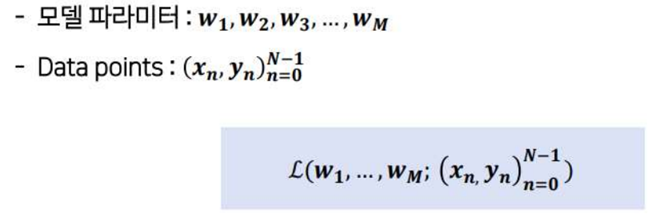
일변수 함수에서의 경사하강법
- L(w)의 최솟값을 찾아야 한다.
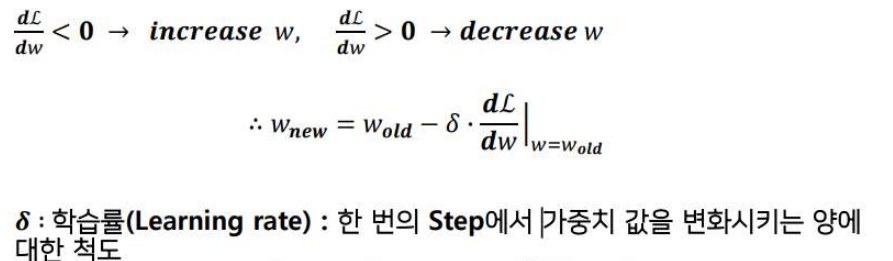
다변수 함수에서의 경사하강법
- 일변수 함수에서의 과정과 거의 동일하다.
- 차이점은 loss 함수의 미분값에서 모든 모델 파라미터에 대한 편미분을 진행한다.
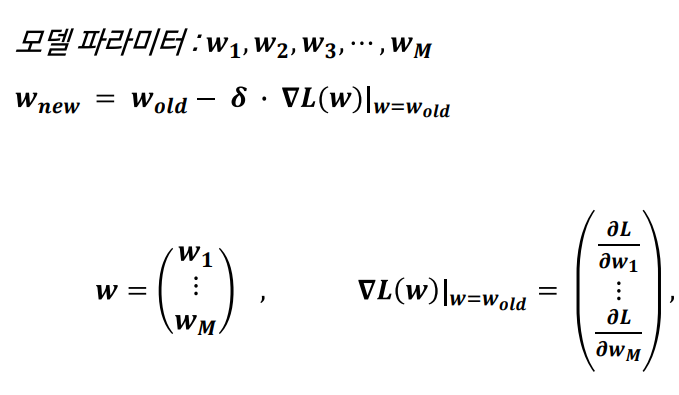
경사하강법에서의 hyperparameter
- 경사하강법 함수 내에서 사용되는 변수와 방법
-> 모델 파라미터 wold, learning rate, 경사하강 종료 시점, 반복 횟수
- wold : gaussian random distribute로 랜덤하게 선택된다.
- 학습률 : 10의 거듭제곱들을 학습률로 사용하여 진행
- criteria for stopping step(경사하강 종료 시점)
1) 사용자 판단
2) n번 반복후 변화 x시 종료
3) Thresholding : 특정값 이하로 gradiant 감소시 종료 - 반복 횟수
경사하강법의 한계
1.Local minimum
- 최저점이 아니라 극소점에서 최솟값으로 판단 할 수 있다.
- plateau
- 평탄 지역에서 학습 속도가 매우 느리며 느려지다 정지할 수 있다.
- data양이 많아지면 계산량이 증가한다.
