통계적 가설검정

모집단에 대해 어떤 가설을 설정하고, 그 모집단으로부터 추출된 표본을 분석함으로써,
그 가설이 틀리는지 맞는지 타당성 여부를 결정하는 통계적 기법이다.

Statistical Hypothesis Test

• 검정통계량 (Test Statistics)
• 가설 검정 (Hypothesis Test)
• 귀무 가설 H₀ (Null Hypothesis)
• 대립 가설 H₁ (Alternative Hypothesis)
• 유의수준 α (Significance Level)
• 기각역 (Critical Region, Rejection Region)
  • 임계치 (Critical Value)
  • 검정통계량이 기각역에 속하면, 귀무가설을 기각
• p-value (유의확률)
  • p-value < α : 귀무가설 기각
  • p-value > α : 귀무가설 채택

모평균에 대한 검정

모집단이 정규분포를 따르며, 모분산 σ₀² 이 알려진 경우

• Z ~ N(μ₀,σ₀²)
• σ₀²
• scipy.stats.norm 인스턴스 활용

가설의 종류	기각역에 의한 검정	p-value에 의한 검정
H₀: μ = μ₀ H₁: μ > μ₀	if Z > Zα, H₀ rejected if Z > stats.norm.isf(α), H₀ rejected	p_value ≤ α, H₀ rejected
H₀: μ = μ₀ H₁: μ < μ₀	if Z < -Zα, H₀ rejected if Z < stats.norm.ppf(α), H₀ rejected	p_value ≤ α, H₀ rejected
H₀: μ = μ₀ H₁: μ ≠ μ₀	if |Z| > Zα/2, H₀ rejected if |Z| > stats.norm.isf(α/2), H₀ rejected	p_value ≤ α, H₀ rejected

모집단이 정규분포를 따르며, 모분산 σ² 이 알려지지 않은 경우

• Z ~ N(μ₀,σ²)
• T ~ t(n-1)
• ddof = n - 1
• scipy.stats.t 인스턴스 활용

가설의 종류	기각역에 의한 검정	p-value에 의한 검정
H₀: μ = μ₀ H₁: μ > μ₀	if T > tα,n-1, H₀ rejected if Z > stats.t.isf(α, ddof), H₀ rejected	p_value = stats.t.sf(T) p_value ≤ α, H₀ rejected
H₀: μ = μ₀ H₁: μ < μ₀	if T < -tα, H₀ rejected if T < stats.t.ppf(α, ddof), H₀ rejected	p_value = stats.t.cdf(T) p_value ≤ α, H₀ rejected
H₀: μ = μ₀ H₁: μ ≠ μ₀	if |T| > tα/2, H₀ rejected if |T| > stats.t.isf(α/2, ddof), H₀ rejected	p_value = 2 * min(stats.t.sf(T), stats.t.cdf(T)) p_value ≤ α, H₀ rejected

scipy.stats.ttest_1samp 함수

• scipy.stats.ttest_1samp(sample, popmean) 함수 활용

  scipy.stats.ttest_1samp(
      a,
      popmean,
      axis=0,
      nan_policy='propagate',
      alternative='two-sided',
      *,
      keepdims=False,
  )

import numpy as np
import scipy.stats

sample = np.random.randn(100)
result = stats.ttest_1samp(sample, popmean=100)

print(result)
print(result.statistic)
print(result.pvalue)
print(result.df)

# 출력 결과
TtestResult(statistic=-901.7986066635818, pvalue=1.3444062839189925e-195, df=99)
-901.7986066635818
1.3444062839189925e-195
99

두 독립 모집단의 모평균 차이에 대한 검정

• `scipy.stats.ttest_ind(sample1, sample2, equal_var=True)`

scipy.stats.ttest_ind(
    a,
    b,
    axis=0,
    equal_var=True,
    nan_policy='propagate',
    permutations=None,
    random_state=None,
    alternative='two-sided',
    trim=0,
    *,
    keepdims=False,
) -> TtestResult

두 모집단이 정규분포이고, 모분산이 알려지지 않았지만 동일한 경우

• `scipy.stats.ttest_ind(sample1, sample2)` 함수 활용

import numpy as np
import scipy.stats

sample1 = np.random.randn(100) * 1.5
sample2 = np.random.randn(100) * 1.5
stats.ttest_ind(sample1, sample2)

print(result)
print(result.statistic)
print(result.pvalue)
print(result.df)

# 출력 결과
TtestResult(statistic=0.7944197743329069, pvalue=0.42790223519011494, df=198.0)
0.7944197743329069
0.42790223519011494
198.0

두 모집단이 정규분포이고, 모분산이 알려지지 않은 경우

• `scipy.stats.ttest_ind(sample1, sample2, equal_var=False)` 함수 활용

import numpy as np
import scipy.stats

sample1 = np.random.randn(100) * 1.5
sample2 = np.random.randn(100) * 1.7
result = stats.ttest_ind(sample1, sample2, equal_var=False)

print(result)
print(result.statistic)
print(result.pvalue)
print(result.df)

# 출력결과
TtestResult(statistic=-1.8363686911167, pvalue=0.06780564376279984, df=197.59327523235055)
-1.8363686911167
0.06780564376279984
197.59327523235055

대응표본(Paired Sample)에 대한 모평균 차이에 대한 검정

• `scipy.stats.ttest_rel(sample1, sample2)` 함수

scipy.stats.ttest_rel(
    a,
    b,
    axis=0,
    nan_policy='propagate',
    alternative='two-sided',
    *,
    keepdims=False,
) -> TtestResult

import numpy as np
import scipy.stats

sample1 = np.random.randn(100) * 1.5
sample2 = np.random.randn(100) * 1.7

result = stats.ttest_rel(sample1, sample2)

print(result)
print(result.statistic)
print(result.pvalue)
print(result.df)

# 출력 결과
TtestResult(statistic=-0.3963575170035945, pvalue=0.6926943211639452, df=99)
-0.3963575170035945
0.6926943211639452
99

두 독립 모집단의 중앙값(Median) 차이에 대한 검정

• Mann-Whitney U 검정 활용
• scipy.stats.mannwhitneyu(sample1, sample2) 함수 활용

import numpy as np
import scipy.stats as stats

sample1 = [23, 25, 28, 30, 32]
sample2 = [19, 21, 24, 26, 29]

alpha = 0.05

# Mann-Whitney U 검정
statistic, p_value = stats.mannwhitneyu(sample1, sample2)

print(f"statistic = {statistic}")
print(f"p_value = {p_value}")

if p_value < alpha:
    print("null hypothesis rejected.")
else:
    print("null hypothesis accepted.")

모분산에 대한 검정

• Z ~ N(μ₀,σ₀²)
• (n-1)S²/σ² ~ χ²(n-1)
• ddof = n - 1
• scipy.stats.chi2 인스턴스 활용

가설의 종류	기각역에 의한 검정	p-value에 의한 검정
H₀: σ² = σ₀² H₁: σ² > σ₀²	if χ² > χ²α,n-1, H₀ rejected if χ² > stats.chi2.isf(α, ddof), H₀ rejected	p_value = stats.chi2.sf(χ²) p_value ≤ α, H₀ rejected
H₀: μ = μ₀ H₁: μ < μ₀	if χ² < χ²1-α,n-1, H₀ rejected if χ² < stats.chi2.ppf(α), H₀ rejected	p_value = stats.chi2.cdf(χ²) p_value ≤ α, H₀ rejected
H₀: μ = μ₀ H₁: μ ≠ μ₀	if χ² > χ²α,n-1 or χ² < χ²1-α,n-1, H₀ rejected if χ² > stats.chi2.isf(α, ddof) or χ² < stats.chi2.ppf(α), H₀ rejected	p_value = 2 * min(stats.chi2.sf(χ²), stats.chi2.cdf(χ²)) p_value ≤ α, H₀ rejected

분산분석 (ANOVA)

• 연속형 자료에 대해 2개 이상의 그룹 간의 평균차이를 검정한다.
• 집단간의 평균차이가 있는지 없는지 검정한다.
• 귀무가설
  • 집단 간의 평균차이가 없다.
• 대립가설
  • 집단 간의 평균차이가 있다.

1. scipy.stats.f_oneway 함수 활용

• `scipy.stats.f_oneway(*samples)`

scipy.stats.f_oneway(
    *samples, 
    axis=0, 
    nan_policy='propagate', 
    keepdims=False
) -> F_onewayResult

import numpy as np
from scipy import stats

# 예제 데이터 생성
group1 = np.random.normal(20, 5, 100)
group2 = np.random.normal(22, 5, 100)
group3 = np.random.normal(19, 5, 100)

df = pd.DataFrame({"group1": group1, "group2": group2, "group3": group3})

statistic, p_value = stats.f_oneway(df["group1"], df["group2"], df["group3"])

print(f"statistic = {statistic}")
print(f"p_value = {p_value}")

# 출력 결과
statistic = 10.674059823981155
p_value = 3.3368970343403504e-05

2. statsmodels.api.stats.anova_lm 함수 활용

• statsmodels.api.stats.anova_lm(model)
  • statsmodels.formula.api.ols

import numpy as np
from scipy import stats
import statsmodels.api as sm
import statsmodels.formula.api as smf

# 예제 데이터 생성
# group1 = np.random.normal(20, 5, 100)
# group2 = np.random.normal(22, 5, 100)
# group3 = np.random.normal(19, 5, 100)

df = pd.DataFrame({"value": np.concatenate([group1, group2, group3]), "group": np.repeat(["group1", "group2", "group3"], [len(group1), len(group2), len(group3)])})

# ANOVA 수행
ols = smf.ols('value ~ C(group)', df).fit()
anova_table = sm.stats.anova_lm(ols)

print(anova_table)  # DataFrame 리턴

# 출력 결과
             df       sum_sq     mean_sq         F    PR(>F)
C(group)    2.0   497.143511  248.571755  10.67406  0.000033
Residual  297.0  6916.376013   23.287461       NaN       NaN

범주형 변수 적합도, 독립성 검정

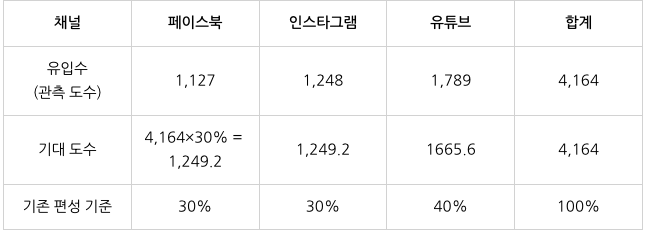
카이제곱 적합도 검정

하나의 범주형 변수에 대해 관측 값들이 기대하는 비율 분포를 따르는지 검정

scipy.stats.chisquare(
	f_obs, 
	f_exp=None, 
	ddof=0, 
	axis=0
) -> Power_divergenceResult

observed = np.array([1127, 1248, 1789])
expected = np.array([0.3, 0.3, 0.4]) * observed.sum()
dof=len(observed) - 1

statistic, p_value = stats.chisquare(observed, expected)

print(f"statistic = {statistic}")
print(f"p_value = {p_value}")

# 출력 결과
statistic = 21.09746237592058
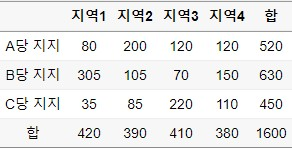
p_value = 2.6226736564792922e-05

카이제곱 독립성 검정

서로 다른 두 범주형 변수 간에 연관성이 있는지를 검정

stats.chi2_contingency(
	observed, 
	correction=True, 
	lambda_=None
) -> Chi2ContingencyResult

import pandas as pd
import scipy.stats as stats

df = pd.DataFrame({"지역1": [80, 305, 35], "지역2": [200, 105, 85], "지역3": [120, 70, 220], "지역4": [120, 150, 110]}, index=["A당 지지", "B당 지지", "C당 지지"])

result = stats.chi2_contingency(df)
# statistic, p_value, dof, expected_freq = stats.chi2_contingency(df)

print(f"statistic = {result.statistic}")
print(f"statistic = {result.pvalue}")
print(f"statistic = {result.dof}")
print(f"statistic = {result.expected_freq}")

# 출력 결과
statistic = 411.3522846166838
p_value = 1.0128548246241254e-85
dof = 6
expected_freq = [[136.5    126.75   133.25   123.5   ]
 [165.375  153.5625 161.4375 149.625 ]
 [118.125  109.6875 115.3125 106.875 ]]

pd.crosstab(index, columns)

pd.crosstab(
    index,
    columns,
    values=None,
    rownames=None,
    colnames=None,
    aggfunc=None,
    margins: 'bool' = False,
    margins_name: 'Hashable' = 'All',
    dropna: 'bool' = True,
    normalize: "bool | Literal[0, 1, 'all', 'index', 'columns']" = False,
) -> 'DataFrame'

• 코드 예시

import pandas as pd

# 예제 데이터
data = {
    'A': ['foo', 'foo', 'bar', 'bar', 'foo', 'bar'],
    'B': ['one', 'one', 'two', 'two', 'one', 'one'],
    'C': [1, 2, 3, 4, 5, 6]
}

df = pd.DataFrame(data)

# 기본 교차표
crosstab_basic = pd.crosstab(df['A'], df['B'])
print(crosstab_basic)

# 출력 결과
B    one  two
A            
bar    1    2
foo    3    0

# aggfunc 사용 (합계)
crosstab_sum = pd.crosstab(df['A'], df['B'], values=df['C'], aggfunc='sum')
print(crosstab_sum)

# 출력 결과
B    one  two
A            
bar  6.0  7.0
foo  8.0  NaN

# margins 사용 (합계 행과 열 추가)
crosstab_margins = pd.crosstab(df['A'], df['B'], margins=True)
print(crosstab_margins)
# 출력 결과
B    one  two  All
A                 
bar    1    2    3
foo    3    0    3
All    4    2    6

# dropna 사용 (NaN 제거)
df_with_nan = df.copy()
df_with_nan.loc[0, 'B'] = None
crosstab_dropna = pd.crosstab(df_with_nan['A'], df_with_nan['B'], dropna=True)
print(crosstab_dropna)

# 출력 결과
B    one  two
A            
bar    1    2
foo    2    0

# normalize 사용 (정규화)
crosstab_normalize = pd.crosstab(df['A'], df['B'], normalize='index')
print(crosstab_normalize)

# 출력 결과
B         one       two
A                      
bar  0.333333  0.666667
foo  1.000000  0.000000

상관분석 (Correlation Analysis)

• 두 변수 사이의 연관성에 관한 분석

피어슨 상관계수

Pearson Correlation Coefficient

• stats.pearsonr(x, y)
• 변수들이 연속형이고 정규 분포를 따를 때 주로 사용됩니다.

스피어만 상관계수

Spearman's Rank Correlation Coefficient

• stats.spearmanr(x, y)
• 변수들이 서열형(ordinal) 자료이거나, 연속형이지만 정규 분포를 따르지 않을 때 사용됩니다.

켄달 타우 상관계수

Kendall's Tau Correlation Coefficient

• stats.kendalltau(x, y)
• 순위 데이터를 비교할 때 사용됩니다.

코드 예시

import numpy as np
import pandas as pd
from scipy import stats

# 예제 데이터 생성
np.random.seed(0)
x = np.random.rand(100)
y = 2 * x + np.random.normal(0, 0.1, 100)

# 데이터프레임으로 변환
df = pd.DataFrame({'x': x, 'y': y})

# 피어슨 상관계수
corr, p_value = stats.pearsonr(df['x'], df['y'])
print(f"피어슨 상관계수: {pearson_corr}, p-값: {p_value}")

# 스피어만 상관계수
corr, p_value = stats.spearmanr(df['x'], df['y'])
print(f"스피어만 상관계수: {corr}, p-값: {p_value}")

# 켄달 타우 상관계수
corr, p_value = stats.kendalltau(df['x'], df['y'])
print(f"켄달 타우 상관계수: {corr}, p-값: {p_value}")

상관계수 행렬

# 피어슨 상관계수 행렬
pearson_corr_matrix = df.corr(method='pearson')
print("피어슨 상관계수 행렬:\n", pearson_corr_matrix)

# 스피어만 상관계수 행렬
spearman_corr_matrix = df.corr(method='spearman')
print("스피어만 상관계수 행렬:\n", spearman_corr_matrix)

# 켄달 타우 상관계수 행렬
kendall_corr_matrix = df.corr(method='kendall')
print("켄달 타우 상관계수 행렬:\n", kendall_corr_matrix)

정규성 검정 (Nomality Test)

• 데이터가 정규분포를 따르는지 검정

Shapiro-Wilk Normality Test

샤피로-월크 정규성 검정

• scipy.stats.shapiro(data)

Kolmogorov-Smirnov Test

콜모고로프-스미르노프 검정

• scipy.stats.kstest(data, "norm")
• ⚠️ data 파라미터에 StandardScaling 된 데이터를 넣어줘야 합니다.

D’Agostino-Pearson Test

다고스티노-피어슨 검정

• scipy.stats.normaltest(data)

```python
import scipy.stats as stats
from sklearn.preprocessing import StandardScaler

data1 = [117, 108, 105, 89, 101, 93, 96, 108, 108, 94, 93, 112, 92, 91, 100, 96, 120, 86, 96, 95]

stdScaler = StandardScaler()

std_data1 = stdScaler.fit_transform(pd.DataFrame(data1)).flatten()

statistic, p_value = stats.kstest(std_data1, "norm")
```

import scipy.stats as stats

import numpy as np

# data = stats.norm.rvs(size=100)
data = np.random.randn(100)

print(f"shpiro-wilk normality test = {stats.shapiro(data)}")
print(f"kolmogorov-Smirnov normality test = {stats.kstest(data, 'norm')}")
print(f"D'Agostino-Pearson normality test = {stats.normaltest(data)}")

# 출력 결과
shpiro-wilk normality test = ShapiroResult(statistic=0.9848038416985322, pvalue=0.3073893767936)
kolmogorov-Smirnov normality test = KstestResult(statistic=0.10383386500870145, pvalue=0.215652785442629, statistic_location=0.0346833095339652, statistic_sign=-1)
D'Agostino-Pearson normality test = NormaltestResult(statistic=1.364175080683408, pvalue=0.5055605120625232)