강의영상 링크는 다음을 클릭하시면 됩니다!
Lecture2와 3는 아직 작성 중에 있습니다. 곧 업로드할 예정이니 조금만 기달려주세요!

---

Introduction

지난 강의에서는 모델이 없을 때 policy를 evaluation하는 방법에 대해 배웠습니다. Model-Free 방법으로는 Monte Carlo(MC)와 Temporal Difference(TD)가 소개되었으며, DP와 이 두 개념을 비교함으로써 우리는 bias-variance와 bootstrapping에 있어서 명확한 차이를 알 수 있었습니다.

MDP(Markov Decision Process) 모델을 사용하면 게임, 로봇, 고객 광고 선택 등과 같은 다양한 분야에서 문제를 해결할 수 있습니다. 그러나 우리는 이러한 환경에 대해 모든 것을 알고 있지 않으므로, 샘플링된 방식을 통하여 접근하게 됩니다. 부분적으로 시행착오를 겪어가며 학습을 진행하지만, 이 환경은 현실적으로 많은 비용을 요구합니다. 이 문제는 Model Free Control을 통해 풀 수 있고, 이번 시간에 다룰 내용입니다.

1. Generalized Policy Iteration

Recall Policy Iteration

우리는 lecture 2에서 최적의 policy를 찾기 위한 Policy Iteration(PI)에 대해 배웠습니다. 기존의 PI는 임의의 policy를 initialize한 후, policy evaluation과 improvement를 반복했으며, 이때 policy evaluation은 $V^{\pi}$를 계산하고, policy improvement는 reward model과 dynamics model을 바탕으로 policy를 개선했습니다. 이 경우에는 우리에게 dynamics와 reward 모델이 주어졌기 때문에, 이전 policy와 비슷하거나 더 좋은 결과를 내게 됩니다. 따라서 우리는 더 개선된 policy나 이전과 같은 policy 중 선택하게 됩니다.

Model Free Policy Iteration

그렇다면 모델이 주어지지 않은 상황에서는 어떻게 달라질까요?

• Initialize policy $\pi$
• Repeat :
  • Policy evaluation : compute $Q^{\pi}$
  • Policy improvement : update $\pi$

Model Free PI도 기존의 PI와 전체적인 흐름은 같지만, policy evaluation에서 $V^{\pi}$가 아닌 $Q^{\pi}$를 계산한다는 점에서 차이를 보입니다. 여기서 Q-function은 state-action value function으로, $V$에 action 개념이 추가되었다고 생각하면 이해하기 쉽습니다. 따라서, 직접 계산한 Q-function의 value 값을 직접 사용하여 policy improvement 과정을 수행합니다. Q-function을 어떤 식으로 사용할 수 있는지에 관해서는 뒤에서 더 자세하게 설명될 것입니다.

MC for On Policy Q Evaluation

Q-function을 사용하는 방법 중 하나로 Monte Carlo가 소개되며, 알고리즘은 다음과 같습니다.

• Initialize $N(s,a) = 0$, $G(s,a) = 0$, $Q^{\pi}(s,a) = 0$, $\forall s \in S$, $\forall a \in A$

• Loop
  • Using policy $\pi$ sample episode $i = s_{i, 1}, a_{i,1}, r_{i,1}, ... s_{i, T_i}$
  • $G_{i,t} = r_{i,t} + \gamma r_{i,t+1} + \gamma^2r_{i, t+2} + ... + \gamma^{T_i-1}r_{i,T_i}$
  • For each state, action $(s,a)$ visited in episode $i$
    • For first or every time t that $(s,a)$ is visited in episode $i$
      • $N(s,a) = N(s,a) +1, G(s,a) = G(s,a) + G_{i,t}$
      • Update estimate $Q^{\pi}(s,a) = G(s,a)/N(s,a)$

위 알고리즘은 지난 강의의 “Monte Carlo policy evaluation”과 상당히 비슷해 보이지만, state value function이 아닌 state-action value function으로 수정하여 사용하고 있기 때문에, (state, action) 쌍으로 evaluation을 수행하게 됩니다.

Model-free Generalized Policy Improvement

Policy improvement는 evaluation에서 계산한 Q-function을 사용하여 policy를 개선해나갑니다. 그 과정은 생각보다 단순한데요, 우선 $Q(s,a)$를 비교하여 가장 가치가 높은 행동을 선택해, state에 대한 policy를 업데이트하는 것입니다.

이것은 Q-function으로 policy iteration을 하는 가장 기본적인 방법입니다. state에 대하여 특정 action을 취했을 때(→$Q(s,a)$), 가장 큰 Q 값을 갖는 best action을 사용할 수 있도록 하므로, model-free 방식에 해당합니다. 그러나, policy가 deterministic하다면, policy 안에 특정 action이 존재하지 않을 수도 있기 때문에, 우리는 더 이상 Q-function을 사용할 수 없게 됩니다. 따라서 우리는 Exploration이 필요하다는 결론을 내릴 수 있습니다.

2. Importance of Exploration

Policy Evaluation with Exploration

Generalized Policy Iteration(GPI)의 주된 목표는 ‘좋은’ policy $\pi$를 찾아나가면서, 최종적으로 최적의 policy에 수렴하는 것입니다. 따라서 우리는 ‘좋은’ $Q^{\pi}$ 추정치를 찾아야 최적 policy를 알 수 있게 됩니다.

이때, ‘좋은’ $Q^{\pi}$ 추정치는 어떻게 찾을까요? 모든 state에 따라 가능한 모든 action을 경험하면 됩니다. 그러나 model-free 환경에서 모든 (state, action) 쌍을 경험하기는 생각보다 어렵습니다. 환경이 어떻게 이루어져 있는지 알 수 없고, (state, action)에 대한 경우의 수도 다양하기 때문입니다. 이로 인해 우리는 좋은 추정치를 얻지 못할 수 있고, 학습 또한 제대로 이루어지지 않을 수도 있습니다. 이 문제에서 알 수 있듯이, 좋은 $Q(s,a)$를 구하기 위해서는 충분하고 지속적인 Exploration이 보장되어야 합니다.

$\epsilon$-greedy Policies

$**\epsilon$-greedy**는 exploration과 exploitation을 적절하게 섞은 방법으로, 0과 1 사이의 임의의 값을 갖는 $\epsilon$을 hyper-parameter로 사용합니다. 이때, $\epsilon$의 확률로 행동을 랜덤하게 선택하고, $1 - \epsilon$의 확률로 greedy한 행동을 선택합니다. $\epsilon$ 값에 따라서 exploration을 하거나 exploitation을 하는 단순한 알고리즘이지만, 지금까지도 유용하게 사용될 정도로 policy improvement가 잘 된다고 합니다.

Monotonic $\epsilon$-greedy Policy Improvement

이번에는 $\epsilon$-greedy 방식으로 Policy Improvement 했을 때, 잘 작동하는 지에 대해 수식으로 증명하는 과정입니다.

위 수식은 $V^{\pi_{i+1}}$이 $V^{\pi_i}$보다 항상 크거나 같음을 보이고 있으므로, $\epsilon$-greedy에 의하여 Policy Improvement가 정확히 작동하는 것을 알 수 있습니다.

Greedy in the Limit of Infinite Exploration(GLIE)

앞에서 배운 $\epsilon$-greedy 방법은 학습이 상당히 진행된 상황에서도 임의의 $\epsilon$ 값에 의하여 임의의 action을 하게 됩니다. $\epsilon$의 확률로 임의의 action을 한다면, 매 번 학습을 할 때마다 최적 policy 값이 달라질 수도 있습니다. 따라서 exploration을 조금 더 효율적으로 하기 위해 GLIE(Greedy in the Limit of Infinite Exploration)라는 새로운 알고리즘을 소개하고 있습니다.

GLIE는 다음 두 가지 조건을 만족해야 합니다.

• 모든 state-action pair(s,a)는 무한히 많은 횟수로 반복되어야 함.
  • $\lim\limits_{i\to∞}N_i(s,a) \to ∞$
• policy는 Q-function을 사용해 greedy한 action을 수행하는 policy로 수렴해야 함.
  • $\lim\limits_{i \to ∞}\pi(a|s) \to argmax_aQ(s,a)$ with probability 1

기존의 $\epsilon$-greedy에서는 $\epsilon$ 값을 임의로 설정하였다면, ****GLIE는 $1/i$로 설정하여, 학습이 진행될수록 $\epsilon$ 값을 점차 줄어들도록 만들었습니다. $i$가 무한대에 가까이 발산하게 된다면, $\epsilon$은 0으로 수렴하고 $(1 - \epsilon)$의 값은 1로 수렴하게 되므로, 항상 greedy한 action을 선택해 optimal policy에 도달하게 됩니다.

3. Monte Carlo Control

Monte Carlo Online Control / On Policy Improvement

Monte Carlo Control에 $\epsilon$-greedy와 GLIE를 적용한 알고리즘에 대해 살펴보겠습니다.

• Initialize $Q(s,a) = 0$, $N(s,a) = 0$, $\forall (s,a)$, Set $\epsilon = 1$, $k = 1$
  $\pi_k = \epsilon$-greedy(Q) // Create initial $\epsilon$-greedy policy
• loop
  • Sample $k$-th episode $(s_{k, 1}, a_{k,1}, r_{k,1}, .....s_{k,T})$ given $\pi_k$
    $G_{k,t} = r_{k,t} + \gamma r_{k,t+1} + \gamma^2r_{k,t+2}+ ... + \gamma^{T_i-1}r_{k,T_i}$
    for $t$ = 1, ..., $T$ do
    if First-visit to $(s,a)$ in episode $k$ then
    - $N(s,a) = N(s,a) + 1$
    - $Q(s_t, a_t) = Q(s_t, a_t) + \frac{1}{N(s,a)}(G_{k,t} - Q(s_t, a_t))$
    end if
    end for
    - $k = k + 1$, $\epsilon = 1/k$
    - $\pi_k = \epsilon$-greedy(Q) // Policy Improvement
• end loop

위에 있는 수도코드를 보면, Initialize 과정에서 policy를 $\epsilon$-greedy(Q)로 수정했음을 알 수 있습니다. 또한, for 문이 끝나고 k값을 1씩 더해준 후, 1에서 k만큼 나눠줌으로써 epsilon을 점차 줄여나가는 GLIE가 적용됨을 확인할 수 있습니다.

수도코드의 if문에서는 First-visit이라고 적혀 있지만, Every-visit도 가능하다고 합니다. Every-visit으로 MC Control을 수행한다면, First-visit에 비해 biased하지만 더 많은 데이터를 사용할 수 있다는 장점이 있습니다. 이 경우에는 (state, episode) 쌍의 counts를 유지하면서 Q-function을 업데이트해야 합니다. 해당 episode가 끝날 때마다, $k$와 $\epsilon$ 값을 업데이트 하고 Q에 관하여 새로운 $\epsilon$-greedy policy를 재정의합니다. 이렇게 하나의 episode가 끝나고, 그 다음 에피소드에도 같은 작업을 반복해주면 됩니다.

GLIE Monte-Carlo Control

• GLIE Monte-Carl control converges to the optimal state-action value function
  ⇒ $Q(s,a) \to Q^*(s,a)$

MC Control에 GLIE를 적용한다면, 결과적으로 state-action value function인 Q가 optimal로 수렴하게 됩니다. MC의 Evaluation 단계에서는 N과 Q 값을 update해주고, Improvement 단계에서는 $\epsilon$과 $\pi$( = $\epsilon$-greedy(Q))를 업데이트 합니다. 이때, optimal state-action value function은 $Q^*$로 표현합니다.

Model-free Policy Iteration

지난 시간에 배웠던 TD에 대하여 간단하게 복습해봅시다.

$V^{\pi}(s) = V^{\pi}(s) + \alpha( R + \gamma V^{\pi}(s^\prime) - V^{\pi}(s))$

TD는 MC와 마찬가지로 model-free한 방법 중 하나입니다. 위 수식, 즉 state value function $V^{\pi}(s)$는 보상의 합의 기댓값을 의미하고 있고, $R + \gamma V^{\pi}(s^\prime)$는 bootstrapping을 수행하여 기댓값을 샘플링합니다. TD Learning에는 bootstapping과 sampling을 수행해주는 부분이 존재하고, 이는 TD에 있어 핵심이라 할 수 있습니다. 반면, MC 방법은 sampling은 존재하지만 bootstrapping은 하지 않습니다. 또한, $(s, a, r, s^\prime)$을 지날 때마다 바로바로 업데이트하기 때문에, 굳이 episode가 끝날 때까지 기다리지 않아도 된다는 장점이 있었습니다.

이번 강의에서는 Model-free Control에 대해 다루고 있기 때문에, TD에서는 어떻게 사용할 수 있는지에 대해 알아보도록 하겠습니다.

4. Temporal Difference Methods for Control

Model-free Policy Iteration with TD Methods

Temporal Difference(TD) Control에 대해 알아봅시다. TD Control에서는 TD 기법과 $\epsilon$-greedy 방법을 사용하여 $Q^{\pi}$ 값을 계산하고, $\epsilon$-greedy($Q^{\pi}$)으로 policy improvement를 수행합니다. TD Control의 대표적인 예시로 SARSA와 Q-Learning이 있습니다. 먼저 SARSA에 대해 소개하도록 하겠습니다.

SARSA Algorithm: On-Policy

SARSA는 TD Control 중에서도 on-policy에 속하는 기법으로, (state, action, reward, state, action)을 사용하기 때문에 SARSA라는 이름이 붙여졌다고 합니다. on-policy learning은 직접 경험한 내용을 기반으로 policy를 예측하고 업데이트해 나가는 과정으로, 현재 action을 샘플링한 policy와 improvement하는 policy가 같습니다.

그렇다면, SARSA가 어떻게 policy improvement를 하는지 알아봅시다.

• Set initial $\epsilon$-greedy policy $\pi$, $t = 0$, initial state $s_t = s_0$
• Take $a_t$ ~ $\pi(s_t)$ // Sample action from policy
• Observe $(r_t, s_{t+1})$
• loop
  • Take action $a_{t+1}$ ~ $\pi(s_{t+1})$
  • Observe $(r_{t+1}, s_{t+2})$
  • $Q(s_t, a_t)$ ← $Q(s_t, a_t) + \alpha (r_t + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t))$
  • $\pi(s_t) = arg max_a Q(s_t, a)$ w.prob $1 - \epsilon$, else random
  • $t = t + 1$
• end loop

먼저, $\epsilon$-greedy policy를 임의로 initialize 해줍니다. 알고리즘은 MC Control 방법과 유사하지만, 다른 점은 Q-function을 업데이트하는 과정에서 사용된 $\alpha$라는 개념이 추가되었다는 점입니다. 또한, 첫 state $s_t$에서 $\epsilon$-greedy policy로 action $a_t$를 선택하고, 선택한 $a_t$를 실행하여 reward $r_t$와 $s_{t+1}$을 관측합니다. 그 이후에는 $s_{t+1}$에서 어떤 action $a_{t+1}$을 할지 선택하고 이러한 과정을 반복하면서 Q-function을 업데이트 합니다. SARSA의 장점으로는, TD 방식을 사용하기 때문에 모든 episode를 다 돌지 않아도 policy improvement가 가능하다는 점입니다. 따라서 episode가 긴 경우에 이 방법을 사용하면 효율적으로 최적 policy를 찾을 수 있을 겁니다.

SARSA도 Q-fuction이 optimal로 수렴하기 위해서는 다음 2가지의 조건을 만족해야 합니다.

1. policy sequence $\pi_t(a|s)$가 GLIE를 만족해야 함.
2. step size $\alpha_t$가 Robbins-Munro sequence를 만족해야 함.

   $\sum_{t=1}^{\infty}\alpha_t = \infty$
   $\sum_{t=1}^{\infty}\alpha^2_t \lt \infty$

GLIE 이외에도 step size에 대하여 조건이 붙는 이유는 step마다 업데이트가 일어나기 때문에 step size에 따라서 발산되는 경우도 있다고 합니다. 따라서 Q-function 값을 수렴하도록 하기 위해서는 $\alpha$ 값을 적절하게 사용해야 합니다. 그러나 실제 상황에서 $\alpha$ 값을 결정할 때 위 이론을 사용하지 않고 경험적으로 정한다고 합니다.

Q-Learning Algorithm: Off-policy

Q-Learning은 TD Control 기법 중에서도 off-policy에 해당됩니다. ****on-policy control은 샘플링한 policy와 학습으로 improvement하는 policy가 같다고 했습니다. off-policy는 on-policy와 반대로 두 대가 다른 것을 말합니다. Q-Learning에 대해 설명하면서 off-policy control도 함께 알아보겠습니다.

다음은 Q-Learning의 수도코드를 살펴봅시다.

• Initialize $Q(s,a)$, $\forall s \in S$, $a \in A$, $t = 0$, initial state $s_t = s_0$
• Set $\pi_b$ to be $\epsilon$-greedy w.r.t. Q
• loop
  • Take $a_t$ ~ $\pi_b(s_t)$ // Sample action from policy
  • Observe $(r_t, s_{t+1})$
  • $Q(s_t, a_t)$ ← $Q(s_t, a_t) + \alpha ((r_t + \gamma \max_{a^\prime} Q(s_{t+1}, a^\prime)) - Q(s_t, a_t))$
  • $\pi(s_t) = arg \max_a Q(s_t, a_t)$ w.prob $1 - \epsilon$, else random
  • $t = t + 1$
• end loop

Q-Learning은 먼저 Initialize 과정을 수행한 후, 바로 loop에 들어갑니다. initial state인 $s_t$에서 $\epsilon$-greedy로 $a_t$를 선택해서, $r_t$와 $s_{t+1}$을 받습니다. Q-function을 업데이트 하는 과정에서 Q-Learning은 SARSA와 달리, 현재 policy에서 샘플링하지 않고, 지금까지의 Q-function의 action 중 가장 큰 action으로 Q를 사용하여 policy improvement를 합니다. 여기서 $a^\prime$은 optimal policy에 포함되어 있는 action들로 생각하면 됩니다. 이때 Q-function을 초기화하는 것은 경험적으로 중요하며, 임의의 숫자나 0으로 초기화하는 것도 값이 수렴하는 데 도움이 될 수 있다고 합니다.

또한, $\epsilon$-greedy policy를 Q-learning에 적용할 때도, SARSA와 마찬가지로 GLIE를 만족해야 합니다. optimal policy로 수렴하기 위해서는 선택한 policy가 더욱 greedy 하도록 해야 합니다.

5. Maximization Bias

Maximization Bias

우리는 Q-Learning에서 Q-function을 계산하고 그 값에 대해 $\epsilon$-greedy를 수행하는데, bias가 maximize화하는 문제가 발생할 수 있다고 합니다. 그 이유는 max 연산을 하기 때문입니다. unbias 한 Q-function을 사용했더라도, 우리가 Q 값을 업데이트 하는 과정에서 max 연산을 하면 policy의 예측값은 bias 할 수 있습니다.

먼저, 단일 state의 MDP가 있다고 가정해봅시다. 이때 state는 1개이고 action은 2개가 존재합니다. action1과 action2의 random rewards의 평균은 모두 0이라고 할 때, $Q(s,a_1)$과 $Q(s,a_2)$, 그리고 $V(s)$도 0을 따르게 됩니다. 이 상황에서 Q로부터 유한한 샘플 추정치인 $\hat{Q}(s,a_1)$과 $\hat{Q}(s,a_2)$를 unbiased estimator로 계산을 해준 뒤 argmax 값을 $\hat{\pi}$에 할당합니다. 이제 왜 bias 해지는지 수식으로 증명하면 다음과 같습니다.

$\hat{V}^{\hat{\pi}} = E [ max(\hat{Q}(a_1), \hat{Q}(a_2))]$
$\ge max [ E(Q(a_1)), E(Q(a_2))]$ // 옌센 부등식
$= max[0,0]$
$= 0$
$= V^{\pi}$

따라서, Q-function이 bias하지 않더라도 연산을 하면서 bias하게 바뀔 수 있습니다.

Maximization Bias에 대해서는 마지막에 조금 더 자세하게 다루도록 하겠습니다.

Double Learning

Double Learning은 Maximization Bias 문제를 보완하기 위해 등장한 방법입니다. Q-function을 하나만 사용하지 않고, 서로 다른 Q-function 2개를 사용하여 독립적이면서 unbiased estimator를 생성합니다. Q-functions 중 하나는 어떤 action을 취할 지 결정하는데 사용하고, 다른 하나는 value 값을 계산하는데 사용됩니다. 이렇게 해줌으로써 estimator의 bias 문제를 해결할 수 있습니다.

Double Q-Learning

Double Q-Learning은 2개의 서로 다른 Q-function을 사용하는데, 50%의 확률로 첫 번째 Q-function을 업데이트하고, 또 다른 50%의 확률로 나머지 Q-function을 업데이트합니다.

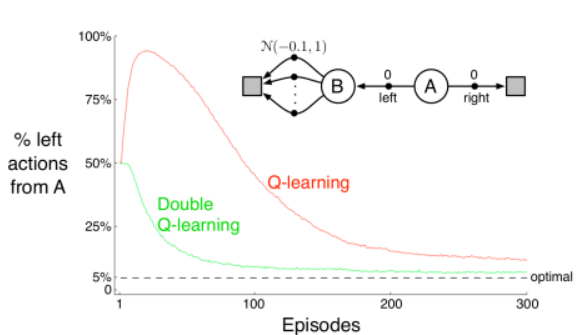
위 그림은 Q-Learning과 Double Q-Learning을 비교하는 그래프입니다. Task에 대해 먼저 설명해보면, 시작 state는 A입니다. A에서 오른쪽을 선택하면 바로 종료 지점으로 도착하지만, 이 경우에는 보상이 0입니다. 반대로, 왼쪽 방향으로 가면 state B로 이동하게 됩니다. B는 종료 지점이 아니고 이동에 따른 보상도 역시 0입니다. 그러나, 다음 상태에서의 다음 행동에 대한 보상이 평균은 -0.1, 표준편차는 1인 정규분포를 따르며 엄청나게 많은 action들로 구성되어 있습니다.

평균이 -0.1이기 때문에 좌측을 선택하는 것은 옳지 않을 수도 있지만, 우리의 알고리즘은 우측에 비해 좌측을 더 선호합니다. 그 이유는 오른쪽의 보상은 0으로 정해져 있지만, 왼쪽으로 갔을 때는 더 나은 보상을 얻을 수 있는 가능성이 있기 때문입니다. B state에서의 보상과 A state에서의 보상의 차이가 없더라도 더 나은 가능성에 의해 한쪽으로 치우치는 현상이 발생할 수 있으며, 이를 바로 Maximization Bias라고 합니다.

따라서, Q-Learning은 max 값을 Q-function에서 사용하기 때문에 결과적으로 위의 그래프와 같이 편향된 policy 예측값을 갖게 될 수 있고, Double Q-Learning은 편향된 정도가 Q-Learning에 비해 약해진 것을 볼 수 있으므로 이 문제를 개선해냈다고 볼 수 있습니다. 추가적으로, Double Q-Learning 기법이 더 빠른 속도로 수렴함을 알 수 있습니다.

Summary

이번 시간에는 Model-Free Control에 대해 배워보았습니다. 모델이 주어지지 않는 상황에서의 Policy Iteration에 대해 살펴보고, Model-free 방법에 맞게 V-function 대신에 state-action value function인 Q-function을 사용했습니다. 그러나, deterministic한 상황에서는 Q-function을 사용하지 못할 수 있기 때문에 exploration의 중요성을 강조합니다. 우리는 $\epsilon$-greedy라는 새로운 개념을 통하여 ‘좋은’ 추정치를 위한 충분한 exploration이 가능해졌습니다. 다만, 여기서 문제는 학습이 진행되더라도 우리는 $\epsilon$ 값을 임의로 설정하기 때문에, 매번 학습할 때마다 policy의 예측값이 수렴하지 않고 달라질 수 있다는 점입니다. 이를 개선하기 위해 GLIE(Greedy in the Limit of Infinite Exploration) 방법을 도입했습니다.

Model-Free 기법을 대표하는 3가지 알고리즘에 대해 배울 수 있었습니다. 첫 번째로는 Monte Carlo Control을 이야기했습니다. 우리가 기존에 알고 있던 MC에 GLIE와 \epsilon-greedy를 추가하여 optimal로 수렴하도록 하는 알고리즘이었습니다. 다음으로는 Temporal Difference Control 중에서 on-policy control에 해당되는 SARSA입니다. SARSA의 알고리즘은 MC와 유사하지만, \alpha라는 새로운 개념이 등장하고. optimal로 수렴하기 위해 GLIE와 적절한 \alpha값이 필요하다고 합니다. 마지막은 Temporal Difference Control에서도 off-policy에 속하는 기법인 Q-Learning입니다. Q-function에서 max 연산자를 사용하여 다음 state에 대하여 최적의 action을 선택한다는 점이 다른 두 Model-Free 기법과 구별되는 점입니다.

Q-Learning에서 max 연산자로 인해 unbiased 했던 Q-function을 사용했음에도 불구하고 policy의 예측값이 bias 할 수 있음을 강조했습니다. 이 문제를 Maximization Bias라고 정의합니다. 이를 보완하기 위해서 서로 다른 2 개의 Q-function을 사용하여, 하나는 action을 결정하고, 다른 하나는 value 값을 계산하는데 이용하게 됩니다. 이 방법을 Double Q-Learning이라 하며, 이로 인해 maximization bias(=over estimate)문제를 개선할 수 있었습니다.