병합정렬(MergeSort)의 완전 이해!

백준 기본문제: 24060번 병합정렬 알고리즘

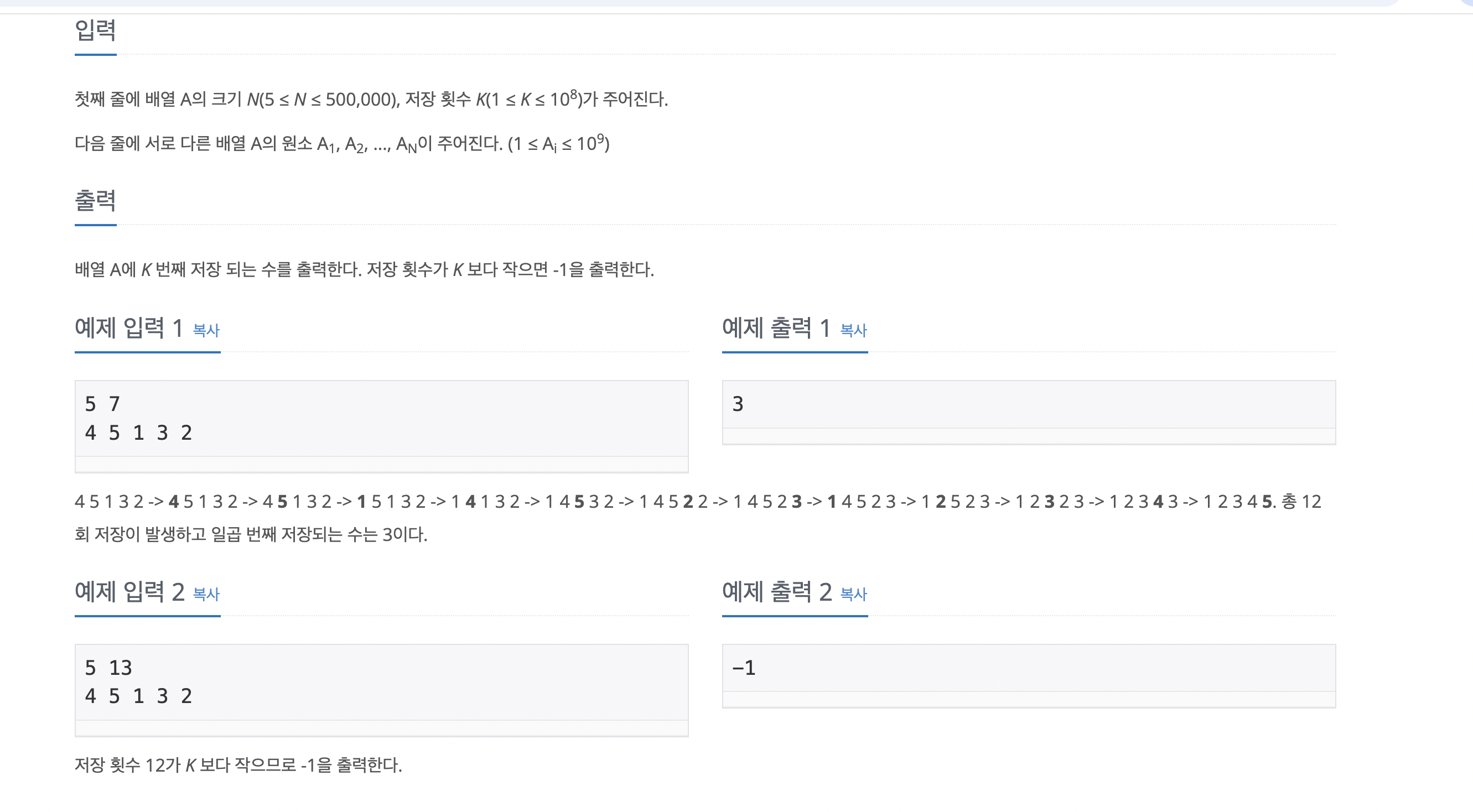
→ 병합 정렬을 이용한 문제,,, mergeSort() 함수 생성 그리고 재귀를 이용하여 N개의 배열에서 K번째로 정렬되는 숫자를 출력하게 하면 되는건가?

코드

package Baekjoon;

import java.io.*;
import java.util.*;

//병합 정렬로 배열 A를 오름차순 정렬할 경우 배열 A에 K 번째 저장되는 수를 구해라
public class beckjoon24060 {
    static int[] A; //입력배열
    static int[] temp; //병합 과정에서 임시로 사용될 배열
    static int count = 0; //저장 횟수 추정
    static int result = -1; //k번째 저장된 값을 저장
    public static void main(String[] args) throws IOException{
        BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
        String[] nums = br.readLine().split(" ");
        int N = Integer.parseInt(nums[0]);// 배열의 크기
        int K = Integer.parseInt(nums[1]); //병합 정렬의 저장 횟수
        //String 배열을 stream으로 변환 -> 스트림은 배열이나 컬렉션의 요소를 하나씩 처리할 수 있는 연속된 데이터의 흐름임.
        //.mapToInt-> 스트림의 각 요소를 변환하는 작업 수행
        A = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
        temp = new int[N];

        mergeSort(0,N-1,K);

        //K번째 값이 저장이 되지 않은 경우
        if(result == -1){
            System.out.println(-1);
        }else {
            System.out.println(result);
        }
    }
    public static void mergeSort(int left, int right, int K){
        if(left < right){
            int mid = (left + right) / 2;
            mergeSort(left, mid, K); // 왼쪽 절반 정렬
            mergeSort(mid + 1, right, K); // 오른쪽 절반 정렬
            merge(left, mid, right, K); // 병합
        }
    }
    public static void merge(int left,int mid, int right,int K){
        int i = left; //왼쪽 배열 시작
        int j = mid+1; //오른쪽 배열 시작
        int t = 0; //임시 배열 인덱스

        // 두 부분 배열 병합
        while (i <= mid && j <= right) {
            if (A[i] <= A[j]) {
                temp[t++] = A[i++];
            } else {
                temp[t++] = A[j++];
            }
        }

        //왼쪽 배열 남은 부분 자리
        while(i <= mid){
            temp[t++] = A[i++];
        }
        //오른쪽 배열 남은 부분 자리
        while(j <= right){
            temp[t++] = A[j++];
        }
        //임시 배열을 원본 배열로 복사
        for(int k=0; k<t; k++){
            A[left+k] = temp[k];
            count++; //저장 횟수 증가
            if(count ==K){
                result = A[left+k]; // K번째 저장된 값 저장
                return;// 더 이상 작업하지 않음
            }
        }
    }
}

→ 병합 정렬(Merge Sort)을 구현하여 배열을 오름차순으로 정렬하는 동안 K번째로 저장되는 값을 추적 하는 문제!

문제 요구사항

• 병합 정렬을 수행하면서 정렬된 값이 배열에 저장될때, 저장 순서대로 몇번째 값인지 추적해야합니다.
• K번째로 저장되는 값을 출력하되, K번째 저장작업보다 전체 배열의 병합정렬의 저장 작업이 작으면 -1을 출력하게 합니다.

static int[] A; //입력배열
static int[] temp; //병합 과정에서 임시로 사용될 배열
static int count = 0; //저장 횟수 추정
static int result = -1; //k번째 저장된 값을 저장

⚒️ 왜 static 전역변수를 썼을까?

• Static 키워드는 클래스 변수를 의미합니다.
• Static으로 선언된 변수는 클래스에 모든 메서드에서 공유되고, 인스턴스를 생성하지 않아도 접근이 가능합니다.
• 여기서, 병합정렬을 하는데 재귀함수(mergeSort) 사용하여 배열을 나누고 병합하는데, 이 과정에서 공유되는 데이터가 필요하기 때문입니다!

Main 함수

public static void main(String[] args) throws IOException {
    BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
    String[] nums = br.readLine().split(" ");
    int N = Integer.parseInt(nums[0]); // 배열의 크기
    int K = Integer.parseInt(nums[1]); // 병합 정렬의 저장 횟수

    A = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
    temp = new int[N];

    mergeSort(0, N - 1, K);

    // K번째 값이 저장되지 않은 경우
    if(result == -1) {
        System.out.println(-1);
    } else {
        System.out.println(result);
    }
}

• main 함수는 프로그램의 입력 처리와 병합 정렬 호출, 그리고 결과 출력까지 전반적인 흐름을 관리합니다.
• 특히,mergeSort(0 , N-1, K); 를 호출하여 배열 전체 구간의 [0,N-1]를 병합 정렬 합니다.

MergeSort 함수

public static void mergeSort(int left, int right, int K) {
    if (left < right) {
        int mid = (left + right) / 2;
        mergeSort(left, mid, K); // 왼쪽 절반 정렬
        mergeSort(mid + 1, right, K); // 오른쪽 절반 정렬
        merge(left, mid, right, K); // 병합
    }
}

• 분할(Divide)을 통해 재귀적으로 분할합니다!
• 병합(Merge)을 통해 분할된 배열을 정렬합니다!

int mid = (left + right) / 2;
mergeSort(left, mid, K); // 왼쪽 절반 정렬
mergeSort(mid + 1, right, K); // 오른쪽 절반 정렬
merge(left, mid, right, K); // 병합

• left와 right 기준으로 배열을 절반으로 나눕니다.
• mid = (left + right) / 2를 통해 중간지점을 찾습니다.
• 왼쪽 절반 [left, mid] 와 오른쪽 절반[mid+1, right] 로 나누어 mergeSort를 재귀적으로 호출합니다!
• merge(left, mid, right, K) 병합 과정에서 K번째 저장 작업을 추적하기 위해 전달되는 값입니다.

Merge 함수

public static void merge(int left, int mid, int right, int K) {
    int i = left; // 왼쪽 부분 배열의 시작 인덱스
    int j = mid + 1; // 오른쪽 부분 배열의 시작 인덱스
    int t = 0; // 임시 배열(temp) 인덱스

    // 두 부분 배열 병합
    while (i <= mid && j <= right) {
        if (A[i] <= A[j]) {
            temp[t++] = A[i++];
        } else {
            temp[t++] = A[j++];
        }
    }

    // 왼쪽 배열의 남은 값 처리
    while (i <= mid) {
        temp[t++] = A[i++];
    }

    // 오른쪽 배열의 남은 값 처리
    while (j <= right) {
        temp[t++] = A[j++];
    }

    // 병합된 결과를 원래 배열 A에 복사
    for (int k = 0; k < t; k++) {
        A[left + k] = temp[k];
        count++; // 저장 횟수 증가
        if (count == K) {
            result = A[left + k]; // K번째 저장된 값 저장
            return; // 더 이상 작업하지 않음
        }
    }
}

• 두 정렬된 부분을 하나의 정렬된 배열로 병합합니다.

while (i <= mid && j <= right) {
    if (A[i] <= A[j]) {
        temp[t++] = A[i++]; // 왼쪽 배열 값이 작거나 같으면 temp에 저장
    } else {
        temp[t++] = A[j++]; // 오른쪽 배열 값이 작으면 temp에 저장
    }
}

• 왼쪽 배열과 오른쪽 배열을 비교하여 작은 값을 임시배열인 temp에 저장합니다.
• 각각의 인덱스 ( i 또는 j)를 증가시킵니다.

왼쪽 배열의 남은 값

while (i <= mid) {
    temp[t++] = A[i++]; // 왼쪽 배열에 남은 값을 temp에 저장
}

오른쪽 배열에 남은 값

while (j <= right) {
    temp[t++] = A[j++]; // 오른쪽 배열에 남은 값을 temp에 저장
}

• 한쪽 배열이 모두 temp에 복사된 후, 다른 쪽 배열에 남아 있는 값들을 그대로 temp에 추가합니다.

병합 결과를 원본 배열에 복사

for (int k = 0; k < t; k++) {
    A[left + k] = temp[k];// 병합된 값을 원본 배열로 복사
    count++; // 저장 횟수 증가
    if (count == K) { //K번째 저장된 값 추척
        result = A[left + k]; // K번째 저장된 값 저장
        return; // 더 이상 작업하지 않음
    }
}

표로 풀어쓴 과정!

단계	병합 구간	결과 배열	저장 순서
분할	[4, 5, 1, 3, 2]	[4, 5, 1], [3, 2]
병합 1	[4], [5]	[4, 5]	4 → 5
병합 2	[4, 5], [1]	[1, 4, 5]	1 → 4 → 5
병합 3	[3], [2]	[2, 3]	2 → 3
병합 4	[1, 4, 5], [2, 3]	[1, 2, 3, 4, 5]	결과: 3

병합정렬(MergeSort)은 나누어질 수 없을때까지 분할을 하며 이후에 정렬을하며 병합을 합니다. 분할을 반복하는 과정에서 재귀(Recursion)함수가 필수적으로 쓰이며, 시간복잡도는 O(n)입니다. 이해가 쉽게 문제에 대한 코드를 쪼개서 풀이를 했으니 여러분들도 이번 기회에 병합정렬에 대한 정확한 동작을 이해하시고 넘어가셨으면 합니다!! 다음 포스팅에서 뵙겠습니다❣️