코딩테스트에서 정렬은 기본 중의 기본이지만, 실제로 심층적인 이해와 응용이 요구되는 경우도 많습니다. 정렬 알고리즘의 종류와 각각의 특징을 이해하고, 적합한 상황에서 이를 선택할 수 있는 능력을 기르는 것이 중요합니다. 여기서는 정렬의 개념, 종류, 특징, 그리고 정렬 알고리즘의 심화 주제까지 다루어볼게요.
📌 정렬의 개념
- 정렬은 데이터를 특정 기준에 따라 오름차순(Ascending) 또는 내림차순(Descending)으로 배열하는 작업입니다.
- 정렬은 대부분의 코딩테스트에서 문제 해결의 기본 도구로 사용되며, 다음과 같은 상황에서 자주 등장합니다:
- 데이터를 정리하여 탐색이나 검색을 빠르게 하기 위해
- 특정 조건에 따라 데이터를 조합하거나 그룹화하기 위해
- 순서를 기반으로 한 로직을 구현하기 위해
📌 정렬 알고리즘의 분류
- 정렬 알고리즘은 크게 비교 기반 정렬과 비비교 기반 정렬로 구분할 수 있습니다.
1. 비교기반 정렬
데이터 간의 비교를 통해 정렬을 수행하여, 일반적으로O(NlogN) 이상의 복잡도를 가집니다.
- 버블 정렬 (Bubble Sort)
- 삽입 정렬 (Insertion Sort)
- 선택 정렬 (Selection Sort)
- 퀵 정렬 (Quick Sort)
- 병합 정렬 (Merge Sort)
- 힙 정렬 (Heap Sort)
2. 비비교 기반 정렬
데이터를 비교하지 않고, 데이터의 특징(값의 범위 등)을 활용하여 정렬합니다.
대표적인 알고리즘:
- 계수 정렬 (Counting Sort)
- 기수 정렬 (Radix Sort)
- 버킷 정렬 (Bucket Sort)
📌 정렬 알고리즘의 종류와 특징
아래는 주요 정렬 알고리즘의 종류와 특징을 정리한 표입니다:
| 정렬 알고리즘 | 시간 복잡도 OOO | 공간 복잡도 | 안정 정렬 여부 | 특징 및 활용 |
|---|---|---|---|---|
| 버블 정렬 | O(N^2) | O(1) | ✅ | 기초적인 알고리즘, 구현 연습용 |
| 삽입 정렬 | O(N^2) | O(1) | ✅ | 데이터가 거의 정렬된 경우 효율적 |
| 선택 정렬 | O(N^2) | O(1) | ❌ | 작은 배열에서 간단하게 사용 가능 |
| 퀵 정렬 | 평균 O(NlogN) 최악 O(log^2) | O(logN) | ❌ | 빠르고 메모리 효율적, 대부분의 상황에서 유리 |
| 병합 정렬 | O(NlogN) | O(N) | ✅ | 안정적이고 대규모 데이터에 적합 |
| 힙 정렬 | O(NlogN)O(N \log N)O(NlogN) | O(1) | ❌ | 메모리 사용이 제한적인 환경에서 적합 |
| 계수 정렬 | O(N+K) | O(K) | ✅ | 데이터의 범위가 작을 때 매우 빠름 |
| 기수 정렬 | O(N⋅d) | O(N+K) | ✅ | 정수 또는 문자열 정렬에 적합 |
| 버킷 정렬 | 평균 O(N+K) | O(N) | ✅ | 실수 정렬이나 분포가 균등한 데이터에 적합 |
Java에서는 Arrays와 Collections 클래스의 메서드를 사용하여 효율적으로 정렬을 구현할 수 있습니다. 라이브러리를 활용하면 간단한 코드로 정렬을 처리할 수 있으면서도 다양한 상황에 맞는 정렬 알고리즘을 학습할 수 있습니다. 아래는 정렬 알고리즘의 종류와 Java 예시 코드를 소개합니다.
📌 정렬 알고리즘의 Java 예시 코드
1️⃣ 버블 정렬 (Bubble Sort)
📌 알고리즘 설명
- 인접한 두 원소를 비교하여, 필요하면 자리를 바꿉니다.
- 한 번의 반복(iteration)으로 가장 큰 값이 맨 뒤로 이동합니다.
- 전체 배열이 정렬될 때까지 반복합니다.
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {5, 3, 8, 4, 2};
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) { // 인접 원소 비교
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
// 결과 출력
for (int num : arr) {
System.out.print(num + " ");
}
}
}2️⃣ 삽입 정렬 (Insertion Sort)
📌 알고리즘 설명
- 두 번째 원소부터 시작하여, 해당 원소를 정렬된 부분 배열의 올바른 위치에 삽입합니다.
- 데이터가 이미 정렬된 경우 매우 효율적입니다.
public class InsertionSort {
public static void main(String[] args) {
int[] arr = {5, 3, 8, 4, 2};
for (int i = 1; i < arr.length; i++) {
int key = arr[i];
int j = i - 1;
// key 값보다 큰 값들을 오른쪽으로 이동
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
// 결과 출력
for (int num : arr) {
System.out.print(num + " ");
}
}
}3️⃣ 선택 정렬 (Selection Sort)
- 배열에서 가장 작은 원소를 찾아 첫 번째 자리로 이동합니다.
- 나머지 배열에 대해 이 과정을 반복합니다.
public class SelectionSort {
public static void main(String[] args) {
int[] arr = {5, 3, 8, 4, 2};
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {//i+1부터 끝까지 탐색
if (arr[j] < arr[minIndex]) {
minIndex = j; // 최소값 인덱스 갱신
}
}
// 최소값과 교환
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
// 결과 출력
for (int num : arr) {
System.out.print(num + " ");
}
}
}4️⃣ 퀵 정렬 (Quick Sort)
📌 알고리즘 설명
- 피벗(pivot)을 기준으로 데이터를 두 부분으로 나누고, 각 부분을 정렬합니다.
- 재귀적으로 동작하며, 대부분의 경우 효율적입니다.
- 평균적으로 O(NlogN)의 시간 복잡도를 가집니다.
- 퀵 정렬은 재귀적 구조를 사용하므로 “분할 정복” 패턴을 학습하는데 유용합니다.
- Java의
Arrays.sort()는 Dual-Pivot Quick Sort를 기본으로 사용합니다. 코딩테스트에서 효율적인 라이브러리를 사용할 때 퀵 정렬 기반 알고리즘이 동작할 가능성이 큽니다.
📌 퀵 정렬의 동작
public class QuickSort {
public static void main(String[] args) {
int[] arr = {5, 3, 8, 4, 2};
// 퀵 정렬 호출 (배열 전체를 정렬)
quickSort(arr, 0, arr.length - 1);
// 결과 출력
for (int num : arr) {
System.out.print(num + " ");
}
}
// 퀵 정렬 메서드 (재귀적으로 배열을 정렬)
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
// 배열을 피벗을 기준으로 두 부분으로 나누고, 피벗의 위치 반환
int pivotIndex = partition(arr, low, high);
// 피벗 왼쪽 부분 정렬 (재귀 호출)
quickSort(arr, low, pivotIndex - 1);
// 피벗 오른쪽 부분 정렬 (재귀 호출)
quickSort(arr, pivotIndex + 1, high);
}
}
// 배열의 구간을 피벗을 기준으로 나누는 메서드
public static int partition(int[] arr, int low, int high) {
// 피벗 선택 (구간의 마지막 원소를 피벗으로 설정)
int pivot = arr[high];
// i는 피벗보다 작은 값을 저장할 위치를 추적
int i = low - 1; //피벗보다 작은 값들을 저장할 마지막 위치를 가리키도록 한다.
// low부터 high-1까지 반복하며 피벗과 비교
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
i++;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// 피벗을 올바른 위치(i+1)로 이동
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}
}
5️⃣ 병합 정렬 (Merge Sort)
📌 알고리즘 설명
- 배열을 두 부분으로 나누고, 각각을 정렬한 후 병합합니다.
- 재귀적으로 동작하며, 항상 O(NlogN) 복잡도를 가집니다.
📌 병합정렬의 동작과정
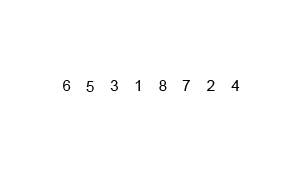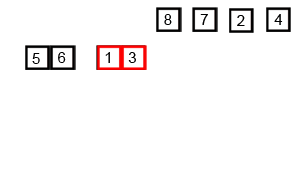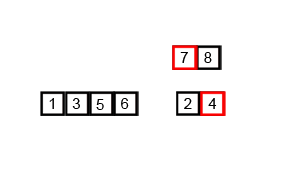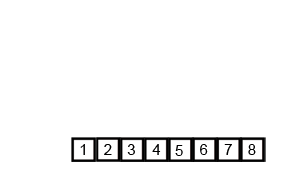
📌 병합정렬의 동작
public class MergeSort {
public static void main(String[] args) {
int[] arr = {5, 3, 8, 4, 2};
mergeSort(arr, 0, arr.length - 1);//mergeSort 함수를 호출하여 배열 전체를 정렬
// 결과 출력
for (int num : arr) {
System.out.print(num + " ");
}
}
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2; //중간 지점 계산
mergeSort(arr, left, mid); //왼쪽부분 정렬
mergeSort(arr, mid + 1, right); //오른쪽부분 정렬
merge(arr, left, mid, right); //정렬된 두 부분 정렬
}
}
//병합 함수
public static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1]; //임시 배열 생성
int i = left //왼쪽 구간 시작 인덱스
int j = mid + 1 //오른쪽 구간 시작 인덱스
int k = 0; //k: temp 배열 인덱스
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++]; //왼쪽값 선택
} else {
temp[k++] = arr[j++]; //오른쪽값 선택
}
}
//왼쪽구간에 남은 값 추가
while (i <= mid) temp[k++] = arr[i++];
//오른쪽구간에 남은 값 추가
while (j <= right) temp[k++] = arr[j++];
//병합된 결과를 원래 배열에 복사
for (int t = 0; t < temp.length; t++) {
arr[left + t] = temp[t];
}
}
}오늘은 정렬의 종류에 대해 공부해보았습니다! 다음 포스팅에서는 병합정렬 문제풀이를 하며 같이 공부해보도록 합시다!
