1. 플로이드-워셜(Floyd-Warshall) 알고리즘이란?
- 모든 최단 경로를 구하는 문제(All pairs shortest path problem).
다익스트라는 하나의 정점에서 다른 모든 정점까지의 최단 거리를 구하는 알고리즘(S.S.S.P - Single Source Shortest Path) 이었다면, 플로이드-워셜 알고리즘은 한 번 실행하여 모든 노드 간 최단 경로를 구할 수 있다
- 플로이드-워셜 알고리즘은 다익스트라 알고리즘과는 다르게 음의 간선도 사용할 수 있다.
2. 알고리즘의 작동 방식
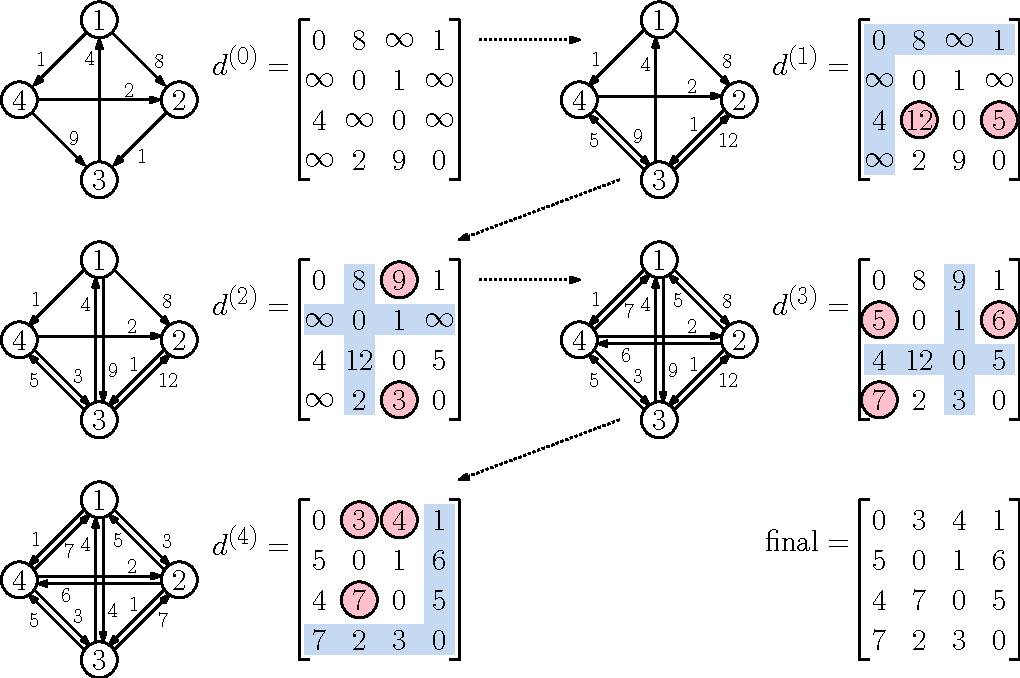
모든 노드 간의 최단거리를 구해야 하므로 2차원 인접 행렬을 구성한다.(노드i 부터의 노드 j까지의 비용 S = (graph[i][j] = S) 알고리즘은 여러 라운드로 구성된다. 라운드마다 각 경로에서 새로운 중간 노드로 사용할 수 있는 노드를 선택하고, 더 짧은 길이를 선택하여 줄이는 과정을 반복한다.
즉 i부터 j까지의 최소거리가 있을때 중간노드인 k가 들어왔을때 i 부터 k까지의 거리와 k부터 j까지의 거리 값이 더 작다면 값이 갱신된다.
3. 소스코드로 구현
플로이드-워셜 알고리즘은 시간 복잡도가 O(n^3)으로, 그래프의 크기가 작아 세제곱 시간 알고리즘을 적용해도 문제가 풀릴 때만 사용할 수 있다.
N = len(graph)
for mid in range(N):
for start in range(N):
for end in range(N):
if graph[start][end] > graph[start][mid] + graph[mid][end]:
graph[start][end] = graph[start][mid] + graph[mid][end]
4. 경로구하기
최단 경로 행렬 D 를 통해 i 번째 정점에서 j 번째 정점까지 최단경로를 구할 수 있었다. 정확히는 최단경로로 갈 때의 가중치를 구하는 것이기 때문에 어떤 정점을 거쳐 가는지는 알 수 없다.
따라서 이를 위해 직전 정점 행렬 pi라고 정의해보자. pi[i][j]에는 i부터 j까지가는 정점의 직전의 정점을 의미한다.
따라서 pi 행렬을 초기화 할때는 pi[i][j] = i가 된다. 또한 값이 갱신 되는 경우는 작은 값으로 교체될때마다 pi[i][j] = pi[k][j] 값이 된다. 따라서 경로를 구하기 위한 코드는 다음과 같다.
N = len(graph)
for mid in range(N):
for start in range(N):
for end in range(N):
if graph[start][end] > graph[start][mid] + graph[mid][end]:
graph[start][end] = graph[start][mid] + graph[mid][end]
pi[start][end] = pit[mid][end]
