Tarjan's Strongly Connected Component (SCC) Algorithm

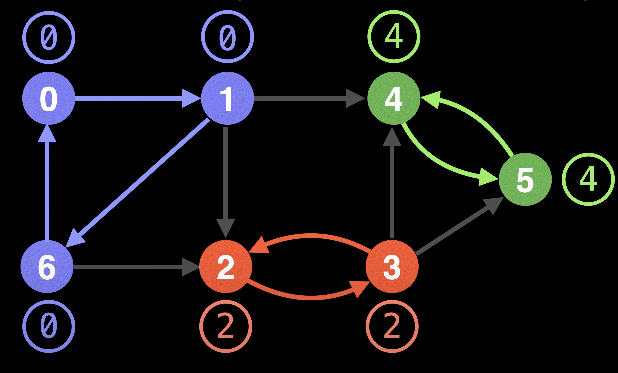
SCC는 무엇인가?

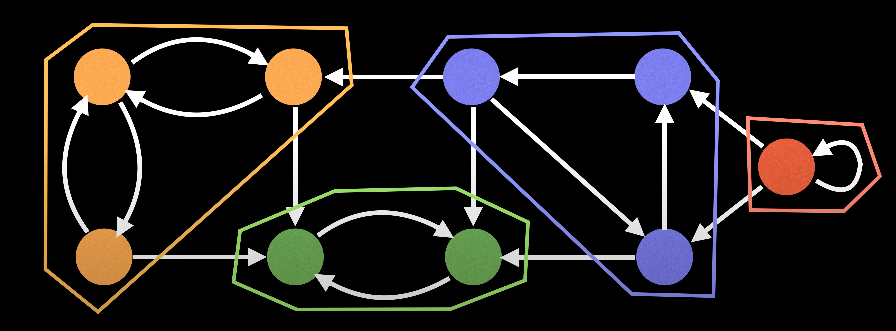
1. 같은 SCC 내의 임의의 두 정점 A,B사이의 경로가 항상 존재한다.

2. 서로 다른 SCC에서 뽑은 임의의 두 점 A,B 사이의 경로 A->B로 가는 경로와 B->A로 가는 경로는 동시에 존재할 수 없다. (SCC 끼리는 사이클이 존재하지 않는다.)

LOW-LINK Values

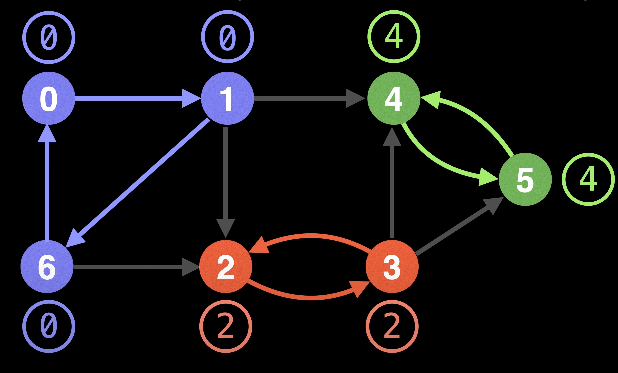
SCC를 찾기위해 사용되는 알고리즘으로 DFS를 통해 해당 노드가 방문 할 수있는 가장 작은수를 단순히 저장 하는것이다. 하지만 해당 방법은 노드의 시작위치,방문 순서등에 따라 달라지므로 완벽한 알고리즘이라고 할 수 없다.

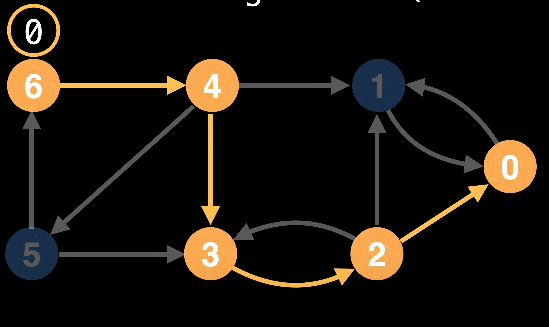
여기서 새로운 조건을 하나 추가하자면 그래프의 연결 돼있는 U노드와 V노드중 현재 우리가 있는 노드가 U노드이고 U - V 사이의 Love Values를 업데이트 하기 위해선 V가 스택에 존재해야한다.

1. 우선 모든 노드들을 방문하지 않은 상태로 둔다. DFS를 시작하고 방문하는 노드들에게 low-link value를 저장한다. 또한 현재 노드를 방문 처리하고 스택에 넣는다.

2. DFS 콜백을 하면서 만약 이전의 노드가 스택에 있다면 현재 노드의 low-link value와 이전 노드의 low-link value중 작은 값을 저장한다.

3. 갈 수 있는 모든 노드를 방문 한다음 만약 현재 노드가 Connected Component라면 현재 노드까지 모든노드를 스택에서 제거한다

UNVISITIED = -1
n = #그래프의 노드 갯수
graph = #인접 리스트로 구현한 그래프

id = 0 # 각각에 노드에게 id 부여
sccCount = 0 # SCC가 몇개인지 세기 위한 변수

ids = [-1] * n  # 각각의 id 저장
low = [0] * n # 각각의 low-link 저장
onStack = [False] * n # 스택에 있는지 확인
stack = []

def findSccs():
	for i in range(n):
    		if(ids[i] == UNVISITED):
        		dfs(i)
     	return low
        
        
def dfs(current):
	stack.append(current)
    	onStack[current] = True
        ids[current] = low[current] = id += 1
      
      # 인접노드를 모두 방문하고 low-link value를 갱신한다.
       for adjNode in graph[current]:
          if ids[adjNode] == UNVISITED: dfs(adjNode)
          if onStack[adjNode]: low[current] = min(low[current], low[adjNode])
          
      # current의 모든 인접노드를 방문하고 나서 
      # 현재 노드가 SCC의 시작지점인지 확인한다
      # 시작 지점이라면 스택에 있는 모든 노드들을 시작지점까지 꺼낸다
      if ids[current] == low[current]:
      	node = stack.pop()
      	while node == current:
        	onStack[node] = False
            	low[node] = ids[current]
            	node = stack.pop()
        sccCount += 1
        	
        

문제