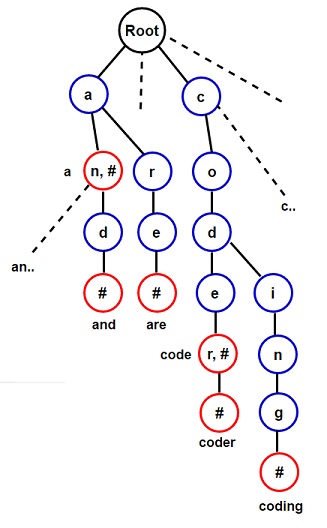
Trie

SeungHyuk Shin·2021년 6월 1일

Trie?

Trie는 문자열을 빠르게 탐색할 수 있게해주는 트리형 자료구조이다.루트 노드가 되는 가장 최상위 노드에는 어떠한 단어도 들어가지 않고, 루트 아래 노드부터 문자열들의 접두사가 하나씩 나타나게 된다. 이러한 특징 때문에 트라이는 접두사 트리(Prefix Tree) 라고도 불린다.

시간복잡도는 삽입,조회 모두 문자열의 길이가 M이라고 했을때 O(M)만큼의 시간복잡도를 가지게 된다.

하지만 트라이의 치명적 단점은 공간 복잡도에서 나타난다. 왜 공간 복잡도가 치명적인 단점이 되냐면,트라이에서 저러한 O(M)인 시간이 나오기 위해서는 다음 문자를 가리키는 노드가 필요하다.

예를들어 문제에서 숫자에 대해 트라이를 형성해야 한다면 0~9인 총 10개의 포인터 배열을 가져야한다.

또는 알파벳에 대해 트라이를 형성해야 한다면 a~z인 총 26개의 포인터 배열을 가지고 있어야한다.

즉 최종 메모리는 O(포인터 크기 포인터 배열 개수 트라이에 존재하는 총 노드의 개수)가 된다.

시간복잡도 O(M)

struct Trie{
    Trie* Node[26]; //알파벳 숫자
    bool finish; // 문자열이 끝났는지 확인
    bool nextChild; // 문자열의 자식이 있는지 확인

    // 생성자
    Trie(){
        fill(Node, Node + 26, nullptr);
        finish = nextChild = false;

    }
    //소멸자
    ~Trie(){
        for (int i = 0; i < 26; i++)
            if (Node[i])
                delete Node[i];
    }

    int tonum(char c) {        //문자를 숫자로 변환.
        return tolower(c) - 'a';    //대문자인 경우는 소문자로 변환.
    }

    void insert(const char* words) {
        if (*words == '\0'){ //입력받은 words가 '\0'일 경우, 즉 문자열 끝인 경우.
            finish = true;
            return;
        }       
 
        int next = tonum(*words);
 
        if (Node[next] == NULL) {
            Node[next] = new Trie();
            nextChild = true;
        }
        Node[next]->insert(words + 1); // 문자열의 주소 + 1
    }

    bool find(const char* words) {
        int next = tonum(*words);
 
        if (*words == '\0')
            return true;
 
        if (Node[next] == NULL)
            return false;
 
        return Node[next]->find(words + 1);
    }


};