문제

https://www.acmicpc.net/problem/29619 - 나무나무나 심어야지 (P3)

문제 요약

임의 형태로 구성된 트리 그래프가 있습니다.
해당 그래프의 Root는 1번 정점이고, 트리의 각 정점에는 0~500사이의 가중치가 부여되어 있습니다.
(뿌리가 1번이라는 설명은 Root가 1번 정점이라는 것을 아주 약하게 숨겨둔 것입니다.)

본 문제에서는 해당 트리에 두 가지 쿼리를 수행 해야합니다.

1. 1 i j w : i번 정점에 j번 정점을 새로 생성해 연결합니다. 이때 j번 정점에는 w의 가중치가 부여됩니다.

2. 2 i i번의 서브트리에 있는 정점들의 가중치 합을 출력합니다.

풀이

1번 쿼리는 조금 이후에 보고, 먼저 2번 쿼리를 처리하겠습니다.

2번 쿼리

최초 접근

Root가 1번으로 고정되어있기에 최초 한번의 BFS를 통해 각 정점의 부모 정점은 몇 번인지, 서브 트리를 구성하는 자식 정점은 몇 번인지 기록할 수 있습니다.

만약, 가중치 합을 물어보는 2번 쿼리가 딱 한번만 있었다면 주어진 i번 째 정점에서 자식 정점 방향으로 BFS를 돌려 답을 구할 수 있습니다.

하지만, 본 문제에서는 2번 쿼리가 최대 10만번 주어질 수 있습니다. N(트리의 정점의 수) + M(쿼리의 수)가 10만이기에 N과 M에 골고루 5만씩을 분배해둔다면 5만 크기의 BFS를 최대 5만번 돌려야하는 상황이 발생합니다. 이는 시간초과를 발생시킵니다.

그렇다면 저희는 임의의 정점의 서브 트리 가중치 합을 빠르게 구할 수 있는 방법을 찾아야합니다.

오일러 투어 테크닉(ETT)

만약 트리를 구간으로 만들 수 있다면, 구간 합을 구하는 방법을 통해 매우 빠르게 가중치 합을 구할 수 있게 됩니다.
트리를 구간으로 만들기 위해서는 오일러 투어 테크닉을 활용하게 됩니다.

오일러 투어 테크닉은 다음과 같이 진행됩니다.

1. Count 변수를 선언한다. 최초 값은 0이다.
2. 정점 개수 만큼의 in배열과 out 배열을 선언한다.
3. Root부터 BFS를 시작한다.
4. BFS를 하면서 in[nodeNumber]에 아직 값이 없다면, Count를 1 증가 시키고 in[nodeNumber]에 Count를 대입한다.
5. 만약 모든 서브트리를 방문하여 해당 정점에서 빠져나가게 된다면 out[nodeNumber]에 Count를 기록한다.

이렇게만 봐서는 어떻게 굴러가는지 잘 모르겠습니다. 그렇기에 본문에 나온 예제로 한번 봐보겠습니다.

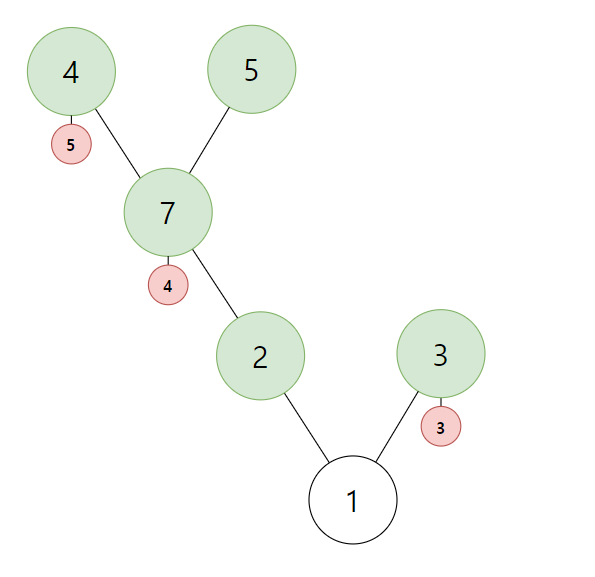
이러한 트리 그래프가 있습니다. (빨간 정점은 가중치를 나타내기에 무시해도 됩니다)

일단 in과 out, count를 만들어두고 이 트리의 Root인 1번 부터 BFS를 돌립니다.

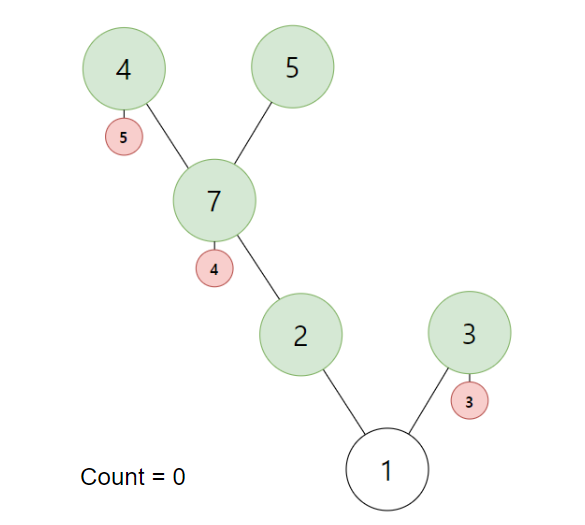
1번 정점에는 in값이 없습니다. 그렇기에 Count를 1로 증가시키고 in에 집어 넣습니다.

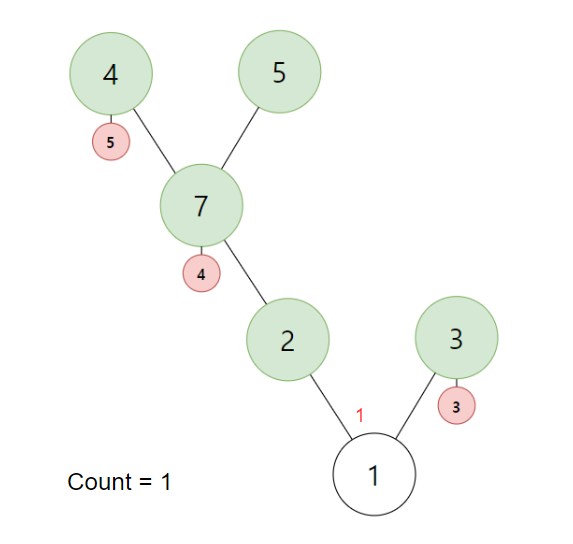
이후 BFS를 하며 서브트리로 계속 진행합니다.

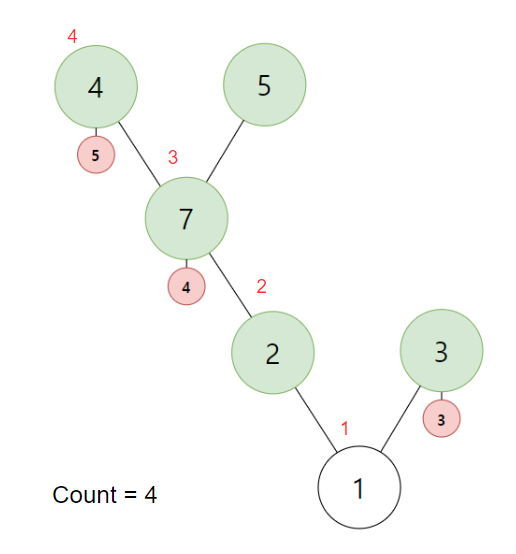
4번 정점까지 Count가 4입니다. 이제 BFS를 계속 해야하는데 정점에 서브 트리가 없습니다. 그렇기에 4번 정점에서 빠져 나갑니다. 이때 정점을 빠져나가기에 out에 Count를 기록합니다.

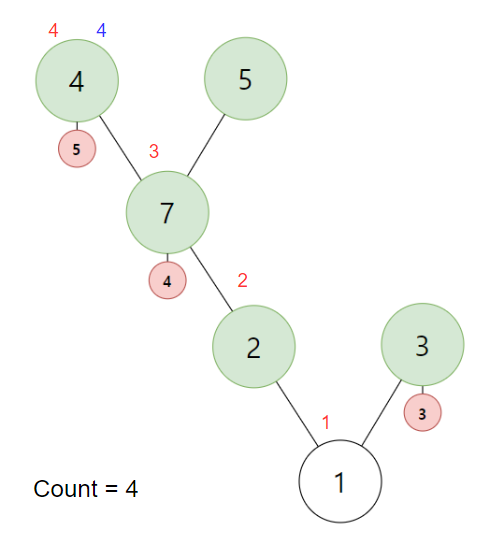
7번 정점의 경우 아직 탐색할 5번 정점이 있습니다. BFS를 계속 진행합니다. 5번의 in에는 아직 값이 없기에 Count가 증가하고 5의 값이 대입됩니다. 그리고 5번 또한 4번처럼 정점을 빠져 나오기에 out에 5가 대입됩니다.

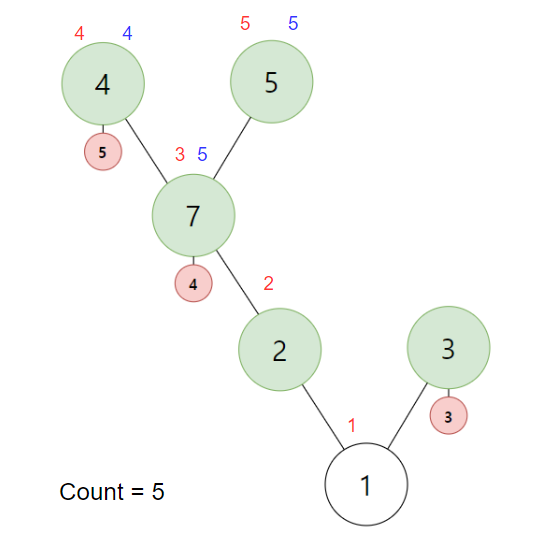
이후엔 7번 정점 또한 빠져나오기에 out에 5가 대입됩니다.

이를 모든 노드에서 반복하면 다음과 같은 결과가 나옵니다.

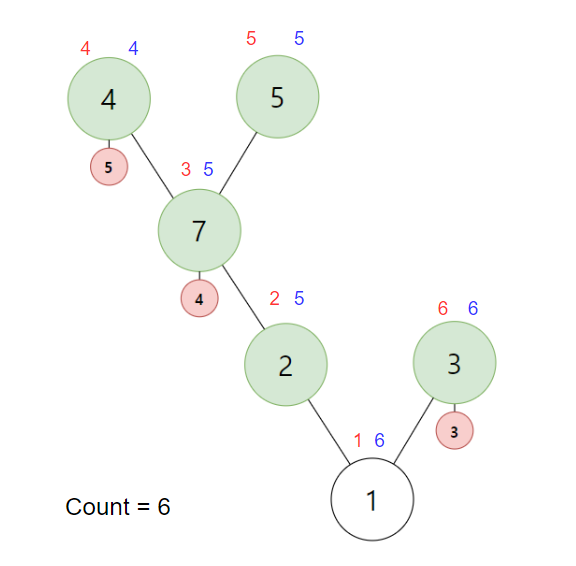
자 이제 in과 out를 사용하여 구간 합을 할 수 있게 됩니다.

4번 정점의 서브트리의 합 -> in[4] = 4, out[4] = 4
-> [4,4] 구간 합 구하기

7번 정점의 서브트리의 합 -> in[7] = 3, out[7] = 5
-> [3,5] 구간 합 구하기

1번 정점의 서브트리의 합 -> in[1] = 1, out[1] = 6
-> [1,6] 구간 합 구하기

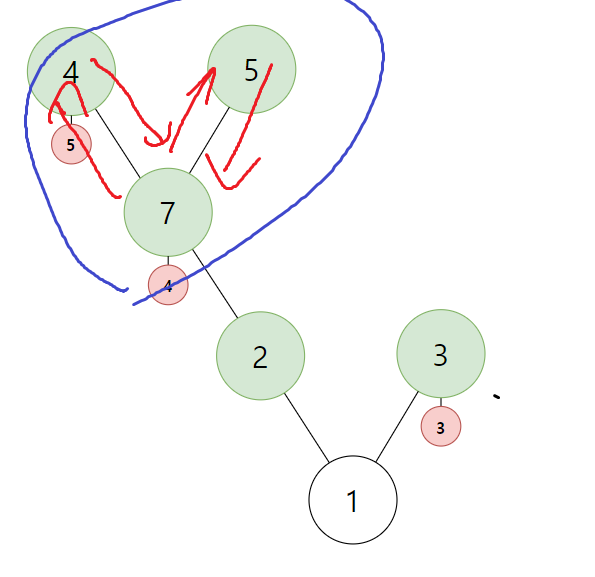
이 방식이 가능한 것은 위 그림과 같이 BFS 특성상 순회가 순차적으로, 무조건 현재노드 방문 -> 서브트리 방문 순서로 이어져 Count 번호를 부여받은 순서로 봤을때[현재 정점] 다음으로 연속해서 [서브트리 정점들 .... ] 이 모든 정점에서 성립하기 때문입니다. 이를 말로하면 잘 안보이는데 Count별 정점 번호를 실제로 표로 그리면 잘 보입니다.

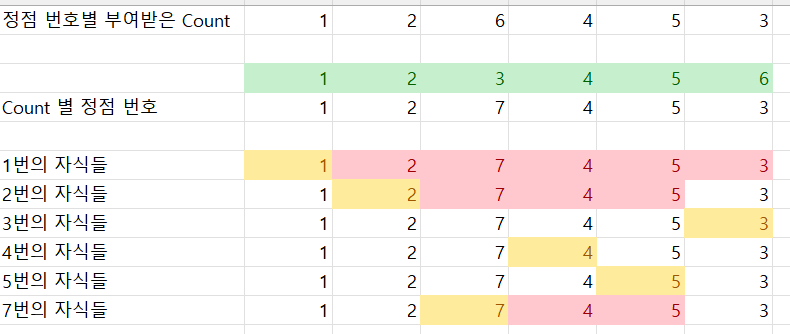
무조건 자식 서브트리의 정점들은 연속하게 존재합니다.

이렇게 구간합으로 만든 후에는 구간 합을 구하는 무언가를 쓰면 됩니다.

1번 쿼리

일단 1번 쿼리에는 두가지 역할이 있습니다.
1. 임의의 정점 추가
2. 가중치 증가

우리는 위에서 2번 쿼리를 ETT로 할 수 있다는 것을 알았습니다.

그런데 1번 쿼리는 그래프의 형태를 변경합니다 그렇기에 위에서 만든 ETT가 무력화되는 현상이 발생합니다. ETT는 그래프의 형태가 바뀌면 in, out 값이 다 바뀌고 이를 반영할 수 없습니다.

만약, 정점의 삭제 연산이 있었다면 이는 골치 아팠을 문제입니다. 하지만 이 문제에서는 트리는 1번 쿼리가 진행될 때마다 무조건 확장되게 됩니다. 즉 트리가 쿼리 도중 작아지지 않고, 2번 쿼리는 정점의 연결 유무와 무관하게 가중치의 존재 여부로 값이 결정됩니다.

그렇기에 우리는 모든 1번 쿼리를 미리 받아두고 트리를 먼저 구성해 둘 수 있습니다. 이렇게 되면 트리가 변하지 않기에 ETT로 구간 합을 구하는 것이 가능해집니다.

이렇게 쿼리를 미리 받아두고 후에 처리하는 것을 오프라인 쿼리라 합니다.

아무튼 이제 그럼 1번 쿼리는 임의의 정점에 가중치를 추가하는 연산으로 바뀌게 됩니다.

값이 바뀌는 구간합을 구하는 것은 세그먼트 트리를 통해 쉽게 할 수 있습니다.

이제 쿼리대로 진행하면 됩니다!

출제 의도

학교 대회 특성상 보통 이 정도 난이도까지 학생들이 풀진 않을 것이라 생각하여 후에 에디토리얼을 보고 아 이런게 가능하구나 이런 알고리즘도 있구나! 알리는게 목적이였습니다.

그렇기에 문제도 오프라인 쿼리, ETT, 세그트리등 여러개가 섞여있지만 그다지 어려운 문제는 아닙니다. 연습용으로 좋죠!