제가 낸 문제 중 가장 높은 난이도인 다이아 5를 가지는 문제입니다.
원래 다이아5라고 사람들이 안푸는건 아닌데, 문자열이라는 특성때문에 지금까지 출제, 검수 제외하고 딱 1명이 푼 비운의 문제입니다.
여기에 풀이를 적음으로서 사람들이 좀 더 풀어보기를 바래봅니다.
지문 해석
일단 지문의 가장 핵심만 요약하면 다음과 같습니다.
편지에는 N장의편지지가 존재합니다.- 이 N장의
편지지중 M장이 누락되었습니다. 하지만 N장 중 어떤편지지가 누락된지는 알 수 없습니다. - 근성이 원래
편지지에 이름을 등장시켜 고마움을 전달하고자 한사람이 K명 있습니다. - 하지만
편지에서 M장이 누락되었기에 각각 1, 2, 3 ... Ki번사람의 이름이편지에 등장하는지(고마움이 전달되는지) 알 수 가 없습니다. - 그렇기에 근성은
편지에 이름이 등장하는 것을 다음과 같이 정의합니다.- 이름이
편지지1장에 온전하게 등장한다. - 이름이 연속된
편지지에 나누어 등장한다. - 이름이 임의의
편지지가 누락되어 연속하게된편지지에 나누어 등장한다.
- 이름이
- 이 예는 아래와 같습니다.

- N장의
편지지중 어떤 경우의 수로 M장의편지지가 누락되어도편지에 특정사람의 이름이 등장한다면 그사람에게 고마움이 전달됩니다. - 누구에게 고마움이 전달되는지 구해봅시다.
이 문제를 왜 푸는 사람이 적은지 알 수 있습니다.
어쨌든 핵심만 보자면 "K개의 이름 각각에서 N개의 편지지에서 정해지지 않은 M개의 편지지를 제거한 후 내용을 모두 합쳤을 때 항상 이름이 등장하는지 판단해라"입니다.
제한은 다음과 같습니다.
- 편지지 개수(N) =
2이상450이하 - 누락된 편지지(M) =
1이상N - 1이하 - 각 편지지 내용의 길이(si) =
2이상450이하 - 이름의 개수(K) =
1이상450이하 - 각 이름의 길이(ki) =
1이상min(si)이하
접근 및 풀이
단순
가장 단순하게 접근 할 수 있는 방법은 실제로 편지를 누락시켜 보는 것 입니다.
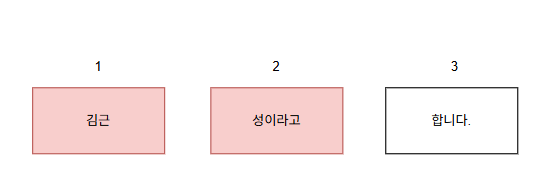
위와 같이 3장의 편지지가 있고 1장의 편지지가 누락되었다면
아래와 같이 동작합니다.
- 1번 편지지 제거 ->
성이라고합니다->김근성미등장 - 2번 편지지 제거 ->
김근합니다->김근성미등장 - 3번 편지지 제거 ->
김근성이라고->김근성등장
실제로 누락 시키고 합쳐보면 이름의 등장여부를 알 수 있습니다.
하지만, 좀 많이 느립니다.
N과 M이 있을때 이 방식은 K*(max(|N|)+max(|K|)*(N C M) (C는 조합) 의 속도로 동작합니다.
주어진 제한이 K, N, M, |N|, |K| 전부 450이기에 대충 N C M 만 계산해도 아래와 같이 나옵니다.
450 C 250 =
6798544160615574298311029816617183396019976476004683307082128609548025523317433088462142079898966986796135192955701072586970040095008
더 빠르게 해야합니다.
기본 - 1
문제의 제한을 보시면 아래와 같은 게 있습니다.
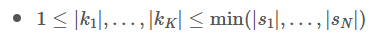
이 제한을 통해 이름의 최대 길이는 항상 편지지의 최소길이보다 작거나 같단 걸 알 수 있습니다.
즉, 이름이 나누어 등장하는 것도 최대 연속된 2개의 편지지에만 나누어 등장 할 수 있습니다.

(이름이 3개에 편지지에 나눠 등장하기 위해선 편지지의 최소 길이보다 이름이 길어야함)
그렇기에 이름의 등장을 확인하기 위해 모든 편지지 제거를 고려하여 조합을 계산한 후 합쳐볼 필요가 없습니다.
이름의 등장은 어떤 편지지 i와 그 뒤에 나오는 j편지지의 조합 또는 i, j 그 자체에서만 나올 수 있기 때문입니다.

우리는 이제 편지지개수인 N만큼 돌며 해당 편지지를 선택했을때 이름이 생기는지 보면 됩니다.
위와 같은 경우 근성을 찾으려 할때
- 파랑은 이름이 생기지 않습니다.
- 초록은 이름이 자체에 포함되어있습니다.
- 빨강은 파랑과의 조합 혹은 초록 자체에 포함된 것으로 이름이 생깁니다.
위와 같이 N^2으로 이름의 등장을 찾을 수 있게 됩니다.
하지만, 맹점이 있습니다. 위에서 파랑과의 조합으로 이름이 생기는 것은 파랑과 빨강이 연속되었음을 가정하는 것입니다.
즉, 초록이 누락되었을때(제거되었을때) 이름이 조합으로 생깁니다. 이는 파랑과 빨강의 조합을 확인하기위해 그 사이에 있는 모든 편지지의 누락을 가정해야함을 의미합니다.
그럼에도 만약 한가지라도 등장하는 경우를 찾는거라면 그냥 파랑 이전까지 1~M가 누락되었다를 하나의 축으로 더 만들어 3차원 DP를 돌리면 되기에 쉽게 구할 수 있습니다.
그런데 모든 누락경우에서 등장하는지 확인해야하는 본 문제에서는 누락 상태또한 저장해야하고 이는 시간복잡도, 공간복잡도가 너무 커지게 됩니다.
이 상태를 제거할 수 없을까요?
기본 - 2
가장 오래걸리고 복잡한 상태인 누락 상태를 제거해야합니다.
지금 누락 상태가 복잡한 이유는 어떠한 M개 누락에 대해 이름이 등장하는지 찾아야하기 때문입니다.
이를 좀 더 자세히 표현하면 아래와 같습니다.
N개의 편지지 중 어떤 M개의 편지지를 제거해도 편지지의 내용을 합친 문자열에 이름이 들어간다.
M개의 편지지를 제거했을때 이름이 들어간다는 것은 M보다 작은 개수의 편지지를 제거해도 이름이 들어가게 됩니다.
또, N개의 편지지 중 M개 이하를 제거한다는 것은 역으로 N개의 편지지중 N-M개를 고르는 것과 같습니다. 그렇기에 아래와 같이 변형할 수 있습니다.
N개의 편지지 중 어떤 N-M개 이상의 편지지를 골라도 편지지의 내용을 합친 문자열에 이름이 들어간다.
그리고 이는 자연스럽게 아래와 같이 구할 수 있습니다.
골랐을때 이름이 생기지 않는 편지지만 남겨도 N - M개 보다 적다
이제 이름이 생기지 않는 선에서 최대한으로 편지를 고르는 문제로 바뀌었습니다.
이름이 생기는 조건은 위에서도 보았듯 두가지 입니다.
- 이름이 편지지에 포함됨.
- 두 편지지를 합쳤을때 이름이 생김
그럼 바뀐 문제에 맞게
- 이름이 포함된 편지지는 고를 수 없다.
- i번째 편지지를 선택할지 고려중일때 i보다 작은 j번째 편지지를 확인하여 이름이 만들어지면 j뒤에는 i가 올 수 없다.
이 두가지를 고려해 최대 몇개의 편지지를 고를 수 있는지 보면 됩니다.
이는 위에서와 같이 i,j 두개의 편지지만 확인하고 만약 가능하다면 i까지 가능한 최대 편지지 개수 + 1을 j에 저장하는 방식으로 이중 for문을 통하여 구할 수 있습니다.
for(int i = 2;i<=n;i++){
for(int j = 1;j<i;j++){
if(편지지 포함) continue;
if(편지지 합쳐서 생김) continue;
dp[j] = max(dp[j], dp[i]+1);
}
}여기까지 왔다면 시간복잡도는 N^2 * (max(|ki|) + max(|si|)* k 가 걸립니다.
주어진 제한에서 이는 820억이 나오고 아직도 너무 크기에 더 줄여야합니다.
심화 - 1
여기서 더 줄일 수 있는 부분은 이름의 등장을 판별하는 부분입니다.
편지 2개를 고르고 두 편지를 합쳐 이름의 등장 여부를 판단하는 것을 너무 느립니다.
그렇기에 각 편지에서 이름의 등장 가능성을 확인해야하는데, 또 그것을 구한 이후 두 편지를 합쳐서 이름이 등장하는지를 빠르게 확인해야합니다.
이름이 두 편지에 나눠 등장하는 경우를 봐보겠습니다.
geunseong 기준
[ geunseong/ ][ geunseon/g ] [geunseo/ng] … [ g/eunsong ][ /geunseong ]
이는 앞쪽 편지지에 geunseo, 뒤쪽 편지지에 ng 가 등장하면 두 편지지가 합쳐져 geunseong이 나옴을 의미합니다.
앞쪽 편지지에서 geunseong, geunseon, geunseo, … ge, g, ‘ ‘ 즉 prefix들이 등장하는지 구해두고
뒤쪽 편지지에서 ‘ ‘ , g, ng, ong, … unseong, eunseong, geunseong, 즉 suffix들이 등장하는지 구해두면 이를 합쳐 이름의 등장 여부를 빠르게 구할 수 있습니다.
이렇게 각 길이에 해당하는 prefix, suffix를 구하는데에는 Z를 사용할 수 있습니다.
Target = name + “$” + letter로 두었을때 이 target으로 z를 돌리면 z에 name과 일치하는 prefix의 최대길이가 저장됩니다.
1 <= i <= | name | 일 때 만약 z[ | target | – i ] 에 i가 저장되어있다면 name의 앞에서부터 i 글자가 letter의 끝에 등장한다는 뜻이 됩니다.

위 이미지에서 z[target-4] 에는 4가 저장되어있습니다. 즉 target의 접미사에 BBBA가 등장한다는 것이고 만약 이후 다른 곳에서 접두사에 AB가 있는 편지가 있다면 둘이 합쳐 이름이 만들어집니다.
마찬가지로 suffix또한 구할 수 있습니다.
Target = letter + “$” + name 로 두었을 때 이 target으로 z를 돌리면 z에 letter과 일치하는 prefix의 최대길이가 저장됩니다.
1<= i <= | name | 일때 만약 z[ | target | - i ] 에 i가 저장되어있다면 name의 뒤에서부터 i글자가 letter의 시작에 등장한다는 뜻이 됩니다.
Prefix[i]에 i길이의 prefix가 있는지, suffix[i]에 i길이의 suffix가 있는지 저장합니다.
하지만, 이렇게 prefix, suffix를 구하더라도 조합을 확인하는데 결국 | name | 만큼 확인을 해야합니다. (위의 근성의 조합확인을 위해 근성의 길이 만큼 돌아봄)
좀 더 빠르게 할 방법이 없을까요?
심화 - 2
prefix와 suffix를 비트셋에 저장하게 되면 비트셋 끼리의 AND 연산으로 한번에 비교가 가능해집니다.
이를 위해 suffix의 저장되는 방식을 조금 바꿉니다.
Prefix[i]와 매칭되는 것은 suffix[ |name| - i ] 입니다.
같은 자리의 비트끼리 연산이 되는비트연산의 특성을 고려하여 suffix를 저장할 때부터 suffix[i]에 | name | - i 길의의 suffix가 있는지 저장한다면 prefix[i]와 suffix[i]의 매칭을 비교하면 되고 !(suffix & prefix).any() 와 같은 비트셋끼리의 연산 한번으로 이름의 존재여부를 알 수 있게 됩니다.
비트셋의 연산수는 비트길이/컴퓨터의 워드 단위 입니다.
채점환경에서는 비트길이/64, 즉 |name|/64가 나옵니다.
이름과 편지지의 조합을 미리 확인하기에 해당 작업은 이름과 편지를 모두 받은 뒤 진행해야합니다.
또 prefix를 구하는 과정에서 만약 max(z[i])가 | name | 라면 해당 편지지에 이름이 온전하게 등장하는 것이기에 이후 dp에서 빠르게 건너뛰기위해서 skip 등의 플래그로 표시해줍니다.
마무리
이제 빠르게 이름의 등장여부를 확인할 수 있게 되었기에 비트셋과 skip을 이용하여 위에서 보았던 dp를 돌리면 됩니다.
시간 복잡도는 O(K*N*(2ki + si) + N*K*(2ki + si) + K*N^2*si/64)로 총 O(K*N^2*si/64) 가 나옵니다.
대략 O(N^4 / 64)네요!
마무리하며
상당한 난이도의 문제로 저도 몰라서 검수진의 도움을 많이 받았습니다. 다들 한번 풀어보기를...
