내가 낸 문제 내가 풀어보기 / 34403- 코딩하는 근성도 바리스타입니다(P4)

본문

링크

쉽게 요약하자면 최초에 $C$ 만큼의 농도를 가지는 아메리카노가 $L$만큼 있습니다.

또한 이 아메리카노에는 최초에 $S$ 만큼의 얼음이 동동 떠있습니다.

이제 매 1분마다 다음과 같은 두 과정이 일어납니다.

아메리카노를 마시거나 / 그대로 두거나

만약 아메리카노의 농도가 $c_{max}$ 이하, $c_{min}$ 이상이라면 아메리카노를 마실 수 있습니다.
마시면 아래와 같은 변화가 일어납니다.

$L = L - E$

만약 마시지 않으면 아무 변화도 일어나지 않습니다.

얼음이 녹는다.

아메리카노를 마실지 말지 결정한 뒤 얼음이 녹습니다.
얼음이 녹으면 다음과 같은 변화가 일어납니다.

$L = L + M$
$S = S - M$
$C = C * \frac {L}{L + M}$

이때 $S$는 $M$의 배수이기에 얼음이 $M$보다 작게 녹는 일은 없고, 얼음이 다 녹으면 농도 변화가 멈춥니다.

여기서 저희는 마실 수 있는 아메리카노의 최대 양을 구해야합니다.

접근

마심

먼저 농도 변화를 봐보겠습니다.

문제에서 농도는 $C = C * \frac {L}{L + M}$ 형태로 변화하게 됩니다. 이 식대로라면 같은 농도일때 L이 작아지면 작아질수록 농도 변화가 커지게 됩니다.

또한 L을 변화시키는 것은 항상 발생하는 얼음 녹음과 선택적으로 가능한 마심이 있습니다.

얼음 녹음은 매 분마다 항상 생기기에 고정이고, 저희는 여기서 마심을 하면 할 수록 농도가 더 빨리 떨어지게 된다는 걸 알 수 있습니다.

케이스 분리

앞서 마심은 농도를 더 빨리 떨어지게 한다 하였습니다.
그렇다면 마심을 하나도 하지 않은 상황은 농도를 가능한 늦게 떨어지게 만들고 최종적으로 얼음이 모두 다 녹았을때 가능한 가장 높은 농도를 만들어냅니다.

그럼 이 농도로 케이스 분리가 가능합니다.

1. 얼음이 다 녹았을때 농도가 $C_{max}$초과이다.
이 경우 얼음이 다 녹아도 농도 밖이기에 마실 수 없습니다. 또한 농도를 더 빨리 떨어트리고 싶어서 마심을 하려해도 농도 범위 밖이기에 불가능합니다.

2. 얼음이 다 녹았을때 농도가 $C_{max}$이하 $C_{min}$이상이다.
이 경우 아메리카노의 원래 양($L$) + 얼음이 녹은 양($S$)을 모두 마실 수 있습니다. 얼음이 다 녹기전에 마심은 오히려 농도를 $C_{min}$보다 떨어지게 할 수 있기에 항상 최적이 아닙니다.

2. 얼음이 다 녹았을때 농도가 $C_{min}$미만이다
이 경우 그냥 둬도 농도 범위를 벗어납니다. 그렇기에 적절한 타이밍에 마심을 하여 최적의 답을 구해야합니다.

1번과 2번은 답이 0과 L+S로 바로 구할 수 있습니다.
아예 마심을 하지 않는 경우이기에 $C = C * \frac {L}{L + M}$ 를 $S/M$ 번 적용하여 다 녹았을때의 농도를 구하고 판단하면 됩니다.

실수 연산

문제에서 농도 변화는 소수점 10번째 자리에서 버려진다고 하였습니다.

사실 농도 변화 계산은 그냥 실수로 구하게 되면 부동소수점 오차로 인하여 답이 달라지게 됩니다.

그렇기에 이 실수 오차를 없애야합니다.

이는 문제에서 모든 실수가 소수점 9번째 자리까지만 주어진다하였기에 모든 실수에 $10^9$를 곱하여 정수로 변환함으로서 해결 가능합니다.

또한 이렇게 되면 농도 계산식인 $C = C * \frac {L}{L + M}$ 또한 정수로 변환한 $C$에 $L$을 곱하고 $(L + M)$ 으로 나눠주는 식으로 구할 수 있게되고 해당 값을 정수 변수에 집어넣게 되면 자동으로 소수점이 버려져 10번째 자리 버림또한 별 연산 없이 구현 가능해집니다.

3번 케이스

이제 실수연산을 제거하였고, 1,2번 케이스를 처리하였습니다.

그럼 3번 케이스를 구해보겠습니다.

일단 3번의 경우 농도가 일단 범위 안으로 들어오게 되면 그 안에 있는 동안에는 언제든지 먹을지 안먹을지를 선택할 수 있습니다.

또한 이 특정 분에 결정한 마심은 해당 분부터 이후의 농도 변화의 속도를 누적시킵니다.

$C = C * \frac {L}{L + M}$

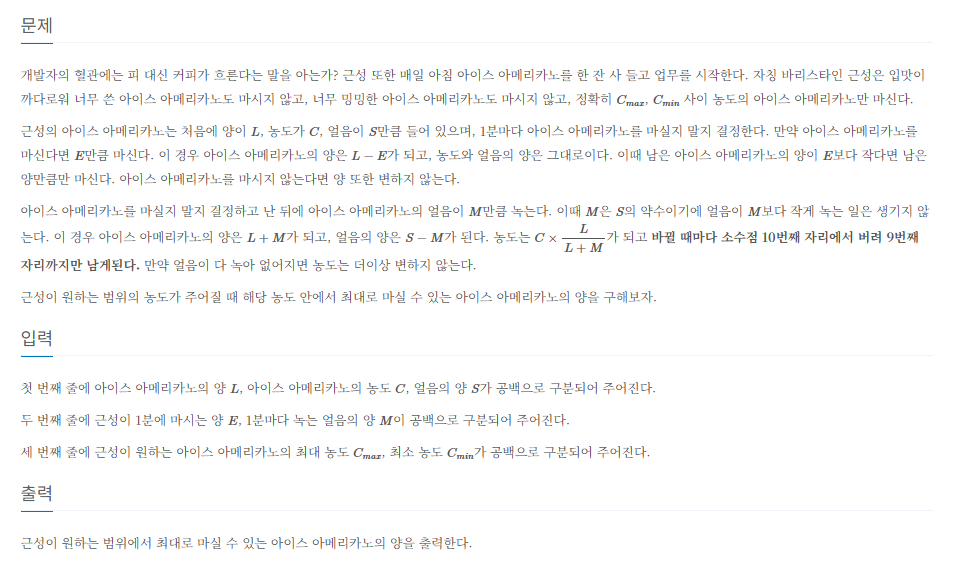
즉 마시는 시점의 경우에 따라 매 분의 농도가 달라집니다.

이 경우는 매우 많기에 ($2^{S/M}$) 모두 구할 수 없습니다.

농도 범위에서 유지하기

저희는 농도 범위안에서 최대한 많은 양을 마시는 것이 목적입니다.

이는 바로 농도 범위를 최대한 유지시키는 것이 목적이라는 것을 의미합니다.

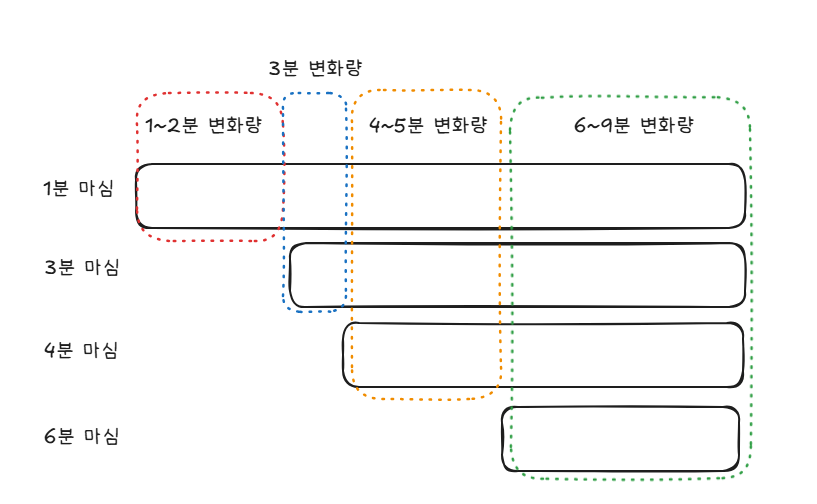
일단 저희가 연속된 2분 중에 한번만 마시는 경우를 생각해보겠습니다.

이 두경우의 농도 변화는 아래와 같이 표현됩니다.

마시고, 쉼 -> $C \times \frac{L -E}{L -E + M} \times \frac{L-E+M}{L-E+2M}$ -> $C \times \frac{L-E}{L-E+2M}$

쉬고, 마심 -> $C \times \frac{L}{L+M} \times \frac{L-E + M}{L-E + 2M}$

이를 통해 두 값의 비율을 비교해보겠습니다.

$\frac{쉬고, 마심}{마시고, 쉼}$ -> $\frac{C \times \frac{L}{L + M} \times \frac{L-E+M}{L-E+2M}}{C \times \frac{L-E}{L-E+2M}}$

=> $\frac{\frac{L}{L + M}\times (L-E+M)}{L-E}$

=> $\frac{L \times (L-E+M)}{(L-E) \times (L + M)}$

=>$\frac{L^2 -LE+LM}{L^2 - LE + LM - EM}$

분모에 $-EM$이 붙기에 분자보다 분모가 더 작습니다. 즉, 이 값은 1보다 크고 이는 쉬고,마심의 농도가 마시고, 쉼보다 큼을 의미합니다.

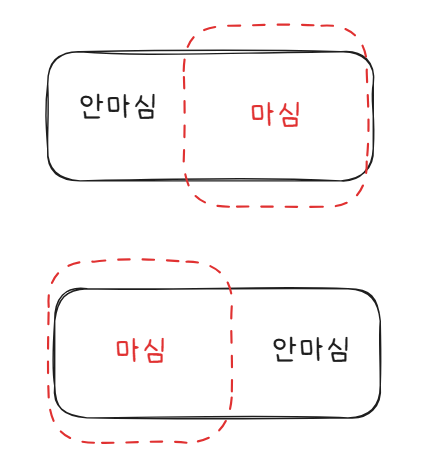
만약 현재 농도가 농도 범위안에 있다면 농도가 떨어지는 것을 최대한 늦추는것이 이득이니 저희는 마심을 미룰 수 있다면 최대한 미뤄야함을 의미합니다.

이는 모든 마심에 적용되기에 최종적으로 K번 마심을 진행한다면 K을 최대한 끝까지 미뤄 K번 마신 이후에 바로 농도 범위를 벗어나도록 하는 것이 최적입니다.

답 구하기

이제 결국 K번을 최대한 마지막에 마셔야합니다.

그런데 정작 K가 몇인지, 몇 분 부터 마셔야하는지 알 수 없습니다.

이때 S/M이 최대 1만이기에 1~ S/M인 매 분에 대해 연속으로 계속 마심을 시도하고 농도 범위를 벗어나면 탈출하는 식으로 최대로 마실 수 있는 양을 기록하면 답을 구할 수 있게됩니다.

시간 복잡도는 $O((S/M)^2)$이 나옵니다.

마무리하며

저 혼자서 생각해낸것 치고는 꽤 난이도 있고 퀄리티 좋은 문제가 나온 것 같습니다.

보기엔 단순 시뮬레이션 같아보이지만 꽤 발상을 요구하는거죠!

그래서 그런지 문제에 오답이 매우 많습니다.

다음에는 어떤 문제를 내볼까요!