1. 트리(tree)
데이터 사이의 계층 관계를 노드로 나타낸 자료구조
1-1. 트리 - 관련 용어
-
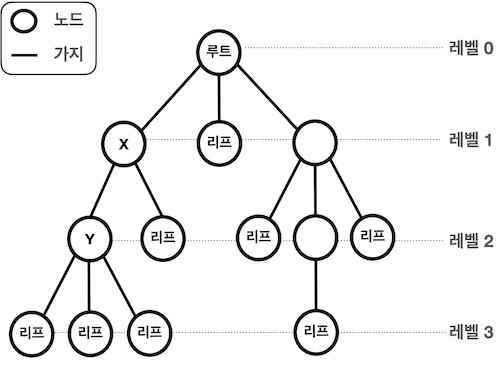
루트
트리의 가장 윗부분에 위치하는 노드를 루트(root)라고 한다. 하나의 트리에는 하나의 루트가 존재한다.
-
리프
트리의 가장 아랫부분에 위치하는 노드를 리프(leaf)라고 한다.
가장 아랫부분의 의미는 물리적으로 가장 아래가 아닌 더 이상 뻗어나갈 수 없는 마지막 노드의 위치를 의미 -
안쪽 노드
루트를 포함하여 리프를 제외한 노드를 안쪽 노드라고 한다.
-
자식
어떤 노드로부터 가지로 연결된 아래쪽 노드를 자식(child)이라고 한다.
노드는 자식을 여러개 가질 수 있다. 예를 들어 X는 2개의 자식, Y는 3개의 자식을 가지고 있다.
-
부모
어떤 노드에서 가지로 연결된 위쪽 노드를 부모(parent)라고 한다.
노드는 1개의 부모를 가진다. 예를 들어 Y의 부모는 X이다.
-
형제
같은 부모를 가지는 노드를 형제(sibling)라고 한다.
-
조상
어떤 노드에서 가지로 연결된 위쪽 노드를 모두를 조상(ancestor)이라고 한다.
-
자손
어떤 노드에서 가지로 연결된 아래쪽 노드 모두를 자손(desendant)이라고 한다.
-
레벨
루트로부터 얼마나 떨어져 있는지에 대한 값을 레벨(level)이라고 한다.
루트의 레벨은 0이고 루트로부터 가지가 하나씩 아래로 뻗어나갈 때 마다 레벨이 1씩 증가한다.
-
차수
노드가 갖는 자식의 수를 차수(degree)라고 한다.
예를 들어 X의 차수는 2, Y의 차수는 3이다. 모든 노드의 차수가 n 이하인 트리를 n진 트리라고 한다.
예제 트리는 모든 노드의자식이 3개 이하이므로 3진 트리이다.
-
높이
루트로부터 가장 멀리 떨어진 리프까지의 거리(리프 레벨의 최댓값)를 높이(height)라고 한다.
예제 트리의 높이는 3이다.
-
서브 트리
트리 안에서 다시 어떤 노드를 루트로 정하고 그 자손으로 이루어진 트리를 서브 트리(subtree)라고한다.
-
널 트리
노드, 가지가 없는 트리를 널 트리(null tree)라고 한다.
-
순서 트리와 무순서 트리
형제 노드의 순서가 있는지 없는지에 따라 트리를 두 종류로 분류한다.
형제 노드의 순서를 따지면 → 순서 트리(ordered tree)
형제 노드의 순서를 따지지 않으면 → 무순서 트리(unordered tree)
1-2. 순서 트리 탐색
순서 트리의 노드를 스캔하는 방법은 두 가지가 존재한다. 이진트리를 예로 살펴보자.
너비 우선 탐색(breadth-fisrt-search)
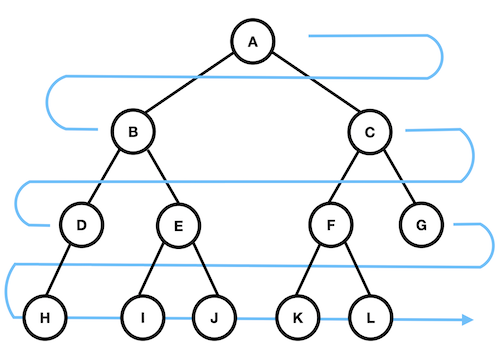
- 낮은 레벨에서 시작해 왼쪽 → 오른쪽 방향으로 검색한다.
- 한 레벨에서의 검색이 끝나면 다음 레벨로 내려간다.
- 검색 순서는 다음과 같다.
A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> K -> L
깊이 우선 탐색(depth-first-search)
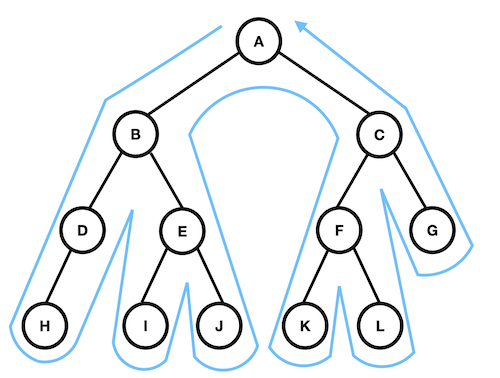
- 리프까지 내려가면서 검색하는 것을 우선순위로 하는 탐색 방법
- 리프에 도달해 더 이상 검색을 진행할 곳이 없는 경우 부모에게 돌아간다.
- 그 다음 다시 자식 노드로 내려간다.
깊이 우선 탐색의 경우 '언제 노드를 방문할지' 는 다음과 같이 세 종류로 구분한다.
전위 순회(Preorder)
- 노드 방문 → 왼쪽 자식 → 오른쪽 자식
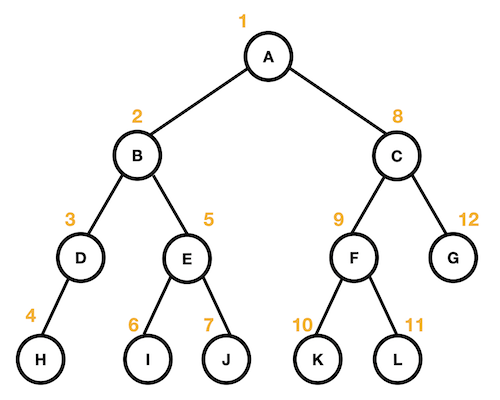
A -> B -> C -> H -> E-> I -> J -> C -> F -> K -> L -> G
중위 순회(Inorder)
- 왼쪽 자식 → 노드 방문 → 오른쪽 자식
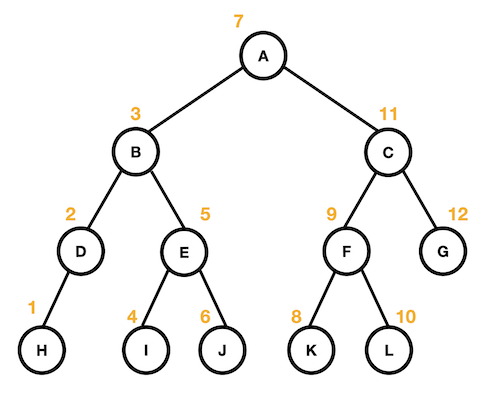
H -> D -> B -> I -> E -> J -> A -> K -> F -> L -> C -> G
후위 순회(Postorder)
- 왼쪽 자식 → 오른쪽 자식 → (돌아와) 노드 방문
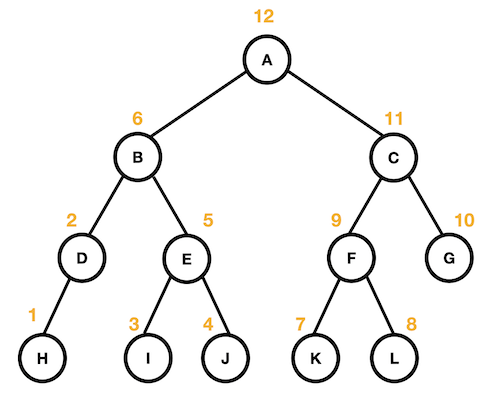
H -> D -> I -> J -> E -> B -> K -> L -> F -> G -> C -> A
1-3. 이진트리와 이진검색트리
이진트리
노드가 왼쪽 자식과 오른쪽 자식을 갖는 트리를 이진트리(binary tree)라고 한다.
- 각 노드의 자식은 2개 이하여야 한다.
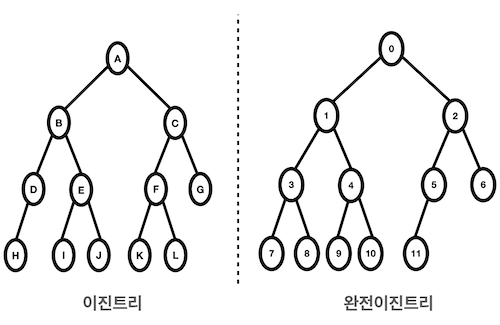
완전이진트리
루트부터 노드가 채워져 있으면서 같은 레벨에서 왼쪽 → 오른쪽 순으로 노드가 채워져 있는
이진트리를 완전이진트리(complete binary tree)라고 한다.
- 마지막 레벨을 제외한 레벨은 노드를 가득 채운다.
- 마지막 레벨은 왼쪽 → 오른쪽 방향으로 노드를 채운다. 반드시 끝까지 채울 필요는 없다.
- 완전이진트리에서 너비 우선 탐색을 하며 각 노드에 0, 1, 2 ... 값을 주면 배열에 저장하는 인덱스와
일대일로 대응한다. - n개의 노드를 저장할 수 있는 완전이진트리의 높이는 log n 이다.
이진검색트리(binary search tree)
이진검색트리는 이진트리가 다음 조건을 만족하면 된다.
- 어떤 노드 N을 기준으로 왼쪽 서브 트리 노드의 모든 키 값은 노드 N의 키 값보다 작아야 한다.
- 오른쪽 서브 트리 노드의 키 값은 노드 N의 키 값보다 커야 한다.
- 같은 키 값을 갖는 노드는 없다.
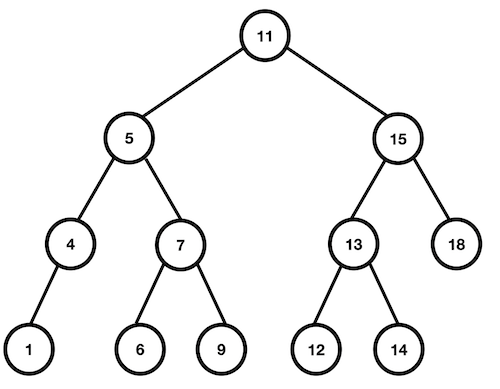
이진검색트리를 구현한 예시이다.
- 노드 5를 기준으로 보면 왼쪽 서브 트리 노드(4, 1)은 모두 5보다 작다.
- 오른쪽 서브 트리 노드(7, 6, 9)는 모두 5보다 크다.
이때 이진검색트리를 중위순회(Inorder)하면 다음과 같이 키 값의 오름차순으로 노드를 얻을 수 있다.
1 -> 4 -> 5 -> 6 -> 7 -> 9 -> 11 -> 12 -> 13 -> 14 -> 15 -> 18
1-4. 이진검색트리 구현 - Java 코드
public class BinTree <K, V> {
private Node<K, V> root;
private Comparator<? super K> comparator = null;
public BinTree() {
root = null;
}
public BinTree(Comparator<? super K> c) {
this();
comparator = c;
}
/** 두 키 값을 비교 */
private int comp(K key1, K key2) {
return (comparator == null) ? ((Comparable<K>)key1).compareTo(key2)
: comparator.compare(key1, key2);
}
/** 키에 의한 검색 */
public V search(K key) {
Node<K, V> p = root;
while (true) {
if (p == null)
return null;
int cond = comp(key, p.getKey());
if (cond == 0)
return p.getValue();
else if (cond < 0)
p = p.getLeft();
else
p = p.getRight();
}
}
/** node를 루트로 하는 서브 트리에 노드 <K, V>를 삽입 */
private void addNode(Node<K, V> node, K key, V value) {
int cond = comp(key, node.getKey());
if (cond == 0)
return; // key가 이진검색트리에 이미 있음
else if(cond < 0) {
if (node.getLeft() == null)
node.setLeft(new Node<>(key, value, null, null));
else
addNode(node.getLeft(), key, value); // 왼쪽 서브트리에 주목
} else {
if (node.getRight() == null)
node.setRight(new Node<>(key, value, null, null));
else
addNode(node.getRight(), key, value); // 오른쪽 서브트리에 주목
}
}
public void add(K key, V value) {
if (root == null)
root = new Node<>(key, value, null, null);
else
addNode(root, key, value);
}
/** 키 값이 key인 노드를 삭제 */
public boolean remove(K key) {
Node<K, V> p = root; // 스캔 중인 노드
Node<K, V> parent = null; // 스캔 중인 노드의 부모 노드
boolean isLeftChild = true; // p는 부모의 왼쪽 자식 노드인가?
while (true) {
if (p == null)
return false;
int cond = comp(key, p.getKey());
if (cond == 0)
break;
else {
parent = p;
if (cond < 0) {
isLeftChild = true;
p = p.getLeft();
} else {
isLeftChild = false;
p = p.getRight();
}
}
}
if (p.getLeft() == null) { // p에 왼쪽 자식이 없음
if (p == root)
root = p.getRight();
else if (isLeftChild)
parent.setLeft(p.getRight());
else
parent.setRight(p.getRight());
} else if (p.getRight() == null) { // p에 오른쪽 자식이 없음
if (p == root)
root = p.getLeft();
else if (isLeftChild)
parent.setLeft(p.getLeft());
else
parent.setRight(p.getLeft());
} else {
parent = p;
Node<K, V> left = p.getLeft(); // 서브 트리 가운데 가장 큰 노드
isLeftChild = true;
while(left.getRight() != null){
parent = left;
left = left.getRight();
isLeftChild = false;
}
p.setKey(left.getKey());
p.setValue(left.getValue());
if (isLeftChild)
parent.setLeft(left.getLeft());
else
parent.setRight(left.getLeft());
}
return true;
}
// node를 루트로 하는 서브 트리의 노드를 키 값의 오름차순으로 출력
private void printSubTree(Node node) {
if (node != null) {
printSubTree(node.getLeft()); // 왼쪽 서브 트리를 키 값의 오른차순으로 출력
System.out.println(node.getKey() + " " + node.getValue()); // node 출력
printSubTree(node.getRight()); // 오른쪽 서브 트리를 키 값의 오름차순으로 출력
}
}
// 모든 노드를 키 값의 오름차순으로 출력
public void print() {
printSubTree(root);
}
}public class Node<K, V> {
private K key;
private V value;
private Node<K, V> left;
private Node<K, V> right;
public Node(K key, V value, Node<K, V> left, Node<K, V> right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
// getter, setter
}2. 힙 (heap)
최대값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조
2-1. 우선순위 큐
- 우선순위의 개념을 큐에 도입한 자료구조
- 데이터들이 우선순위를 가지며, 우선순위가 높은 데이터가 먼저 나간다.
- 우선순위 큐의 이용 사례
- 시뮬레이션 시스템
- 네트워크 트래픽 제어
- 운영체제에서의 작업 스케쥴링
- 우선순위 큐는 배열, 연결리스트,
힙으로 구현이 가능하다. 이 중힙으로 구현하는 것이 가장 효율적이다.
2-2. 힙 이란?
- 완전이진트리의 일종이며, 우선순위 큐를 위하여 만들어진 자료구조
- 여러 개의 값 중 최대값과 최솟값을 빠르게 찾아내도록 만들어진 자료구조
- 힙에서 부모와 자식 관계는 일정하지만 형제 사이의 대소 관계는 일정하지 않음
- 힙 트리에서는 중복된 값을 허용 (이진탐색트리에서는 중복된 값을 허용하지 않음)
- 힙에서 가장 높은(혹은 가장 낮은) 우선순위를 가지는 노드가 항상 루트에 위치
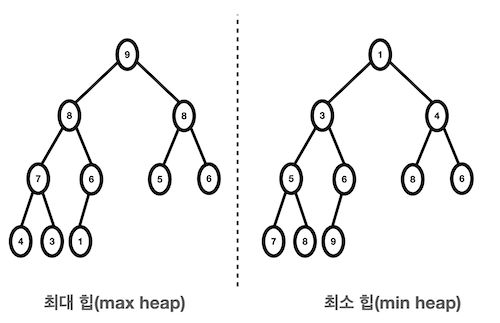
2-3. 힙의 종류
- 최대 힙(max heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전이진트리
- key(부모노드) ≥ key(자식노드)
- 최소 힙(min heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전이진트리
- key(부모노드) ≤ key(자식노드)
2-4. 힙 연산
- 배열을 이용하여 힙을 저장한다.
- 부모 노드와 자식 노드의 관계
- 부모 인덱스 = (자식 인덱스 - 1) / 2
- 왼쪽 자식 인덱스 = (부모 인덱스 * 2) + 1
- 오른쪽 자식 인덱스 = (부모 인덱스 * 2) + 2
힙의 삽입
- 힙에 새로운 요소가 들어오면, 새로운 노드를 힙의 가장 마지막 노드에 이어 삽입한다.
- 새로운 노드를 부모 노드와 비교 후, 교환해서 힙의 성질을 만족시킨다.
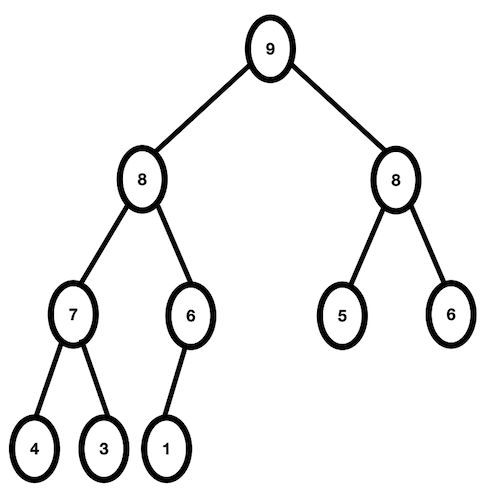
- 힙에 새로운 요소가 들어오면, 새로운 노드를 힙의 가장 마지막 노드에 이어서 삽입한다.
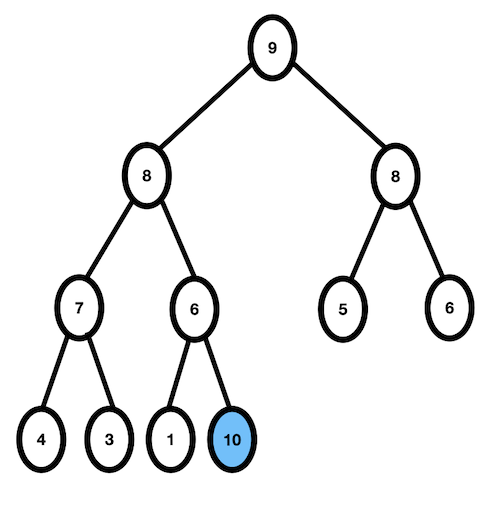
- 새로운 요소 10을 가장 마지막 위치에 삽입
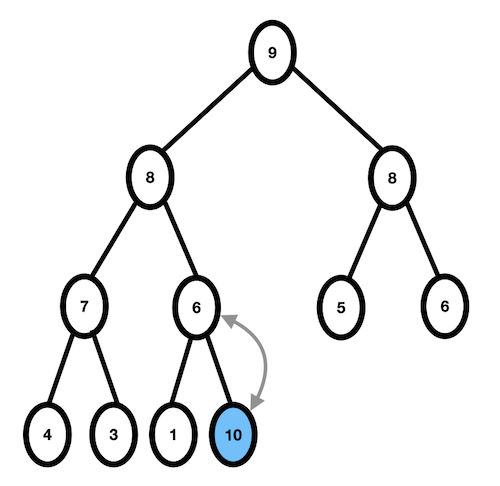
- 10과 부모인 6을 비교, 10 > 6 이므로 자리교환이 일어난다.
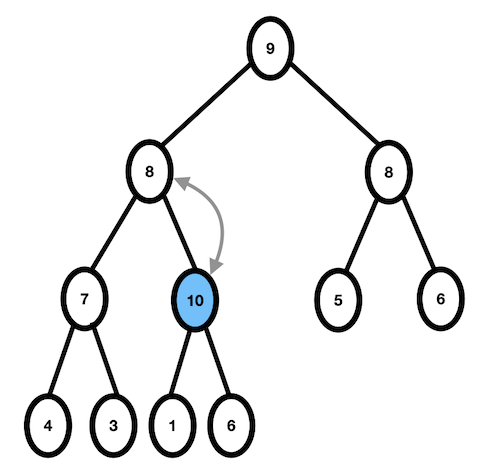
- 10과 그 위의 부모인 8을 비교, 10 > 8 이므로 자리교환이 일어난다.
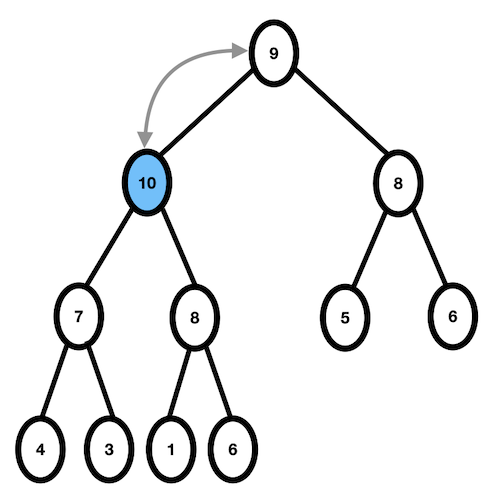
- 10과 그 위의 부모인 9를 비교, 10 > 9 이므로 자리교환이 일어난다.
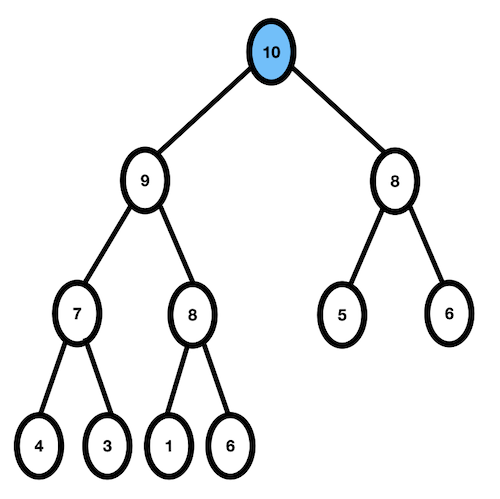
- 더 이상 비교할 대상이 없으므로 종료.
힙의 삭제
- 최대 힙에서 최대값은 루트 이므로, 루트 노드를 삭제한다.
- 삭제된 루트 노드에 힙의 가장 마지막 노드를 가져온다.
- 힙을 재구성한다.
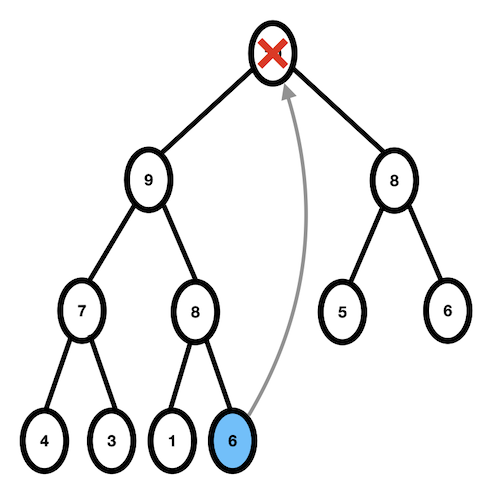
1. 최대값인 루트 노드 10을 삭제.
2. 빈 자리에 가장 마지막 노드인 6을 가져온다.
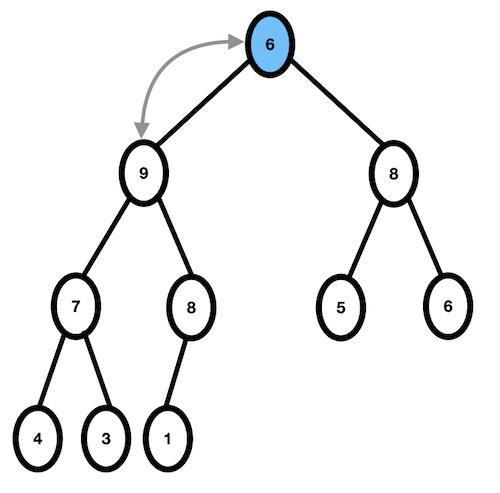
3. 6과 두 자식 노드 중 더 큰 값인 9를 비교, 9 > 6 이므로 자리교환이 일어난다.
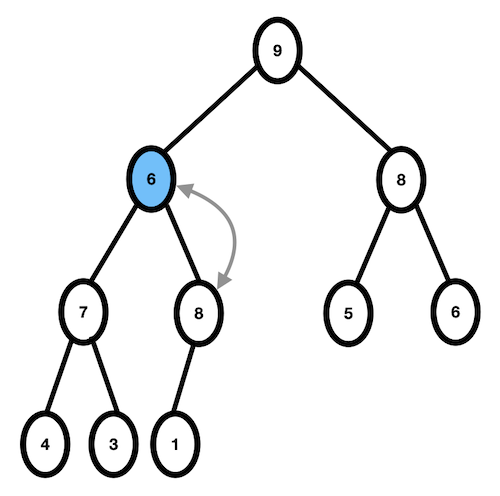
- 6과 두 자식 노드 중 더 큰 값인 8을 비교, 8 > 6 이므로 자리교환이 일어난다.
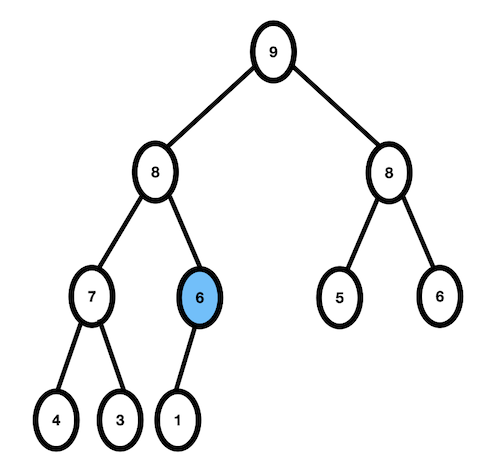
- 6보다 큰 자식 노드가 없으므로 종료한다.
2-5. 힙 구현 - Java 코드
public class Heap<T extends Comparable<T>> {
private ArrayList<T> items;
public Heap() {
this.items = new ArrayList<>();
}
/** 데이터 삽입 */
private void siftUp() {
int k = items.size() - 1;
while (k > 0) {
int p = (k - 1) / 2;
T item = items.get(k);
T parent = items.get(p);
if (item.compareTo(parent) > 0) {
// swap
items.set(k, parent);
items.set(p, item);
// move up one level
k = p;
} else {
break;
}
}
}
public void insert(T item) {
items.add(item);
siftUp();
}
/** 데이터 삭제 */
private void siftDown() {
int k = 0;
int l = 1;
while (l < items.size()) {
int max = l, r = l + 1;
if (r < items.size()) {
if (items.get(r).compareTo(items.get(l)) > 0) {
max++;
}
}
if (items.get(k).compareTo(items.get(max)) < 0) {
// switch
T tmp = items.get(k);
items.set(k, items.get(max));
items.set(max, tmp);
k = max;
l = 2 * k + 1;
} else {
break;
}
}
}
public T delete() throws NoSuchElementException {
if (items.size() == 0)
throw new NoSuchElementException();
if (items.size() == 1)
return items.remove(0);
T hold = items.get(0);
items.set(0, items.remove(items.size() - 1));
siftDown();
return hold;
}
public int size() {
return items.size();
}
public boolean isEmpty() {
return items.isEmpty();
}
public String toString() {
return items.toString();
}
}References
- https://gmlwjd9405.github.io/2017/10/01/basic-concepts-of-development-algorithm.html
- https://ko.wikipedia.org/wiki/힙(자료구조)
- 보요 시바타, 『자료구조와 함께 배우는 알고리즘 입문』, 이지스퍼블리싱(2018)
- 모든 이미지는 직접 그림
