10.1 선형 회귀
목적 : 하나 이상의 특성과 연속적인 타깃 변수 사이의 관계를 모델링하는 것
- 범주형 클래스 레이블이 아니라 연속적인 출력 값을 예측
10.1.1 단순 선형 회귀
단순 선형 회귀 : 하나의 특성(설명 변수 x)과 연속적인 타깃(응답 변수 y)사이의 관계를 모델링
y = w0 + w1x
해당 방정식으로 훈련 데이터셋이 아닌 새로운 샘플의 타깃 값을 예측
목적 : 특성과 타깃 사이의 관계를 나타내는 선형 방정식의 가중치를 학습하는 것
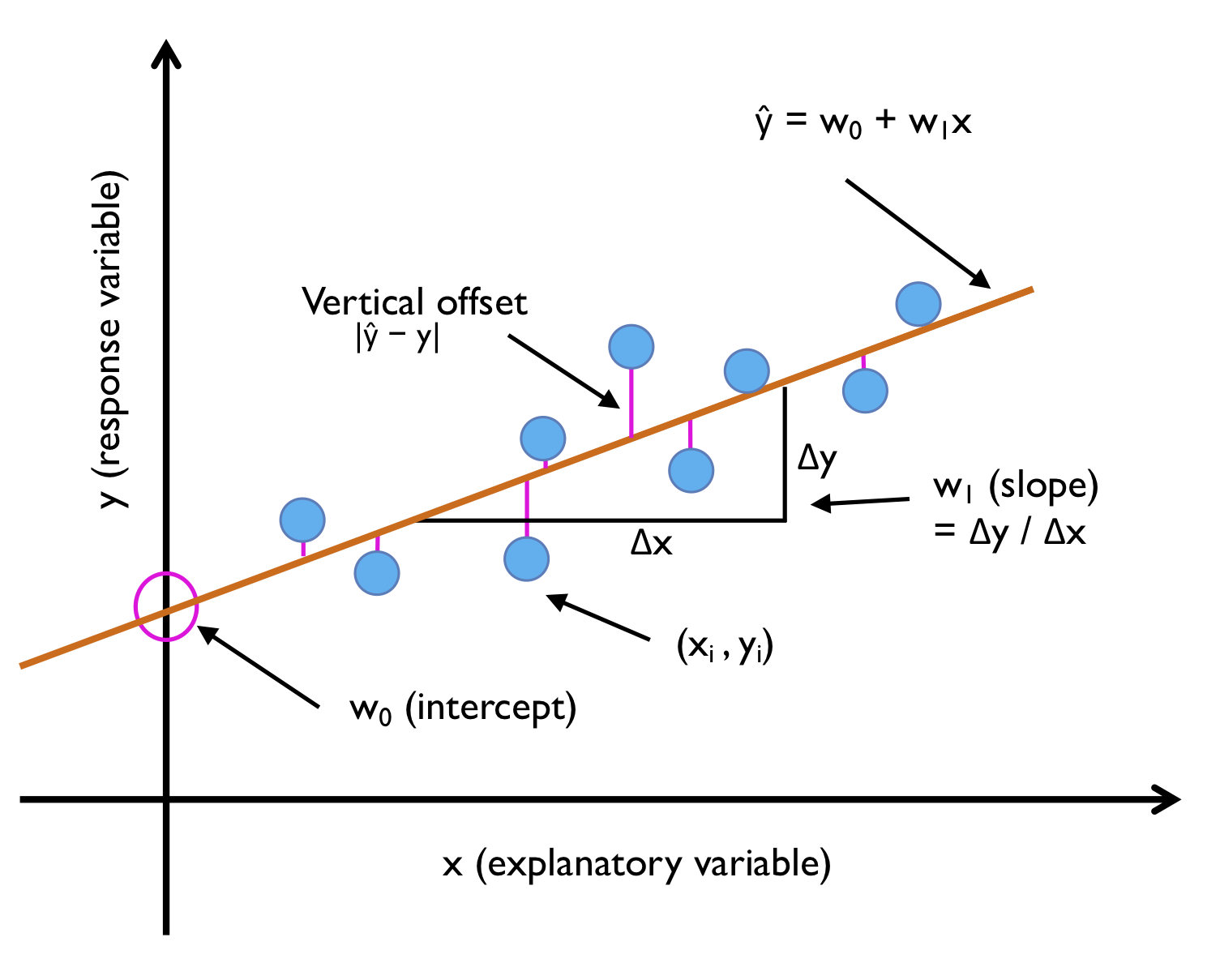
회귀 직선 : 데이터에 가장 잘 맞는 위의 그림과 같은 직선
오프셋(잔차) : 회귀 직선과 훈련 샘플 사이의 직선 거리
10.1.2 다중 선형 회귀
다중 선형 회귀 : 특성이 여러 개 있는 선형 회귀 모델
-> 다변량 회귀의 2차원 초평면을 시각화하는 좋은 방법이 없기 때문에 여기서는 단변량 회귀를 사용하여 하나의 특성을 가진 예제와 그래프를 다룸
(단변량 회귀와 다변량 회귀는 같은 개념과 평가 기법을 사용하여 모두 호환됨)
10.2 주택 데이터셋 탐색
주택 데이터셋 : 1978년에 해리슨과 루빈펠드가 수집한 보스턴 교외 지역의 주택 정보 (506개의 샘플)
- CRIM : 도시의 인당 범죄율
- ZN : 2만 5,000평방 피트가 넘는 주택 비율
- INDUS : 도시에서 소매 업종이 아닌 지역 비율
- CHAS : 찰스 강 인접 여부(강 주변=1, 그 외=0)
- NOX : 일산화질소 농도(10ppm당)
- RM : 주택의 평균 방 개수
- AGE : 1940년 이전에 지어진 자가 주택 비율
- DIS : 다섯 개의 보스턴 고용 센터까지 가중치가 적용된 거리
- RAD : 방사형으로 뻗은 고속도로까지 접근성 지수
- TAX : 10만 달러당 재산세율
- PTRATIO : 도시의 학생-교사 비율
- B : 10000(Bk - 0.63)2, 여기서 Bk는 도시의 아프리카계 미국인 비율
- LSTAT : 저소득 계층의 비율
- MEDV : 자가 주택의 중간 가격(1,000달러 단위)
-> 주택 가격(MEDV)을 타깃 값으로 삼음
-> 13개의 특성 중 하나 이상을 사용하여 이 값을 예측
10.2.1 데이터프레임으로 주택 데이터셋 읽기
read_csv 함수 : 주택 데이터셋을 읽어들이기 위한 함수로, 빠르기 때문에 텍스트로 저장된 CSV 형태의 파일을 다룰 때 사용하기 좋음
☑️DataFrame으로 데이터 불러오기☑️
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/rasbt/'
'python-machine-learning-book-3rd-edition/'
'master/ch10/housing.data.txt',
header=None,
sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()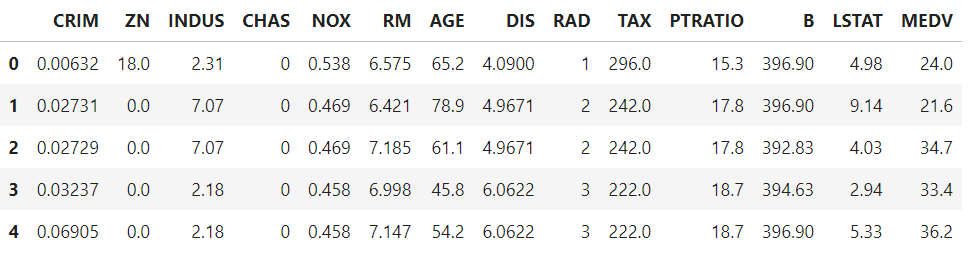
10.2.2 데이터셋의 중요 특징 시각화
탐색적 데이터 분석(EDA) : 머신 러닝 모델을 훈련하기 전에 첫 번째로 수행할 중요하고 권장되는 단계
-> EDA 그래픽 도구 : 이상치를 감지하고 데이터 분포를 시각화하거나 특성 간의 관계를 나타내는 데 도움
☑️산점도 행렬을 그려서 데이터셋에 있는 특성 간의 상관관계를 시각화☑️
- MLxtend 라이브러리 : 머신 러닝과 데이터 과학 애플리케이션에서 편리하게 사용할 수 있는 다양한 함수를 제공
conda install mlxtend
pip instal mlxtendimport matplotlib.pyplot as plt
from mlxtend.plotting import scatterplotmatrix
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
scatterplotmatrix(df[cols].values, figsize=(10, 8),
names=cols, alpha=0.5)
plt.tight_layout()
plt.show()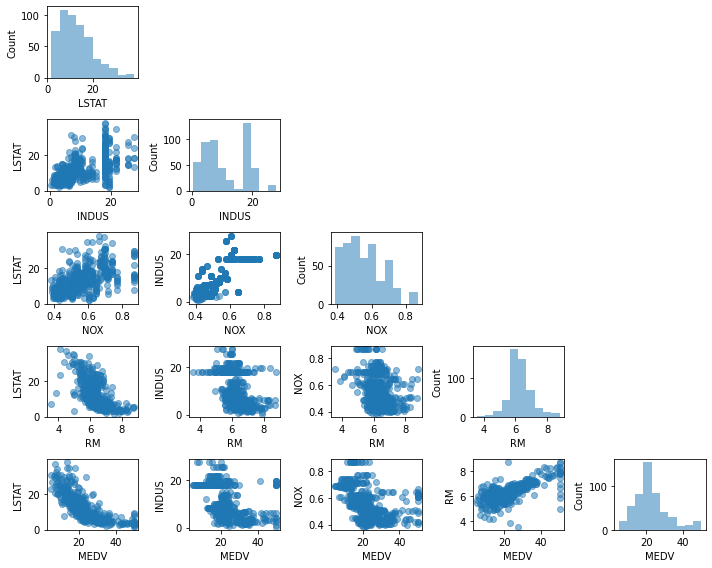
10.2.3 상관관계 행렬을 사용한 분석
상관관계 행렬 - 공분산 행렬과 밀접하게 관련, 직관적으로 생각하면 상관관계 행렬을 스케일 조정된 공분산 행렬로 생각 가능 -> 특성이 표준화되어 있으면 상관관계 행렬과 공분산 행렬이 같음
상관관계 행렬 - 피어슨의 상관관계 계수를 포함하고 있는 정방 행렬(피어슨의 r) -> 이 계수는 특성 사이의 선형 의존성을 측정
- 상관관계 계수의 범위 : -1 ~ 1
- r=1 : 두 특성이 완벽한 양의 상관관계를 가짐
- r=0 : 아무런 상관관계가 없음
- r=-1 : 완벽한 음의 상관관계를 가짐
- 피어슨의 상관관계 계수 : 단순히 두 특성 x와 y 사이의 공분산(분자)을 표준 편차의 곱(분모)로 나눈 것
corrcoef 함수 : 피어슨 상관관계 계수 구해주는 함수
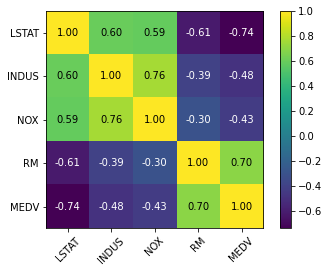
heatmap 함수 : 상관관계 행렬을 히트맵으로 나타냄
import numpy as np
from mlxtend.plotting import heatmap
cm = np.corrcoef(df[cols].values.T)
hm = heatmap(cm, row_names=cols, column_names=cols)
plt.show()