이 시리즈의 목표는 중고등학생 수준으로 각종 논문을 읽어보고 이해하는 것에 있습니다. 이를 통하여 점진적으로 전문 용어와 개념에 익숙해지고자 합니다. 따라서 자세한 부분에서 틀린 부분이 있거나 전문적이지 않을 수 있습니다. 필요한 부분은 따로 더 집중적으로 다룰 예정입니다. 또한 영어-한국어의 번역이 매끄럽지 않을 수 있습니다. 영어적 표현에 익숙해지는 과정으로 보기를 바랍니다. 논문의 완전한 번역보다는 이해를 위한 발최 의역을 기본으로 합니다.
알아야 할 간단한 정의
-
원핫 임베딩(one-hot embedding): 0과 1로 이루어진 데이터 표현방법. 각 위치는 속성에 해당하지 않음/해당함을 표시함.
-
메시지 전달 공식(message-passing formulation): 그래프 형식의 데이터에서 노드와 엣지를 따라 메시지를 생성하고 전달하여 새로운 메시지를 생성하는 방식
-
스위시 함수(Swish function)
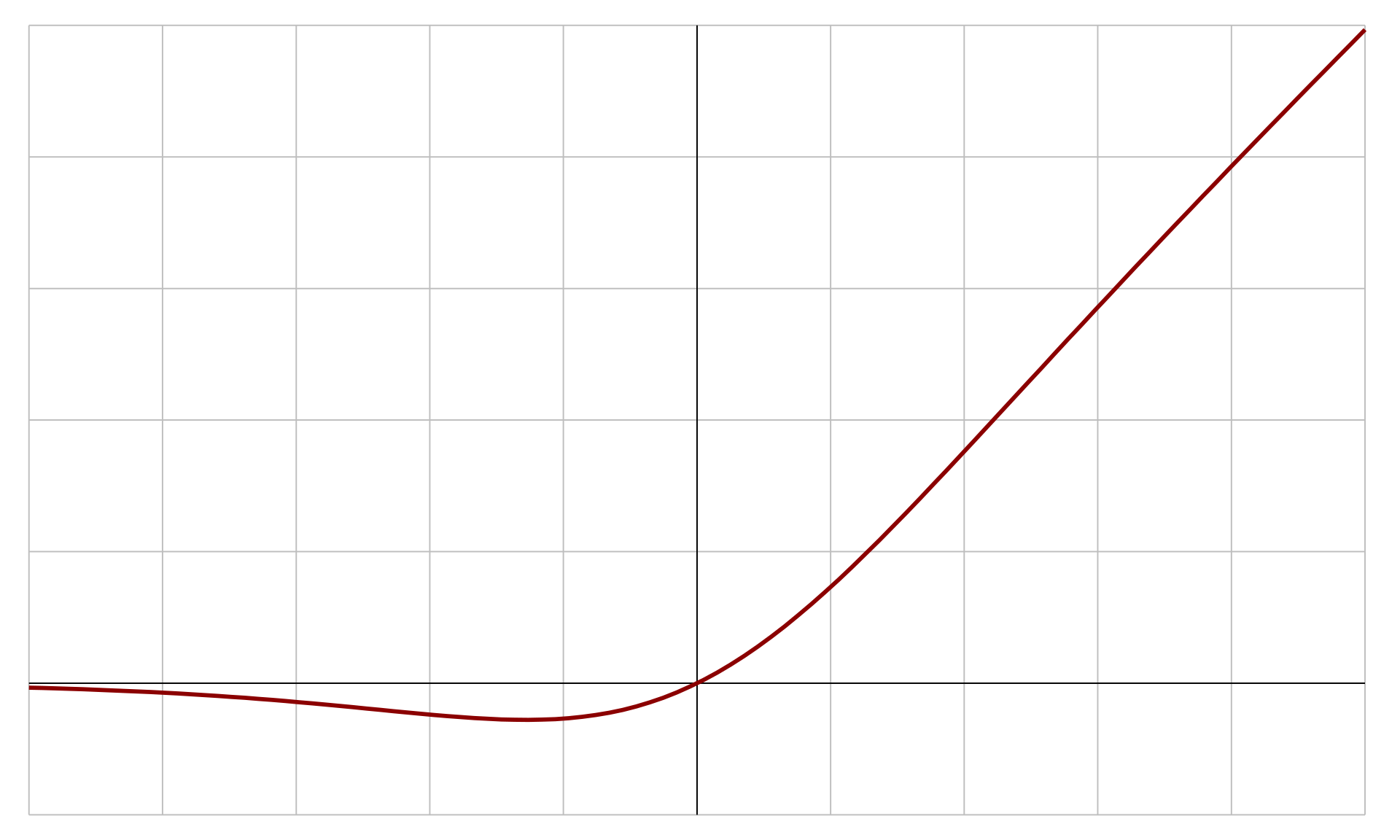source -
멀티 레이어 퍼셉트론(multilayer perceptrons (MLPs)): 레이어별로 여러개의 입력단자(퍼셉트론)을 생성하고 입력값에 대하여 각 단자별로 연산을 한다. 이러한 과정을 여러 레이어를 거치며 계산한다.
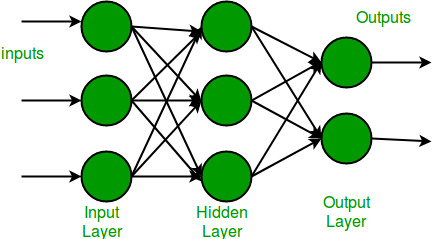source -
그래프 신경망 (graph neural networks (GNNs)): 그래프 구조를 가진 데이터를 학습하는 신경망
GNoME
GNoME 모델은 결정의 총 에너지를 예측하는 모델입니다. 입력은 원핫 임베딩을 통해 그래프로 변환됩니다. 메시지 전달 공식을 사용하고 얕은 MLP 활동함수로 스위시(swish) 함수를 사용함니다. 구조적 모델의 경우에는 정규화가 중요합니다. 기존의 유명한 구조를 수정하고 확장에 집중하여 작업하였습니다. 이를 통하여 성능의 개선을 이루었습니다.(28 -> 21 meV )
능동적 학습(active learning)
구조적으로, 구성 성분적으로 걸러진 후보들은 표준화 된 DFT 계산을 통하여 평가됩니다. 이렇게 생성된 자료를 기반으로 구조의 안정성을 검증하고, 후보 생성을 위한 추가 데이터로 사용됩니다. 6번의 능동적 학습동안 성능은 꾸준하게 향상되었습니다. 이를 통해 구조적 적중률 6%와 구성적 적중률 3%에서 시작하여 학습을 통해 80%와 33%으로 향상됩니다. 또한 완화된 구조에서 예측 오차도 11 meV 로 향상 되었습니다.
확장 법칙과 일반화(Scaling laws and generalization)
GNoME 모델의 성능은 데이터가 늘어날수록 거듭제곱 법칙처럼 개선되는 것으로 관측되었습니다. 이는 기존의 딥러닝의 신경확장법칙과 일치합니다. 이는 추가적인 발견으로 일반화를 개선할 수 있음을 의미합니다. 재료과학에서는 계속해서 데이터를 생성하고 안정적인 결정을 발견할 수 있고, 이를 사용하여 모델의 발전에 사용할 수 있습니다. 결정의 치환에서 무작위 검색을 사용하여 생기는 데이터를 훈련된 구조적 모델에 테스트하여 분포 외 작업에 대한 일반화를 입증했습니다. 이는 그림 1e에 나타나 있습니다. 이런 식으로 생겨난 데이터의 경우는 구조 파이프라인에서 생성된 데이터(치환으로 인해 최소값에 가까운 구조를 가지고 있음)에 비해 에너지가 높고 분포에서 벗어난 경우가 많습니다. 확장성에 대한 개선점이 관찰되었다는 것과 에너지 예측에 대한 일반적인 모델을 향한 발전이 있었다는 것에 의미가 있습니다.
