"3D Gaussian Splatting for Real-Time Radiance Field Rendering" - Gaussian Splatting의 시발점

3D reconstruction 3D rendering Gaussian Splatting 논문 논문 리뷰

사전 세 줄 요약

NeRF의 느린 Volumetric Rendering 대신, 수만 개의 3D Gaussian을 통해 장면을 표현하여 실시간 렌더링을 가능하게 했다.
각 Gaussian의 위치, 크기, 회전, 색, Opacity를 직접 최적화하고, 필요할 때 분할-복제하는 적응적 densification으로 고품질 Rendering을 가능케 한다.
GPU-friendly한 타일 기반 rasterization + visibility sorting으로 빠르게 투영하여, 1080p에서 30-100 FPS 이상의 실시간 렌더링과 SOTA급 품질을 달성하였다.

Introduction

NeRF (Neural Radiance Field)는 연속적인 장면을 표현하는 고품질의 Radiance Field 표현 방법이지만, Rendering에 필요한 Stocastic Sampling은 실시간성을 저해시키고 노이즈를 유발할 수 있다. 논문에서 예시로 나온 Mip-NeRF360의 경우, 48시간 학습을 한 후 0.0071 FPS의 속도를 보인다.

이는 Ray Marching 방식의 학습 및 최적화에서 기인한다. Ray Marching이란, 카메라 픽셀마다 광선을 쏴서, 그 광선이 지나가는 경로의 수 많은 점을 샘플링하고 색을 누적해 최종 픽셀 색을 정하는 과정을 의미한다. 각 샘플 위치에 대해 모두 NeRF MLP를 호출하고, Density와 Color 를 수십~수백 번 호출해야하는 구조를 가지므로 필연적으로 느려질 수 밖에 없다.

빠른 Radiance Field를 위한 연구도 존재하지만, 결국 품질과의 Trade-off 관계가 발생한다. 예로, InstantNGP 방법의 경우, 7분의 학습과 9.2FPS의 속도를 보였지만, 앞서 말한 Mip-NeRF 대비 비교적 낮은 PSNR (Peak Signal-to-noise ratio) 점수를 보인다.

본 논문은 좋은 퀄리티와 더불어 실시간 Rendering을 목표로 한다. 실시간을 위해, 연속적인 Volumetric field를 쓰는 대신, Scene을 수십만 개의 3D Gaussian primitive로 표현한다.

Gaussian 방식을 채택함으로써, Volumetric rendering과 동일한 수학적 $\alpha$ -blending이 가능하며 geometry를 따라 anisotropic ellipsoid로 변형되므로, 점 기반만큼이나 혹은 그 이상의 surface 표현이 가능하다.
Gaussian의 개수와 크길 계속 조절하는 방식의 Adaptive Density Control 기법을 통해 Compact하면서도 고품질의 Geometry 표현을 달성한다.
Gaussian은 화면에 투영하면 2D ellipse가 되는데, 이걸 빠르게 그리기 위해 최적의 래스터화 방법을 구축하였다.

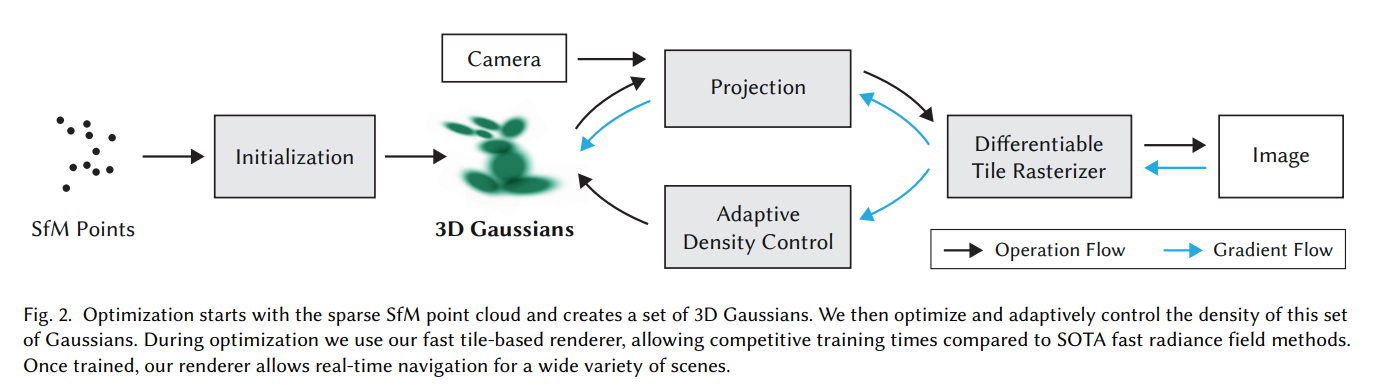
결론적으로, 이 논문은 Gaussian Splatting 기법을 제시함으로써, SOTA 수준의 3D Reconstruction Quality, 빠른 학습, 실시간 렌더링을 모두 달성한 연구로, Radiance Field 연구의 패러다임을 바꿨다고 볼 수 있다. 아래 Figure 2에서 전체 알고리즘의 Overview를 보인다.

Differentiable 3D Gaussian Splatting

3D Gaussian을 어떻게 미분 가능하게 만들어 최적화할 수 있게 만드는지 설명한다.
우선 왜 3D Gaussian인지부터 보자.

Volumetric처럼 부드러운 $\alpha$ blending이 가능해야 함.
그러나 NeRF처럼 ray marching 하지 않아야 함.
PointCloud처럼 fast rasterization도 가능해야 함.
Geometry에 자유롭게 맞춰 변형될 수 있어야 함.

이를 위한 최적 primitive가 Gaussian이다.

G(x) = \exp (-\frac{1}{2} (x-\mu)^{\top} \Sigma^{-1} (x - \mu))

위 수식이 3D Gaussian의 정의이며 여기서 $\mu$ 는 중심(Center)를, $\Sigma$ 는 Covariance matrix를 의미한다. 중심과 공분산을 가지는 하나의 Gaussian 자체가 부드러운 Volumetric blob의 역할을 하며 이것이 곧 "Surface Patch"의 역할을 한다.

Gaussian은 3차원 공간에선 타원체(Ellipsoid)지만, 카메라에서 보면 2D Ellipse footprint가 된다. 이를 위해 covariance 또한 view space에서 2D covariance로 바꿔주어야 한다. 그 식은 아래와 같다.

\Sigma^{\prime} = JW \Sigma W^{\top} J^{\top}

여기서 $W$ 는 World -> Camera 간의 Transform을, $J$ 는 Projection jacobian을 나타낸다. 이렇게 함으로써, Gaussian이 화면에서 얼마나 퍼져 보이는지, 어떤 방향으로 늘어져 있는지, 화면의 어떤 픽셀에 영향을 미치는지 계산할 수 있게 된다.

당연히 최적화 한다하면, 3차원 Covariance $\Sigma$ 를 최적화 하는 시도를 하겠지만, Gradient Descent로 $\Sigma$ 의 6개 요소를 직접 Optimize하면 Gradient Explosion, Invalid covariance가 생기고 matrix가 비대칭일 될 수 있다. 그래서 논문은 Covariance를

\Sigma = RSS^{\top}R^{\top}

이렇게 파라미터화 한다. 여기서 $S$ 는 Scaling vector로 Gaussian Ellipsoid의 세 축 길이를, $R$ 은 Rotation matrix로 Gaussian의 기울기와 orientation을 내포한다. 또한 Quaternion normalize로 valid rotation을 보장하는데, 이렇게 함으로써 $\Sigma$ 는 무조건 valid covariance가 되며 최적화가 안정화 된다.

Optimization with Adaptive Density Control of 3D Gaussians

이번 절에선 Gaussian Splatting 파라미터를 최적화하는 과정과 Adaptive 하게 제어하는 방법을 소개한다. 먼저 최적화 해야하는 Gaussian의 파라미터는 다음과 같다.

위치 $p$ , Gaussian의 중심을 말하며 Geometry를 결정한다.
공분산 $Sigma$ , Scale과 Valid Rotation 그리고 Anisotropic을 Geometry에 맞게 변형
불투명도(투명도) $\alpha$ , 추후 Gaussian이 유지될지 삭제될지 결정한다.
색상 계수 $c$

이 네 가지를 렌더링 -> loss 비교 -> gradient update로 최적화 해야한다.

여기서 학습 루프는 다음과 같은 순서로 진행된다.
1. Training view (카메라 시점) 선택
2. 현재 Gaussian들을 Rasterization으로 rendering
3. Ground truth 이미지와 비교
4. Gradient로 Gaussian 파라미터 업데이트

사용되는 Loss function은 아래와 같다.

L = (1-\lambda)L_1 + \lambda L_{D-SSIM}

학습을 통해, Gaussian의 위치-크기-회전-색-투명도 모두를 loss 기반으로 최적화하여 장면을 점점 정확하게 표현하는 radiance field로 만든다.

Density control 단계는 Gaussian의 밀도를 자동으로 조절하여 다양한 구조를 표현하게하고, 효율성을 확보하게하는 단계이다. 크게 Clone/Split/Prune 매커니즘으로 나눠진다.

Clone : 작은 Gaussian들이 Geometry가 부족한 곳에 있을 때를 말한다. Gaussian이 작고 View-space positional gradient가 클 때를 조건으로 하며, Gaussian을 복제한 후 Gradient 방향으로 약간 이동하여 새로운 Gaussian을 복제한다.
Split : 큰 Gaussian이 복잡한 구조를 덮고 있는 것을 말한다. Gaussian이 크고 Gradient도 큰 경우를 말하며, 상세히 나눠야한다는 것을 의미한다. 이럴 땐 Gaussian을 쪼개어 큰 Gaussian이 지나치게 넓게 덮는 현상을 방지하고 섬세함을 확보한다.
Prune : Opacity가 거의 투명한 경우르 ㄹ말하며, 해당 포인트를 삭제함으로써, Compact함과 메모리 효율을 증가시킨다.

Fast Differentiable Rasterizer for Gaussians

이 Section에선 실시간을 위한 방법에 대해 논의한다.

기존의 NeRF처럼 Ray Marching 기법을 쓰면 실시간성을 달성할 수 없다. 실시간성을 위해선 다음과 같은 rasterizer가 필요하다.

화면 전체 Gaussian을 Depth 순으로 정렬
Per-pixel 정렬은 피해야함.
Per-Gaussian 또한 비효율적, Gaussian이 여러 픽셀에 영향을 주므로 다시 Sorting이 필요

따라서, 해당 방법은 tile-based rasterization을 제시한다. 화면을 16 $\times$ 16으로 나누도, 각 tile에 어떤 Gaussian이 영향을 주는지 정리한 뒤, 그 tile 안에서만 depth-sort하여 각 tile마다 depth-sorted Gaussian 목록을 얻고, 타일 단위로 GPU thread block 하나가 처리하는데, tile에 속한 Gaussian들을 front-to-back으로 순회하며 투명도와 색, 그리고 투과율을 계산한다. 이 $\alpha$ blending은 NeRF의 volumetric rendering 공식과 정확히 동일한 방식이다.

C = \Sigma_i T_i \alpha_i c_i, T_i = \prod_{j<i}(1-\alpha_j)

이때, $\alpha$ -blending 자체가 누적 구조라 역전파가 까다롭지만, 이 논문은 중간값을 누적하지 않고 backward에서 재계산을 하여 메모리를 절약한다. 결론적으로 forward에선 최종 투과율만 저장하고, backward에선 prefix product를 재구축하며 tile 단위로 back-to-front 순서로 gradient 계산을 수행한다.

결과

결과에 대해 간단히 논의하자면, SOTA 품질을 달성하고 실시간 렌더링을 가능하게 하였다. 또한 학습 또한 빨라 최적화 과정에 5~30분 이내로 완료 된다. 특히, Anisotropic Gaussian 덕분에 경계 표현이 뛰어나단 장점이 있으며 Ablation Study를 통해서도 모든 구조가 전체 결과에 중요한 기여를 함을 보인다.

하지만, 여전히 논문에선 몇가지 한계점을 논의한다.

메모리 소비가 크다 : 수 많은 파라미터와 수 많은 Gaussian 수로 인해 메모리를 많이 차지함.
Geomtery Robustness가 제한적 : Geometry 자체는 implicit surface가 아니기에, 완전히 waterlight mesh를 표현할 수 없다. 즉 특정 개체 및 표면에 대해 수식적으로 명확한 정의를 내릴 수 없다.
반투명/Complex lighting에는 제한적이다.
훈련 뷰 밖의 Extrme extraploation에는 제한적
Static scene assumptioni

이로운

Robotics Engineer / https://www.linkedin.com/in/roun-lee-5503382b6/

이전 포스트