T-검정(T-test)
T-검정의 정의
T-검정은 모집단의 분산이나 표준편차를 알지 못할 때, 표본으로부터 추정된 분산이나 표준편차를 이용하여 두 모집단의 평균의 차이를 알아보는 검정 방법이다.
집단의 수는 최대 2개까지 비교 가능하며, 3개 이상인경우 분산분석(ANOVA)를 사용한다.
t-test의 목적
두개의 집단이 같은지 다른지 비교하기 위해
T-검정의 가정
- 종속변수가 양적 변수일 때
- 모집단의 분산이나 표준편차를 알지 못할 때
- 모집단의 분포가 정규분포일 때
T-검정의 조건
- 독립성 : 독립변수의 그룹 군은 서로 독립적 이어야 한다.
❌대응표본일 경우 : 대응표본 T-검정 실행 - 정규성 : 독립변수에 따른 종속변수는 정규분포를 만족해야한다.
❌정규분포가 아닐 경우 : Mann-Whitney test 실행 - 등분산성 : 독립변수에 따른 종속변의 분포의 분산은 유사한 값을 가진다.
❌분산이 서로 다를 경우 : 자유도를 수정한 독립표본 T-검정 실행
대응 표본의 T-검정(Paired T-test)
실험 이전의 집단과 실험 이후의 집단이 동일한 집단인 경우 사용하는 검정으로 한 사람이 처리 이전과 이후 각 1번씩 측정을 해서 사전/사후를 비교하는 것을 말한다.
모집단이 1개인 경우이다.
쌍을 이룬 두 변수 간에 차이의 평균이 0인지를 검정한다.
대응표본과 독립표본의 차이
| 독립표본 T 검정 | 대응표본 T 검정 |
|---|---|
| 조사대상 개체가 다름 | 조사대상 개체가 같음 |
| 두 범주의 표본 숫자가 다를 수 있음 | 표본 숫자가 같음 |
| 다른 집단을 비교 | 전후 개념이 있는 경우가 많음 |
[출처]http://www.incodom.kr/이론_및_T검정
양측검정(two-tailed test), 단측검정(one-tailed test)
양측검정
단측검정
오른쪽꼬리(upper tail)
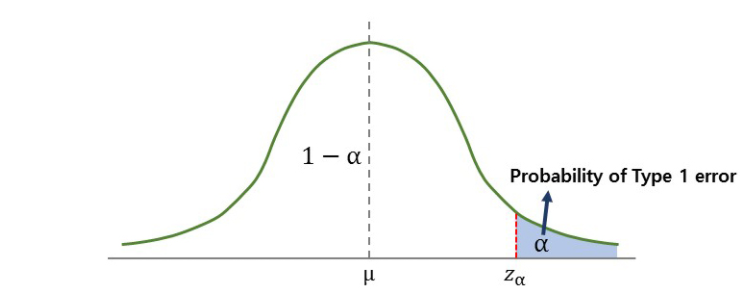
왼쪽꼬리(lower tail)
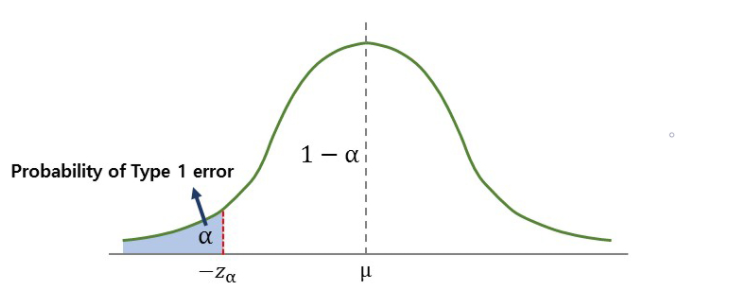
[이미지출처]https://m.blog.naver.com/mykepzzang/220886418140
검정 통계량(Test Statistic) -> (t-value)
통계적 가설의 진위 여부를 검정하기 위해 표본으로 부터 계산하는 통계량
검정통계량의 의미
두 평균값에 대한 차이와 오류를 의미
표본 평균 차이의 통계적 지표
= 차이 불확실도
검정 통계량 식
표본 평균 차이의 통계적인 지표 =
