[TIL] 21.05.27 K-means cluster의 K값 구하기

1. 엘보우 기법 (Elbow method)

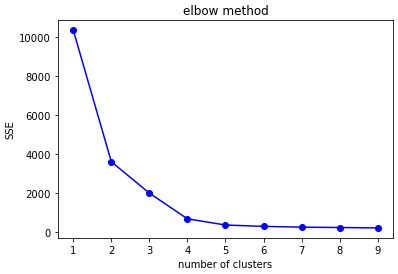
SSE(Sum of squred error)값을 클러스터의 개수를 두고 비교를 한 그래프를 통해 급격한 경사도를 보이다가 완만한 경사를 보이는 SSE값을 보이는 부분(팔꿈치)에 해당하는 클러스터를 선택하는 기법을 통해 최적의 K값을 선택할 수 있다.

$SSE = \sum_{i=1}^n(y_i - \hat{y_i})^2$

# 엘보우 기법 (오차제곱합의 값이 최소가 되도록 결정하는 방법)
def elbow(data, length):
    sse = [] # sum of squre error 오차제곱합
    for i in range(1, length):
        kmeans = KMeans(n_clusters=i)
        kmeans.fit(data)
        # SSE 값 저장
        sse.append(kmeans.inertia_)
    plt.plot(range(1, length), sse, 'bo-')
    plt.title("elbow method")
    plt.xlabel("number of clusters")
    plt.ylabel("SSE")
    plt.show()
elbow(points, 10)

out:

2. 실루엣 기법 (Silhouette method)

• 실루엣 분석은 각 군집 간의 거리가 얼마나 효율적으로 분리 돼있는지를 나타냄

• 효율적으로 잘 분리 됐다는 것은 다른 군집과의 거리는 떨어져 있고 동일 군집끼리의 데이터는 서로 가깝게 잘 뭉쳐 있다는 의미

  $s^{(i)} = {b^{(i)} - a^{(i)} \over max({a^{(i)},b^{(i)}})}$

  a(i) = 데이터 응집도를 나타내는 값
  b(i) = 클러스터 간의 분리도

실루엣 계수 값은 0 ~ 1의 값을 가진다. 1에 가까울 수록 클러스터의 갯수에 따른 데이터는 군집과 멀리 떨어져 있다는 뜻이고, 0에 가까울수록 근처의 군집과 가깝다는 뜻이다.
실루엣 계수는 1에 가까울수록 최적화가 잘 되어있다라고 판단할 수 있다.

다음의 코드는 ariz1623님의 블로그를 참조했습니다.

# 실루엣 기법
def visualize_silhouette(cluster_lists, X_features): 

    from sklearn.datasets import make_blobs
    from sklearn.cluster import KMeans
    from sklearn.metrics import silhouette_samples, silhouette_score

    import matplotlib.pyplot as plt
    import matplotlib.cm as cm
    import math

    # 입력값으로 클러스터링 갯수들을 리스트로 받아서, 각 갯수별로 클러스터링을 적용하고 실루엣 개수를 구함
    n_cols = len(cluster_lists)

    # plt.subplots()으로 리스트에 기재된 클러스터링 수만큼의 sub figures를 가지는 axs 생성 
    fig, axs = plt.subplots(figsize=(4*n_cols, 4), nrows=1, ncols=n_cols)

    # 리스트에 기재된 클러스터링 갯수들을 차례로 iteration 수행하면서 실루엣 개수 시각화
    for ind, n_cluster in enumerate(cluster_lists):

        # KMeans 클러스터링 수행하고, 실루엣 스코어와 개별 데이터의 실루엣 값 계산. 
        clusterer = KMeans(n_clusters = n_cluster, max_iter=500, random_state=0)
        cluster_labels = clusterer.fit_predict(X_features)

        sil_avg = silhouette_score(X_features, cluster_labels)
        sil_values = silhouette_samples(X_features, cluster_labels)

        y_lower = 10
        axs[ind].set_title('Number of Cluster : '+ str(n_cluster)+'\n' \
                          'Silhouette Score :' + str(round(sil_avg,3)) )
        axs[ind].set_xlabel("The silhouette coefficient values")
        axs[ind].set_ylabel("Cluster label")
        axs[ind].set_xlim([-0.1, 1])
        axs[ind].set_ylim([0, len(X_features) + (n_cluster + 1) * 10])
        axs[ind].set_yticks([])  # Clear the yaxis labels / ticks
        axs[ind].set_xticks([0, 0.2, 0.4, 0.6, 0.8, 1])

        # 클러스터링 갯수별로 fill_betweenx( )형태의 막대 그래프 표현. 
        for i in range(n_cluster):
            ith_cluster_sil_values = sil_values[cluster_labels==i]
            ith_cluster_sil_values.sort()

            size_cluster_i = ith_cluster_sil_values.shape[0]
            y_upper = y_lower + size_cluster_i

            color = cm.nipy_spectral(float(i) / n_cluster)
            axs[ind].fill_betweenx(np.arange(y_lower, y_upper), 0, ith_cluster_sil_values, \
                                facecolor=color, edgecolor=color, alpha=0.7)
            axs[ind].text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
            y_lower = y_upper + 10

        axs[ind].axvline(x=sil_avg, color="red", linestyle="--")

visualize_silhouette([2, 3, 4, 5, 6], points)

out:

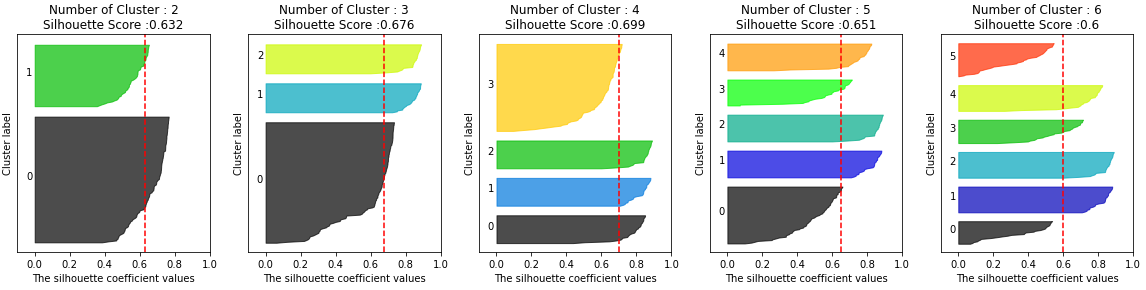
클러스터 개수가 최적화 되어어 있다면 분리도의 값은 커지고, 응집도의 값은 작아지기 때문에 실루엣 계수는 1에 가까워 진다.

결국 실루엣 계수가 1에 가까울 수록 클러스터의 갯수가 최적화 되어있다고 판단할 수 있다.

위의 그래프를 통해 확인했을 때 클러스터의 갯수가 4개일 때 제일 실루엣 계수가 높은 것을 볼 수 있다.

엘보우 기법, 실루엣 기법 참고 : https://m.blog.naver.com/samsjang/221017639342

실루엣 기법 참고 : https://ariz1623.tistory.com/224